Спиральный вариант Периодической системы элементов

Кажется, о периодической системе химических элементов Д.И.Менделеева, о законе периодичности, о ядерной периодичности сказано и написано столько, что добавить что-то новое невозможно. Но это не так.

На сегодняшний день известно уже несколько сотен различных графических и спиральных вариантов системы элементов. Появление каждого из них было обусловлено различными причинами. Большинство вариантов исходило от химиков-практиков и физиков-атомщиков: химические свойства и особенности элементов и их соединений - с одной стороны, с другой - квантовые характеристики атомных и ядерных систем. В предлагаемой работе излагается радианный принцип построения нуклонных оболочек атомного ядра, приводится новый спиральный вариант Периодической системы химических элементов, а также делается попытка дать новое толкование Периодического закона Д. И. Менделеева.

К варианту Периодической системы, который приводится в данной работе, автор пришел от найденной им ранее модели частицы материи. Автор рассматривает частицу материи не как чрезвычайно малый объект с определённым электрическим зарядом или без него, а как некое возбуждение в материальной среде (физическом вакууме) вроде радиальных осцилляций плотности (дыхание вакуума). Такой подход заставил иначе взглянуть на механизмы связи подобных частиц-возбуждений в атомных системах. Осциллирующая природа частиц материи определила и механизм связи частиц между собой, который также носит периодический колебательный характер. Частица-возбуждение есть устойчивое энергоёмкое образование в среде, порождающее вокруг себя постоянное волновое поле. Механизм сильного взаимодействия в ядерной системе, как известно, объясняется мезонным обменом между нуклонами. С точки зрения автора, такому мезонному обмену можно дать иное толкование и назвать этот процесс мезонной шнуровкой. Только в качестве обменного мезона здесь выступает не частица - мезон, а напряженность волнового поля в известных точках противостояния частиц-возбуждений. Когда движения нескольких частиц согласованы, допустим, по фазе углов орбитальных моментов, то связь между частицами будет устойчива и энергетически выгодна. Когда же движение частиц рассогласуется в результате каких-либо внешних воздействий, то связь нарушается и система распадается или претерпевает изменения.

Новая формулировка Периодического закона Д. И. Менделеева будет звучать примерно так: свойства химических элементов и их соединений обусловливаются периодической упорядоченной формой движения атомных частиц элементов и нарушением этой упорядоченной формы движения вследствие присоединения, отсоединения или перегруппировки частиц.

По общепринятым воззрениям спины нуклонов в ядерных оболочках кратны полуцелым значениям, а орбитальные моменты складываются в результирующий спин и орбитальный момент ядра.

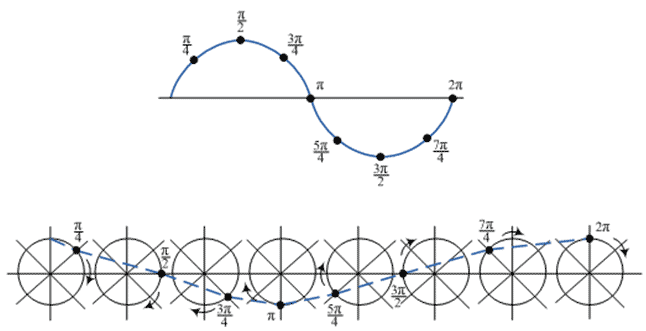
Рис. 1

Однако зададим себе вопрос: если заполненная нуклонами ядерная оболочка есть устойчивое образование и вся ядерная система устойчива, то могут ли здесь частицы двигаться хаотически, рассогласованно, не подчиняясь никакому принципу? Ответ однозначен - нет, не могут. Хаотичность движения нуклонов и устойчивость ядерной оболочки несовместимы. Только порядок и согласованность в движениях нуклонов обусловливают устойчивость ядерной оболочки и системы в целом. Согласование движений частиц в оболочке происходит по фазе углов орбитальных моментов нуклонов. Фаза угла здесь выражается через величину π радиан. Если в отдельно взятой ядерной оболочке, состоящей, предположим, из 8 нуклонов, каждая из частиц совершает периодическое орбитальное движение, графически изображаемое синусоидой (Рис. 1), то получается, что фаза орбитального момента каждого нуклона в любой момент времени будет кратна π/4 радиан. Складываясь вместе, фазы орбитальных моментов образуют одну волну с суммарным значением фазы 2π радиан. То есть в каждый момент времени значение фазы орбитального момента каждого нуклона в ядерной оболочке должно соответствовать известной величине, кратной π. Это справедливо и для оболочек, состоящих из двух нуклонов, где значение фазы орбитального момента каждой частицы в любой момент времени кратно целочисленному значению (π), и для оболочек из четырёх нуклонов, где значение фазы каждой частицы кратно полуцелому значению (π/2) (Рис. 2).

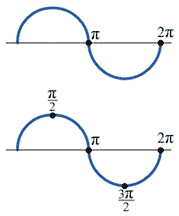
Рис. 2

Всё только что сказанное прямо следует из идей Луи де Бройля о волновой природе частиц материи и волновом характере их движения. Согласно одному из положений теории де Бройля, устойчивость электронной орбиты в атоме обусловливается целочисленностью электронных волн, укладывающихся на этой орбите (Рис. 3). В переосмысленном виде это же положение относится, по-видимому, и к ядерным оболочкам.

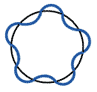
Рис. 3

Изложенный взгляд на причину устойчивости ядерной оболочки, как следствие согласованного, упорядоченного движения частиц, приводит к выводу о необходимости существования в оболочке дробных значений орбитальных моментов нуклонов. Рассмотрим полученный вывод на ядерных системах атомов химических элементов.

Так как ядро атома водорода состоит из одного нуклона, то говорить о существовании у этого нуклона орбитального момента не приходится, его просто нет. Орбитальный момент появляется у единственного нуклона тогда, когда он соединяется с ещё одним нуклоном, образуя вместе тяжелый водород - дейтерий. Значение фазы орбитального момента каждого нуклона в любой момент времени в данном случае будет кратно π радиан и направление моментов будет параллельным, а спины нуклонов будут кратны полуцелым значениям и антипараллельны. В итоге общий орбитальный момент дейтерия равен 2π радиан, а спин равен нулю (Рис. 4).

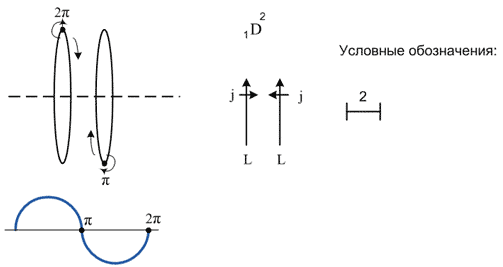
Рис. 4

В ядре атома гелия, состоящем из четырёх нуклонов, значение фазы орбитального момента каждой частицы в любой момент времени кратно π/2 радиан, что в сумме даёт величину 2π (Рис. 5). Согласованное по фазе орбитальных моментов движение четырёх нуклонов образует одну устойчивую волну - ядерную оболочку (группу). Целочисленность и чётность π радиан ядра атома гелия обусловливают его инертные свойства. У других инертных газов суммарное значение π орбитальных моментов также чётно и целочисленно. Именно чётность и целочисленность π радиан является мерой инертности химических элементов и их соединений.

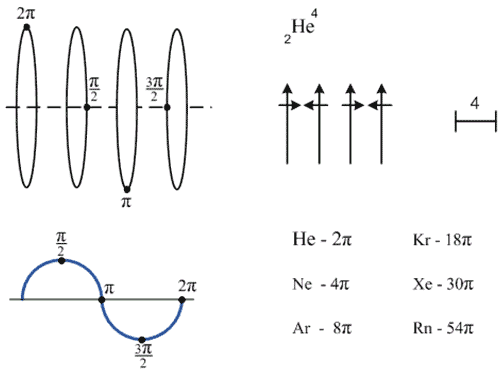
Рис. 5

Однако здесь может возникнуть вопрос: свойства химических элементов определяются всё же количеством валентных электронов на внешней электронной орбитали, но почему же здесь свойства элементов связываются сразу с характером движения ядерных частиц, а где электроны? Вопрос сложный и однозначного ответа у автора нет. Не исключено, что в данном случае имеет место строгая корреляция или полное соответствие в характере движения ядерных частиц и электронов, а также полное соответствие в последовательности заполнения ядерных и электронных оболочек. Так что, когда говорится о заполнении ядерных оболочек, речь идёт и о заполнении оболочек электронных. С другой стороны, автору с некоторых пор само существование электронных оболочек кажется весьма проблематичным. Не выдаём ли мы за эти электронные оболочки нечто другое?

Итак, активные химические свойства начинают обнаруживаться у элементов, когда к устойчивой группе ядерной оболочки инертного газа присоединяются новые нуклоны, вносящие в согласованное движение частиц дополнительное возмущение, иначе, вносящие асимметрию. Но присоединение нуклонов идёт не путём прямого прибавления их к устойчивой конфигурации инертного газа, а несколько иначе. Присоединение нуклона возможно лишь с добавлением к тому же ещё одной (для 3 и 4 периодов системы химических элементов) и двух (для 5, 6, 7 периодов) устойчивых групп из восьми частиц. Это даёт возможность отдельным нуклонам свободно спариваться с нуклонами устойчивой дополнительной группы. На Рис. 6 приведён пример заполнения второй оболочки второго периода системы химических элементов. Заполнение, а точнее, присоединение нуклонов к первой оболочке идёт с определённой последовательностью. При чётном количестве частиц вновь застраивающейся оболочки они располагаются симметрично относительно правой и левой части первой восьминуклонной группы. Представления о квантовых ячейках, которые, как известно, поочерёдно заполняют электроны на атомных орбиталях, здесь получают вполне наглядное толкование. Когда число нуклонов достигнет восьми, они образуют новую устойчивую оболочку с суммарным значением углового момента 2π радиан. Орбитальные моменты нуклонов в оболочке направлены параллельно, а спины соединяются попарно и антипараллельно. На Рис. 7 приведён порядок заполнения ядерных оболочек со второго по седьмой периоды.

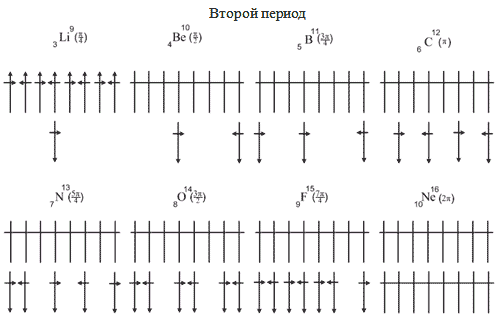
Рис. 6

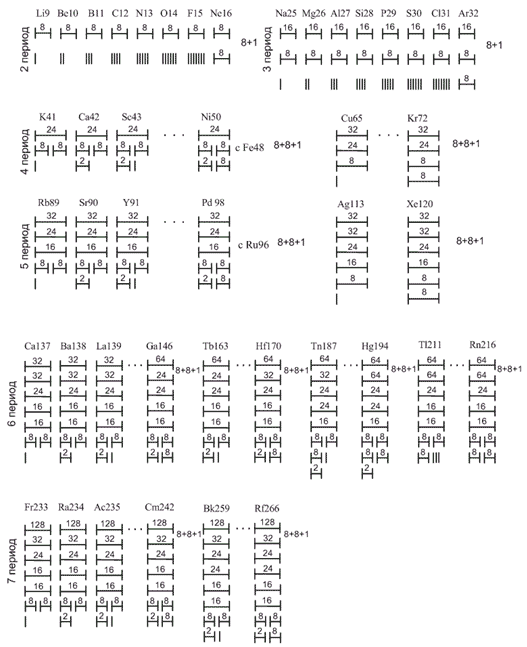
Рис. 7

Такой радианный принцип построения нуклонных оболочек ядра позволяет изобразить Периодическую систему химических элементов в виде правильной развивающейся спирали (Рис. 8). К тому же, у большинства химических элементов происходит изменение принятых значений относительных атомных масс. Однако следует заметить, что у 33 элементов системы найденные подобным образом массы точно совпадают с величинами масс наиболее стабильных изотопов этих элементов. На Рис. 9 они выделены рамкой (Селинов И.П., "Изотопы", изд. Наука, М., 1970 г.). Приведённые новые значения атомных масс являются как бы строгими, чистыми значениями, теоретическими. В реальной же природе, конечно, такой строгости и чистоты мы не имеем, а если и имеем, то весьма редко.

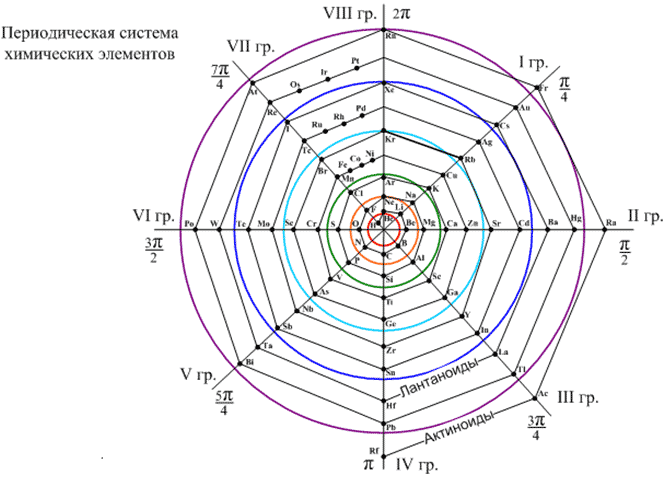
Рис. 8

Всё изложенное выше позволяет иначе посмотреть на природу так называемого ядерного заряда, который, как известно, определяет свойства химических элементов. Представления о заряде ядра здесь, по существу, заменяются представлениями о пери-одических коллективных движениях ядерных частиц и их возмущениях. Соединение различных атомов в молекулу можно попытаться объяснить теперь не электростатическими взаимодействиями зарядов, а стремлением этих атомов к получению чётного и (или) целочисленного значения радиан орбитальных моментов на внешней оболочке, иначе, к полной согласованности движений всех частиц, и, следовательно, к получению минимума общей энергии атомной или молекулярной системы. Так называемый фактор энергетической выгоды может быть понят только с точки зрения резонансного взаимодействия, условия устойчивой резонансной связи частиц-осцилляторов. Энергетический фактор атомной системы здесь тесно переплетается с геометрическим, а именно - с симметрией.

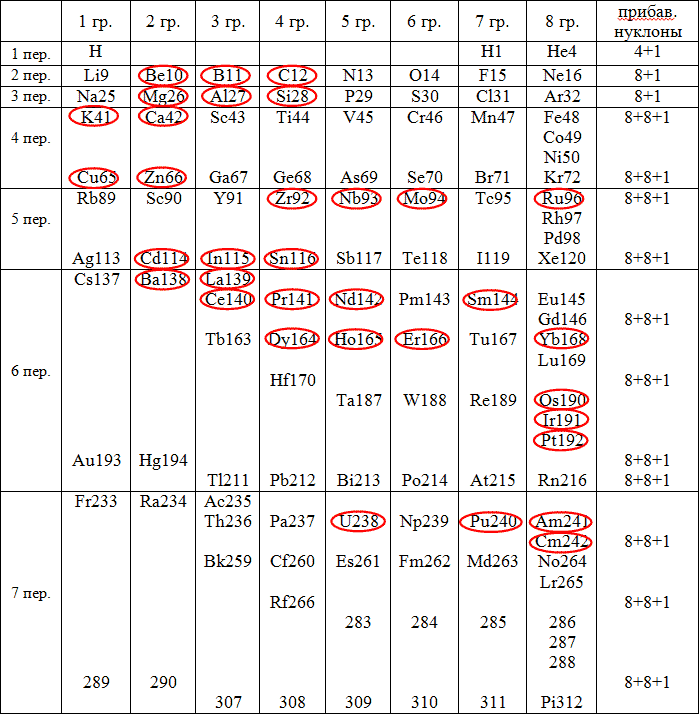
Рис. 9 Периодическая система химических элементов. Теоретические значения атомных масс

Выше уже говорилось, что мерой инертности и стабильности элемента или химического соединения является целочисленность и чётность радиан, а в целом ряде случаев (особенно соединений) просто целочисленность. Это легко проверить. Возьмём молекулу какого-нибудь устойчивого соединения, сложим значения π радиан орбитальных моментов соответствующих им атомов (см. Рис. 8), и получим в результате целое число π:

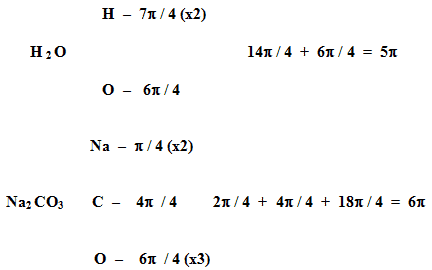
Все устойчивые молекулярные соединения, встречающиеся в природе и находящиеся в нормальных условиях, т.е. при отсутствии критических для них температур, давлений и электрических напряжений, имеют в сумме целочисленное значение π радиан орбитальных моментов. Наряду с ними существуют соединения с дробными значениями π радиан. Как правило, эти соединения неустойчивы: они или быстро распадаются, или образуют новые связи с другими элементами. Относительно устойчивые соединения с целочисленным значением π радиан, попав в критические для себя условия, также распадаются или образуют новые связи. Что, в общем, и составляет сущность химических реакций.

На целочисленность π радиан автором было проверено множество устойчивых молекулярных соединений. Проверка проводилась путём подсчёта, пример которого приведён выше. Все молекулярные соединения вполне отвечают правилу устойчивости. У подавляющего большинства из них (примерно 90 %) π радиан не только целочисленно, но и чётно. Однако здесь была трудность с химическими элементами, проявляющими различную валентность и, следовательно, которые в каждом случае должны быть отнесены к различным группам системы элементов. Так, например, сера проявляет валентность 2, 4, 6 и, следовательно, в каждом случае должна быть отнесена соответственно к группам: π/2, π, 3π/4. На вопрос: почему химический элемент, отнесённый к строго определённой группе системы, проявляет различную валентность? - можно было бы ответить так. Нуклоны вновь застраивающейся ядерной оболочки способны образовывать между собой двух- и четырёхчастичные устойчивые группы со значением фазы углового момента соответственно π и π/2 радиан. Оставшиеся вне этой группы нуклоны и определяют валентность элемента. Полную, действительную валентность элемент обретёт тогда, когда подобную группу удастся разбить, т.е. затратить известную энергию. Изложенное, как видим, по сути не так далеко от нынешних представлений.

Борис Гуляев (Растутаев)

Февраль 1986 г., февраль 1990 г.

г. Вологда