Кинетика и механизм инактивации электронотранспортной цепи изолированных хлоропластов

Как отмечалось выше, экспоненциальный закон надежности широко распространен при отказе различного рода систем. Возможно, этот закон применим для описания процессов инактивации сложных биологических структур. При этом нужно учитывать динамический характер биоструктур, их изменчивость, способность к трансформации в формы, отличные по свойствам от исходных.

Кинетическая модель, основанная на экспоненциальном характере отказов биологических органелл, рассмотрена в работах [466, 501, 502]. Эта модель была разработана для описания процесса инактивации электронотранспортной цепи хлоропластов и объяснения эффекта активации электронного транспорта в процессе "старения". При "старении" в сложной организации органелл могут иметь место последовательные изменения, приводящие к образованию по структуре отличных частиц, которые сохраняют в той или иной степени функциональную активность. Структурные изменения могут приводить к образованию большого набора форм (Х₁, Х₂ ... Х_n), различающихся функциональной активностью. Активность каждого типа частиц может быть как выше, так и ниже активности исходной формы. Структурные изменения, приводящие к изменению свойств органелл, протекают во времени, и каждый такой переход можно охарактеризовать своей константой скорости (k₁, ... k_n-1). Модифицированные формы, образовавшиеся в результате структурных изменений, могут обладать не только различной активностью, но и различной устойчивостью к денатурационным воздействиям. В предположении, что каждый сорт частиц инактивируется независимо по экспоненциальному закону, интенсивности отказов каждой формы можно охарактеризовать своей величиной λ₁, ... λ_n.

Функциональная активность каждой формы, которая определяется по каталитической активности в какой-либо функционально важной реакции, пропорциональна концентрации этой формы. Коэффициенты пропорциональности заданы в виде α₁, ... а_n. Определяемая на опыте общая активность является аддитивной функцией активности каждого сорта частиц. Кинетическая схема, которая соответствует описанному выше механизму "старения" электронотранспортной цепи, имеет вид

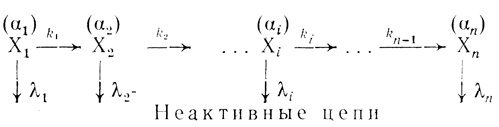(3.94)

Здесь X₁ ... Х_n - структурно и каталитически различающиеся формы электронотранспортной цепи; k₁, ... k_n-1 - константы скорости структурных изменений в процессе "старения"; λ₁, ... λ_n - интенсивности отказов каждой из форм.

В соответствии с законами химической кинетики изменение концентраций в процессе "старения" каждой из форм описывает система из взаимосвязанных дифференциальных уравнений.

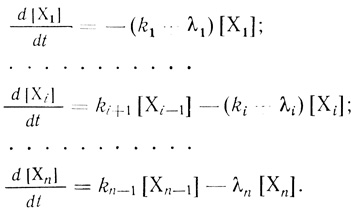(3.95)

Определяемая на опыте общая активность дается уравнением

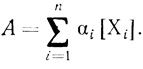(3.96)

Таким образом, задача кинетического описания процесса инактивации электронотранспортной цепи в процессе "старения" в рамках рассматриваемой модели сводится к решению системы линейных дифференциальных уравнений с постоянными коэффициентами (3.95). Решение такого рода систем уравнений применительно к задачам химической и ферментативной кинетики детально рассмотрено в [466, 254]. Характеристическое уравнение системы в форме определителя можно представить в виде

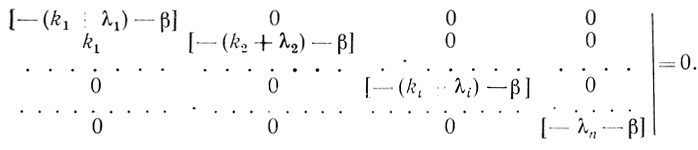(3.97)

Решение этого диагонального определителя дает уравнение

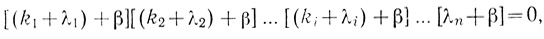(3.98)

которое позволяет найти все n действительных однократных β_i корней:

Таким образом, определяемая на опыте активность суспензии хлоропластов в соответствии с уравнениями (3.96) и (3.99) дается функцией

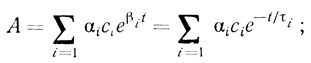(3.100)

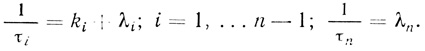(3.101)

Проведенный анализ позволяет сделать два важных вывода:

1. Кинетическая кривая изменения активности в процессе "старения" электронотранспортной цепи, каждая форма которой характеризуется постоянной во времени интенсивностью отказов, описывается суммой экспоненциальных членов, причем число экспонент соответствует числу форм цепи, различающихся по активности или стабильности. Таким образом, если наблюдаемая на опыте кинетическая кривая описывается суммой n экспоненциальных членов, это говорит о том, что в механизме "старения" принимает участие как минимум n форм электронотранспортной цепи. Очевидно, что структурных различий, накапливаемых в процессе "старения", учитывая сложность системы, может быть бесконечно много, однако из кинетических данных по инактивации можно получить информацию лишь о тех формах, которые отличаются от исходных либо активностью, либо стабильностью, либо тем и другим.

2. Несмотря на кажущуюся сложность процесса "старения", анализ показывает, что кинетика процесса отражает набор некоторых "элементарных" стадий. Для схемы (3.94), в которой все процессы необратимы, можно получить кинетические характеристики отдельных "элементарных" стадий. Получаемые характеристические времена связаны с константами скорости процессов структурных изменений и частотами отказов отдельных форм простым соотношением (3.101). Каждое обратное характеристическое время представляет собой сумму константы скорости превращения данной формы и интенсивности ее инактивации. При построении кинетической схемы (3.94) предполагалось, что процессы, приводящие к изменению свойств электронотранспортной цепи, необратимы. Можно показать, что кинетическое описание системы существенно не изменится, если допустить, что некоторые стадии в процессе трансформации цепи обратимы. В этом случае соотношения, связывающие константы скорости и интенсивности отказов с характеристическими временами, будут существенно сложнее, однако природа кинетической зависимости будет той же.

Проведенный анализ такой сложной с физико-химической точки зрения системы, как электронотранспортная цепь хлоропластов, позволяет говорить об "элементарных" стадиях процесса инактивации. Весьма осторожно следует говорить об элементарных константах скорости процессов, поскольку даже в простейшем случае (схема 3.94) наблюдаемые характеристические времена являются функциями элементарных констант скорости и интенсивности отказов. Важно подчеркнуть, что кинетический механизм "старения", представленный схемой (3.94), в достаточной степени идеализирован. Тем не менее этот механизм представляется весьма общим. Основным предположением, заложенным в построение этой кинетической модели, является экспоненциальный характер отказов отдельных форм органелл в процессе их структурных изменений. Как отмечалось выше, постоянность интенсивности отказов есть частный случай более общей зависимости. Тем не менее этот случай весьма широко распространен в природе.

Рассмотренная кинетическая модель была использована для экспериментального анализа процесса "старения" электронотранспортной цепи изолированных хлоропластов [466, 501, 502]. Суспензию изолированных хлоропластов инкубировали при постоянной температуре, брали пробы и исследовали способность хлоропластов проводить реакцию фоторазложения воды и фотовосстановления феррицианида калия. Типичный вид наблюдаемых зависимостей активности суспензии от времени представлен на рис. 43 и 50. В процессе инкубации и "старения" хлоропластов их активность в реакции фотовосстановления феррицианида калия возрастает, проходит через максимум и падает до нуля. Анализ показывает, что кинетика инактивации описывается суммой по крайней мере двух экспоненциальных членов.

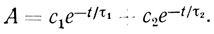(3.102)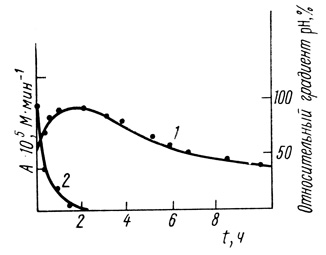

Рис. 50. Сравнение кинетики инактивации хлоропластов (1) и кинетики уменьшения трансмембранного градиента pH (2)

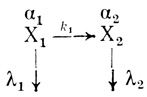
В рамках рассмотренной кинетической модели зависимость активности хлоропластов от времени типа (3.102) означает, что в механизме инактивации принимает участие как минимум две формы электронотранспортной цепи хлоропластов, различающиеся по активности и интенсивности отказов:

(3.103)

Схема (3.103) удовлетворительно описывает наблюдаемые экспериментальные данные. Анализ этой схемы приводит к следующему уравнению зависимости активности суспензии хлоропластов от времени инкубации, при условии, что в начальный момент времени все электронотранспортные цепи хлоропластов находились в форме Х₁.

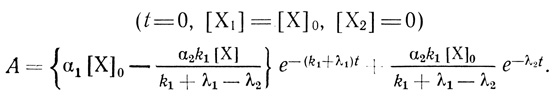(3.104)

В соответствии с этим уравнением из данных, приведенных на рис. 43, следует, что τ₁ = 1,42 Ч, τ₂ = 3,3 Ч, соответственно k₁ + λ₁ = 0,7 ч^-1, λ₂ = 0,4 ч^-1.

Уравнение (3.104) при α₂ > α₁ описывает феномен увеличения активности хлоропластов в процессе "старения".

Для экспериментальных данных, представленных на рис. 43, параметры А₀, С, τ₁ и τ₂ соответственно равны 8,8⋅10^-6 м/мин, 4⋅10^-5 м/мин; 1,42 ч и 3,3 ч. Среднее время безотказной работы системы в соответствии с уравнением (3.69) равно 10,1 ч. Увеличение активности хлоропластов в процессе старения существенно повышает эффективное среднее время работы.