Математические модели молекул

С тех пор как химия встала, по выражению Ф. Энгельса, "с головы на ноги", т. е. на научную основу, она так или иначе стала обращаться к математике как к наиболее универсальному языку для выражения своих законов, понятий и представлений. Особенно широкое применение математических методов в химии стало возможным после создания статистической термодинамики, феноменологической кинетики и т. п. Однако со второй половины прошлого века некоторые математики обращаются к химии, пытаясь найти корреляции между математическими структурами и теориями химии, в частности теорией химического строения. К сожалению, эта линия в истории химии, а точнее, в истории связей между химией и математикой, до сих пор оказывалась вне поля зрения историков науки. Поэтому необходимо остановиться на ней отдельно, тем более, что исследования, проводимые на стыке математики и химии в прошлом столетии, повлияли на развитие теории спин-валентности.

В XIX в. в естествознании стали складываться такие ситуации, когда сначала разрабатывался математический аппарат, а уже потом начинались поиски или "случайно" находились его вне* математические интерпретации. Клейн писал в "Эрлангенской программе": "... не следует умалять значение того преимущества, которое дает хорошо выработанный формальный аппарат для дальнейших исследований тем, что он до известной степени опережает мысль..." [15, с. 428].

Хронологически первой математической работой в области структурной химии была работа английского математика Артура Кэли [32], который пытался решить задачу о подсчете числа изомеров парафинов с заданным числом атомов углерода. При этом валентность атома выступала как степень вершины графа (точнее, дерева), который математически представлял химическое соединение, а именно: единица - для атома водорода и четыре - для атома углерода. Заметим, что значение валентности отнюдь не выводилось из каких-либо математических соображений, а постулировалось (вводилось в теорию) на основании химических данных. Спустя четыре года появились работы английских математиков Сильвестра [81] и Клиффорда [34], посвященные подмеченной ими формальной аналогии между соотношениями и понятиями теории химического строения и начавшей тогда развиваться алгебраической теории инвариантов. Мы не будем останавливаться подробно на этих исследованиях, а ограничимся только теми аспектами, которые оказались "математическими предвестниками" теории спин-валентности.

Каждому атому X, Y, ... в рамках указанной формальной аналогии сопоставлялся некоторый двумерный вектор, например:

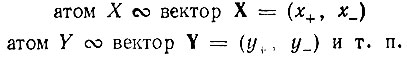
Тогда можно образовать некоторую алгебраическую форму F(X, Y,...), в которую векторы X, Y,... входят в соответствующих целых неотрицательных степенях V_X, V_Y ,..., причем V_I сопоставляется с валентностью 1-го атома. Эта форма остается инвариантной относительно унитарного преобразования компонент (х₊, х_-), (у₊, у_-) и т. п.^*

^* (Разные математики, разрабатывавшие эту аналогию, использовали различные формы ее выражения. Наше изложение ближе к тому, которое дал Вейль [7], хотя во многих местах и отличается от него.)

Для двух векторов (двух атомов) X и Y простейшим инвариантом будет следующее выражение: которому формально сопоставлялась единичная химическая связь и которое первоначально называли одночленным инвариантом. Одночленным инвариантам давалась следующая графическая интерпретация: если X и Y обозначить точками на плоскости, то [XY] представляет собой отрезок, соединяющий эти точки.

Далее, математически можно ввести также некоторый "свободный" вектор L. Не вдаваясь в подробности, касающиеся математических свойств L, можно указать, что графически одночленному инварианту, составленному из L и одного из "обычных" векторов," например X, соответствует направленный отрезок, начало которого лежит в точке X, а конец остается свободным X → L. Выражение [XL] можно интерпретировать как свободную валентность атома X.

Если между атомами X и Y существует несколько химических связей, например k, то математически этому случаю соответствует выражение [XY]^k. Аналогично целое неотрицательное число f в выражении [XL]^f указывает на число свободных валентностей атома X.

Произведению инвариантов, не содержащих свободного вектора, можно сопоставить некоторую классическую структурную формулу. Однако не все произведения одночленных инвариантов, составленные для совокупности атомов с заданными валентностями, будут независимы. Поясним сказанное примером молекулы бензола, в которой каждый из атомов углерода образует по одной связи с двумя соседними атомами углерода и ближайшим атомом водорода. Так как, согласно классической теории, углерод четырехвалентен, то необходимо рассмотреть возможные сочетания оставшихся нереализованными шести единиц валентности по одной от каждого углеродного атома.

Можно составить довольно много всевозможных произведений одночленных инвариантов:

но только пять из них являются линейно независимыми (например, I, V, VI, VII и VIII). Оставшиеся инварианты можно представить в виде линейной комбинации этих пяти, в частности:

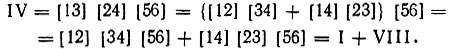
Выбранным линейно независимым инвариантам соответствуют структуры, изображенные на рис. 3. Первые две из них называются структурами Кекуле, остальные три - структурами Дьюара.

Исследования "химико-алгебраической аналогии", начатые Сильвестром и Клиффордом, были затем продолжены в работах по теории инвариантов В. Г. Алексеева [1, 45]. Различаясь по способу математической интерпретации постулатов теории химического строения, эти работы оказались сходными в трактовках понятий валентности и химической связи, которые обладали следующими особенностями: а) валентность того или иного элемента определялась из химических, а не из математических соображений; б) валентность явно или неявно выступала как сумма кратностей связей, образуемых данным атомом с другими, причем единичной химической связи между атомами X и Y соответствовал одночленный инвариант [XY].

Указанная аналогия была скептически встречена некоторыми математиками (Нетер, Штуди). Штуди, например, писал, что "было бы слишком фантастическим ожидать, будто химия когда-либо извлечет пользу из этой ветви алгебры". Однако появлением квантовой механики положение изменилось. Если в XIX - начале XX вв. речь шла, по словам Вейля, "о исто формальной, хотя и очень впечатляющей математической аналогии", то в конце 20-х годов говорится уже о "существеннейшем звене в квантовомеханической теории химической связи, которой указанная аналогия имеет ... удивительно конкретное воплощение" (Вейль).

Выше мы рассмотрели основные направления теоретических исследований, которые подготовили почву для перехода от классической теории химического строения к квантовомеханической. Итак, можно выделить два подготовительных этапа создания квантовой теории химической связи. Первый, формально-математический, включает работы 1870 г.- 1900-х гг. (Кэли, Сильвестр, Клиффорд, Гордан, В. Г. Алексеев), в которых были предприняты попытки построения математических моделей молекул, основанные на теории инвариантов бинарных форм и теории химического строения. Второй подготовительный этап, электронный (1900-1926 гг.), включает работы, посвященные созданию электронных (как статических, так и динамических) моделей атомов и молекул.

При этом на обоих подготовительных этапах каждой ковалентной связи (валентному штриху) сопоставлялись некоторые дискретные объекты: либо это были компоненты двумерных векторов в формально-математических моделях, либо - отдельные электроны, занимающие определенные положения в атомах и молекулах (статические модели) или же двигающиеся по определенным траекториям (динамические модели). Как в математических, так и в физико-химических работах содержались рациональные идеи, вошедшие после соответствующей кванто-вомеханической интерпретации в квантовую химию: идея двухцентровой двухэлектронной связи (Льюис), возможность обобществления нескольких электронов вокруг двух и большего числа ядер (Ленгмюр), идея неподеленной электронной пары (Льюис, Сиджвик), разделение электронных и ядерных движений (Вор, Ван Флек, Зоммерфельд и др.), идея одноэлектронного приближения (Бор), сопоставление ковалентной связи некоторого математического выражения [XY], антисимметричного относительно перестановки своих компонент (Сильвестр, Алексеев и др.) и т. п.

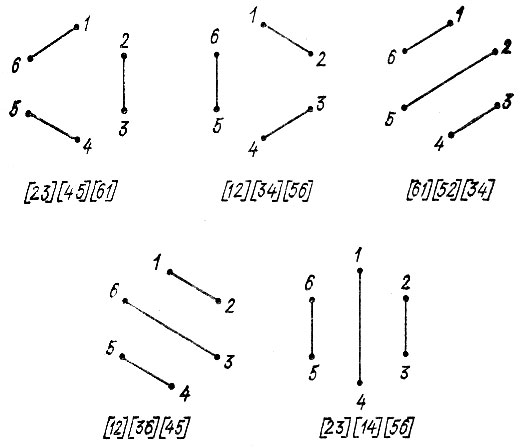
Рис. 3. Линейно-независимые инварианты и соответствующие им структуры бензола

Создание в 1925-1926 гг. квантовой механики позволило глубоко проникнуть в сущность явлений и процессов, протекающих в атомах и молекулах, выявить физический смысл понятия химической связи и других понятий классической химии.

В конце 20-х годов были установлены общие квантовомеханические принципы и приближения, необходимые для описания многоэлектронных систем. Как и в период разработки электронных моделей (1900-1926 гг.) строения вещества, каждая квантовомеханическая модель химической связи существенно опиралась на квантовомеханическую (шредингеровскую) модель атома. На протяжении всей последующей эволюции теории многоэлектронных систем указанная взаимосвязь между теорией атома и теорией молекул сохранялась. Поэтому прежде чем приступить к рассмотрению основных этапов развития молекулярной квантовой химии и некоторых ее современных проблем, в следующей главе мы остановимся на основных понятиях и представлениях квантовой теории строения атома.