Молекула и ее движения

Молекулу иногда еще определяют как наименьшую частицу вещества, сохраняющую его химические свойства. По крайней мере, вторая часть этого определения неверна. Если свойства вещества действительно зависят от строения и свойств отдельных молекул, то отдельная молекула какого-то вещества - это .еще не вещество, а микрочастица и не может обладать его свойствами. Всем ясно, что о таких характерных физических свойствах веществ, как температуры кипения и плавления, упругость пара, твердость, вязкость и т. д., говорить применительно к одной молекуле бессмысленно. Но не всегда все понимают, что и химические свойства вещества и свойства одной молекулы - это не одно и то же. Способность веществ вступать в химические, реакции зависит не только от строения и свойств их молекул, но и от концентраций, температуры, давления паров, вероятностных (энтропийных) факторов и т. д. Еще сложнее зависимость скоростей протекания тех или иных химических реакций, Следует иметь также в виду, что очень многие чистые в обычном химическом понимании вещества бывают образованы молекулами одного и того же состава, но несколько различного строения в силу наличия динамической или подвижной изомерии. Иными словами можно сказать, что во многих веществах молекулярного состава (об атомарных газах, металлах, ионных кристаллах и т. п. мы в этой книжке говорить вообще не будем) возможно существование различных форм молекул, непрерывно взаимопревращающихся друг в друга, т. е. находящихся в динамическом равновесии, положение которого зависит от внешних условий. С одним из видов такой подвижной изомерии мы будем иметь дело в этой книге.

Молекулу можно определить как образованную химически связанными атомами электронейтральную микрочастицу определенного состава и строения. Молекулы заданного состава и строения, исключая различия в строении динамических изомеров, в совокупности образуют молекулярное вещество с определенными характерными для него физическими и химическими свойствами. В общем случае мы не делаем различий между молекулами органических, неорганических и комплексных соединений. Кроме того, очень многое, что будет говориться ниже о молекуле, относится и к другим химическим частицам - таким, как молекулярный ион, отличающийся наличием некомпенсированного положительного или отрицательного электрического заряда, или свободный радикал, отличающийся наличием у него ненасыщенной валентности, и т. д.

Как же, вкратце, развивались представления о строении молекул и в чем сущность наших современных представлений?

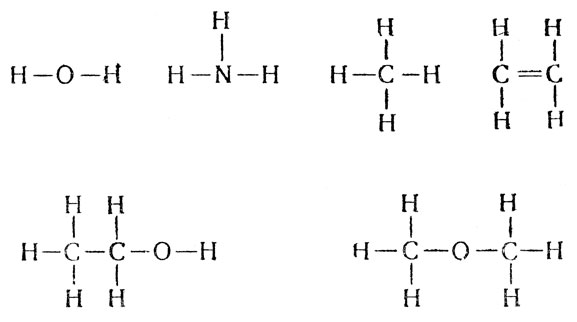
К пониманию атомно-молекулярной структуры вещества химия пришла еще на очень раннем этапе своего развития, а соответствующие этому научные представления были четко сформулированы уже в первой половине XVIII века нашим великим соотечественником М. В. Ломоносовым. Однако основы фундаментального учения о строении молекул или теории химического строения были заложены значительно позднее. До середины XIX века химики могли говорить только о составе вещества, т. е. о том, из какого числа атомов и атомов каких элементов образована молекула данного химического соединения, что отражалось соответствующей, как ее называют, брутто формулой: Н₂О - вода, NH₃ - аммиак, СН₄ - метан, С₂Н₄ - этилен, С₂Н₆О - этиловый спирт и диметиловый эфир и т. д.

В 1861 году А. М. Бутлеров впервые ввел понятие химической структуры и разработал положение о порядке химической связи атомов в молекуле. Это нашло свое отражение в языке структурных формул, например для тех же молекул: Такими формулами, показывающими последовательность и кратность (черточки символизируют число валентностей) химических связей атомов, пользуются и до настоящего времени, хотя они и не могут выразить всех особенностей строения молекул. Большой вклад в создание классической теории химического строения, наиболее четко и последовательно сформулированной Бутлеровым, внесли также Франкланд, Кекуле, Купер и др. В дальнейшем, продолжая ее развитие, Вант-Гофф и Лебель заложили основы классической стереохимии, но только в последнее время пришедшие на помощь химикам физические методы исследования позволили определять геометрию молекулы и сделали пространственные представления неотъемлемой частью учения о строении молекул.

Открытие электрона и проникновение в тайны строения атома, физическая интерпретация периодического закона Д. И. Менделеева и другие достижения экспериментальной и теоретической физики позволили уже в нашем веке на базе квантовой механики и современных физических и физико-химических методов исследования вскрыть новые факты и закономерности в строении молекул, понять природу химической связи атомов, заново пересмотреть некоторые основные понятия и представления теории химического строения. "Само собой разумеется, - говорил А. М. Бутлеров^*,- что когда мы будем знать ближе натуру химической энергии, самый род атомного движения, - когда законы механики получат и здесь приложение, тогда учение о химическом строении падает, как падали прежние химические теории, но подобно большинству этих теорий, оно падет не для того, чтобы исчезнуть, а для того, чтобы войти в измененном виде в круг новых и более широких воззрений".

^* ( А. М. Бутлеров. Чтение в Общем собрании физико-химического общества, 1879 г. - В сб. Столетие теории химического строения. М., Изд-во АН СССР, 1961, стр. 127.)

Главными в учении о строении молекул и сейчас остаются проблемы теории химической связи. Когда два атома, соединяясь в молекуле, образуют химическую связь, то по крайней мере часть их электронов, так называемых внешних или валентных, обобществляется. Эти отрицательные элементарные частицы перестают принадлежать лишь одному атому, а движутся теперь в поле обоих положительно заряженных атомных ядер, так что где-то между ними возникает участок или участки наибольшей электронной плотности. Сгустки электронной плотности как бы удерживают около себя или стягивают эффективные^* ядра атомов, что и соответствует возникновению химической связи. По мере развития таких представлений валентным штрихам структурных формул классической теории химического строения стали придавать смысл локализованных двухцентровых двухэлектронных связей, образуемых парами электронов с антипараллельными магнитными моментами (спинами). Однако накопленный материал показал недостаточность такого описания химических связей. Законы квантовой механики требуют рассматривать все электроны молекулы (по крайней мере внешние электроны всех атомов) в поле всех ядер, образующих скелет молекулы. Если даже видеть смысл валентного штриха структурной формулы в том, что он указывает на электронную плотность, в среднем соответствующую двум электронам, то и в этом случае есть много примеров полной неприменимости классических формул строения (соединения переходных металлов с ненасыщенными органическими молекулами, ферроцен и Др.). Пример молекулярного иона водорода, Н₂+, уже наглядно показывает, что химическая связь может осуществляться и одним электроном. Когда структурные формулы в указанном выше смысле применимы, они все-таки недостаточны, так как не отражают, например, пространственного строения молекулы и. некоторых других особенностей.

^* (Под эффективным ядром мы понимаем остов, включающий собственно положительное ядро и необобществленные внутренние электроны атома.)

Незыблемым в понятии строения молекулы является то, что в силу большой массы ядер по сравнению с электронами (на 3 порядка) они могут быть легче локализованы в молекуле, т. е. легче можно определить их относительное расположение. Этим объясняется и жизнеспособность бутлеровских формул строения, отражающих порядок расположения атомов в цепи химического действия в молекуле, и возможность определения с помощью современных физических методов пространственной геометрической конфигурации ядерного скелета молекулы. Определенному пространственному расположению ядер отвечает единственно возможное при этом распределение электронной плотности, хотя мы далеко не всегда можем отчетливо себе его представить.

Таким образом, одной из важнейших основ наших знаний о строении молекул является знание равновесных (см. ниже) геометрических конфигураций их ядерных скелетов, которые можно изображать, соединяя ядра по химическим связям черточками, независимо от того, сколько электронов в среднем приходится на каждую химическую связь. Бутлеровские формулы строения и пространственные модели ядерных скелетов молекул хотя и недостаточны, но необходимы для понимания химического строения молекул и будут, по-видимому, еще долго и широко использоваться.

Молекула представляет динамическую систему, образованную ядрами и электронами, которые находятся в непрерывном движении. Рассмотрим, какие же основные виды движений характерны для этой микрочастицы и, соответственно, из каких основных составляющих складывается ее энергия. Возьмем сначала в качестве примера простейший случай двухатомной молекулы, причем неважно, будет ли это молекула водорода (Н₂), хлористого водорода (НС1), азота (N₂) или любая другая молекула, образованная двумя атомами одного или разных элементов. Будем говорить об "изолированной" молекуле, т. е. не испытывающей сильных межмолекулярных взаимодействий и влияния внешних полей, и отвлечемся от поступательного движения молекулы в пространстве, которое практически не сказывается на ее внутреннем строении. При этом тремя основными составляющими полной энергии молекулы будут: энергия электронного движения в поле ядер, Е_эл, энергия колебательного движения ядер относительно положений равновесия, Е_кол, и энергия вращения молекулы как целого, Е_вр, т. е. Е_мол=Е_эл+Е_кол+Е_вр

У всякой молекулы возможны только вполне определенные состояния всех этих видов движений и только вполне определенные квантованные значения составляющих энергии, которая, следовательно, может меняться не непрерывно, а дискретно (скачкообразно).

Начнем с наиболее важного вида движения и наибольшей составляющей энергии. Обобщенные электроны атомов в молекуле, образующие химическую связь, определенным образом распределены и движутся в поле эффективных ядер, удерживая их в едином комплексе на каком-то расстоянии друг, от друга. Характер распределения электронной плотности, т. е. состояние движения электронов в молекуле, может меняться с соответствующим скачкообразным изменением электронной составляющей энергии молекулы. Существуют, таким образом, различные электронные состояния или уровни энергии. Электронное состояние с наименьшей возможной энергией является основным, наиболее устойчивым, тогда как другие состояния - возбужденными, менее устойчивыми. Сообщая энергию, можно возбудить молекулу, т. е. заставить ее перейти на более высокий электронный уровень, Е'_эл .С другой стороны, если возбужденная молекула переходит в более низкое энергетическое состояние, E"_эл, то она отдает энергию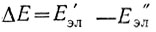

Когда энергообмен происходит с электромагнитным излучением, оказывается, что кванты поглощаемой или отдаваемой энергии при переходах молекул из одного электронного состояния в другое соответствуют по частоте, 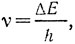, ультрафиолетовой, видимой и иногда самой близкой инфракрасной областям электромагнитного спектра. В этих областях и наблюдаются так называемые электронные спектры испускания или поглощения молекул, позволяющие исследовать различные электронные состояния молекул и определять важнейшие энергетические и другие характеристики последних в этих состояниях.

В любом электронном состоянии молекулы, пока существует достаточно устойчивая химическая связь между атомами, положительные ядра также не остаются в покое, а совершают непрерывное колебательное движение относительно положений равновесия. Двухатомную молекулу можно представить как систему связанных точечных масс m₁ и m₂ (размеры ядра пренебрежимо малы по сравнению с размерами атома и молекулы):

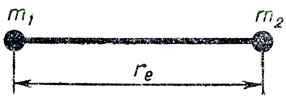
В результате ее колебательного движения непрерывно меняется единственный геометрический параметр - межатомное или межъядерное расстояние, r. Равновесным положениям ядер соответствует некоторое среднее равновесное межатомное расстояние, r_e, которое и принимается за геометрическую характеристику двухатомной молекулы. Кривая зависимости потенциальной энергии, v, молекулы от межатомного расстояния, r, показана на рис. 1. Минимум кривой соответствует равновесному расстоянию между ядрами; при сильном сближении ядер потенциальная энергия в силу их отталкивания быстро растет, а при сильном растяжении молекулы - сначала растет из-за противодействия силам связи, а затем приходит к постоянному значению, соответствующему системе из невзаимодействующих атомов после диссоциации молекулы, т. е. разрыва химической связи.

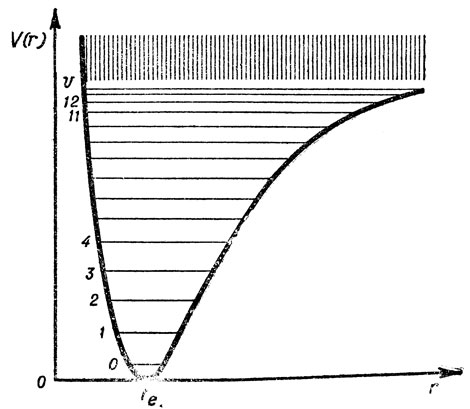
Рис. 1. Потенциальная кривая двухатомной молекулы, совершающей негармонические колебания

У молекулы возможны вполне определенные колебательные состояния или колебательные уровни энергии. В приближении гармонических колебаний квантовая механика дает следующее выражение колебательной энергии: 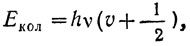, где v - колебательное квантовое число, которое может принимать значения 0, 1, 2, 3, 4 и т. д., a v соответствует классической частоте колебаний и связана с характеристиками молекулы соотношением 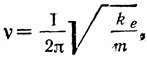здесь m - приведенная масса 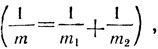, a k_e- силовая постоянная, характеризующая упругие свойства связи. Легко заметить, что колебательная энергия никогда не равна нулю,так как даже при v = 0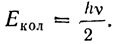

Переходы молекул (в заданном электронном состоянии) из одного колебательного состояния в другое соответствуют меньшим изменениям энергии, чем электронные переходы, и могут сопровождаться испусканием или поглощением электромагнитного излучения в инфракрасной области спектра. Колебательные частоты могут быть экспериментально определены не только методом инфракрасной спектроскопии, но и другими методами (например, методом комбинационного рассеяния света), на которых мы не можем здесь останавливаться. Колебательные спектры несут большую информацию о строении молекул, с которой мы еще отчасти встретимся ниже.

Вращение молекулы как целого в пространстве также подчиняется не классическим, а квантовомеханическим законам и может происходить лишь с определенными значениями угловой скорости и частоты. Иными словами, существуют определенные вращательные состояния или вращательные уровни энергии. В приближении жесткой двухатомной молекулы квантовая механика дает для них следующее выражение: 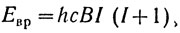, где I - вращательное квантовое число, принимающее значения 0, 1, 2, 3, 4 и т. д., а В - вращательная постоянная (здесь в единицах см^-1), обратно пропорциональная моменту инерции (I = mr²_e ) молекулы.

Находясь в каком-то электронном и колебательном состояниях, молекула может менять вращательное состояние, причем переходы между вращательными уровнями энергии сопровождаются выделением или поглощением очень небольших квантов энергии, которые по частоте соответствуют далекой инфракрасной области электромагнитного спектра или области микрорадиоволн. Изучая вращательные спектры молекул методами инфракрасной или микроволновой спектроскопии, а также спектроскопии комбинационного рассеяния света, можно получить значения моментов инерции, геометрические параметры молекул и другие ценные данные об их строении.

Итак, для двухатомной молекулы можно представить показанную на рис. 2 качественную диаграмму относительного расположения электронных, колебательных и вращательных энергетических уровней (взяты только два электронных состояния), Очевидно, что когда в заданном электронном состоянии меняется колебательное состояние молекулы, то при этом неизбежно меняется и вращательное состояние: каждому колебательному уровню соответствует свой набор вращательных подуровней энергии. Когда же меняется электронное состояние, то одновременно меняются и колебательное, и вращательное состояния. Отсюда можно понять сложную структуру молекулярных спектров, наблюдаемых в ультрафиолетовой, видимой и инфракрасной областях. В массе вещества при заданных внешних условиях существует определенное распределение молекул по их энергетическим состояниям, и свойства вещества зависят не только от строения и свойств молекул, но и от статистического распределения их по энергетическим уровням.

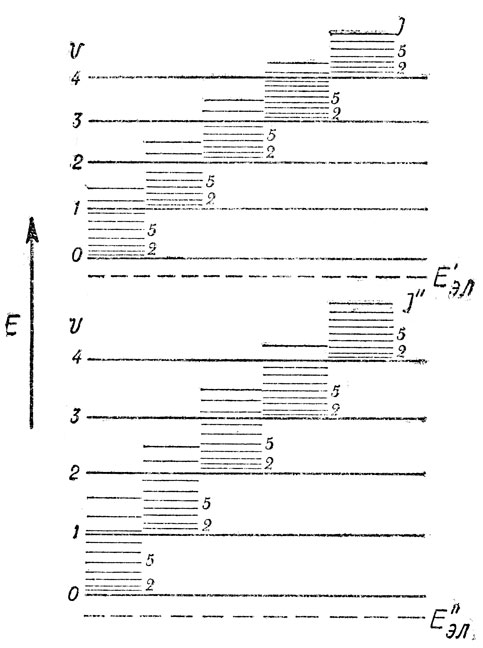
Рис. 2. Схема относительного расположения энергетических уровней двухатомной молекулы

В случае любой многоатомной молекулы можно представить в сущности аналогичную картину, которая, естественно, будет значительно сложнее: кроме того, при рассмотрении таких молекул возникают и многие дополнительные вопросы. Не говоря уже о сложности распределения электронной плотности в многоатомных молекулах и картины возможных электронных состояний, в них очень сильно возрастает число колебательных степеней свободы и, соответственно, основных колебательных уровней энергии. Действительно, если молекула состоит из N атомов, то для описания относительного расположения ядер в пространстве требуется не один, как у двухатомной молекулы, а в общем случае 3N-6 (для линейных молекул 3N-5) геометрических параметров или обобщенных координат^*.

^* ( Положение N точечных масс в пространстве описывается 3N координатами (например, в декартовой системе). Если же эти точечные массы связаны между собой, то для описания поступательного движения всей такой системы (ее центра тяжести) без изменения относительного расположения точечных масс в системе достаточно 3 координат. Для описания вращательного движения системы без изменения относительного расположения точек также нужны 3 (для линейной системы 2) координаты (углы Эйлера). Таким образом, остается только 3N-6 (3N-5) координат для описания расположения точек друг относительно друга.)

Ядра, как и в двухатомной молекуле, не остаются в покое, а колеблются относительно своих равновесных положений, при этом все 3N-6 (3N-5) геометрических параметров могут сложным образом меняться. Таким образом, у многоатомной молекулы имеется соответствующее число колебательных, степеней свободы и столько же основных колебательных уровней энергии. За каждым основным следуют возбужденные энергетические состояния, в том числе и составные (совместные) для нескольких основных.

Вращение пространственной молекулы, как и любого объемного тела, может рассматриваться относительно трех взаимно перпендикулярных главных осей, характеризуется тремя главными моментами инерции, но подчиняется, как и в случае двухатомной молекулы, законам квантовой механики. Расположение вращательных уровней энергии зависит от общей формы И симметрии молекулы. Естественно, что свободное вращение и вращательные переходы молекул в общем случае возможны только в газообразном состоянии веществ.

В химии принято и для многих случаев вполне оправданно - пользоваться средними энергетическими характеристиками молекул (внутренними энергиями, энергиями связей атомов и т. д.). Дело в том, что термохимическими методами, например, могут быть определены теплоты или энергии образования только определенных количеств вещества, скажем, граммоля. Внутренняя энергия такого количества вещества, отнесенная к одной молекуле (поделенная на число Авогадро - число молекул в граммоле), и будет средней энергетической характеристикой данной молекулы. При этом сказанное выше о статистическом распределении отдельных молекул по энергетическим состояниям остается в силе.

Имея в виду изложенное выше о движении молекулы, необходимо условиться, что подразумевать под пространственной геометрической конфигурацией молекулы, в частности ее ядерного скелета. Во-первых, обычно молекула рассматривается в основном, невозбужденном, электронном состоянии. При изменении электронного состояния геометрические параметры молекулы могут существенно изменяться, и если говорится о ее геометрии в каком-то возбужденном электронном состоянии, то это обязательно должно быть указано. Во-вторых, обычно пренебрегают вращением молекулы как целого, хотя оно может незначительно влиять на ее геометрию. В специальных работах это влияние может являться предметом рассмотрения. Наконец, в-третьих, считают, что молекула находится в низких по энергии колебательных состояниях, и берут некоторые средние для них равновесные значения геометрических параметров. Эти условия и определяют так называемую равновесную ядерную конфигурацию молекулы.

Очень важной характеристикой геометрической конфигурации молекулы является ее симметрия. Симметрия вообще подразумевает наличие у того или иного объекта некоторых элементов симметрии; им соответствуют определенные операции симметрии, выполнение которых оставляет объект без каких бы то ни было изменений. Существуют следующие элементы и операции симметрии^*.

^* ( Мы рассматриваем не все из них, а только такие, которые оставляют в покое по крайней мере одну точку пространства.).

1. Ось симметрии порядка n, обозначаемая С_n; соответствующая операция симметрии - поворот вокруг оси на угол (360°/n)р, где р - целочисленный множитель, меняющийся от 1 до n-1. Порядок оси n может быть равным 2, 3, 4, 5, 6 и т. д. Так, например, через центр равностороннего треугольника перпендикулярно его плоскости проходит ось симметрии третьего порядка, С₃, а соответствующие ей операции симметрии суть повороты вокруг оси на углы 120 и 240°. Для общности вводится также представление об оси "симметрии" первого порядка, С₁, или элементе тождественного преобразования, I, которым соответствует операция "поворота" на 0° ;(объект в покое). Такой элемент есть у любого объекта.
2. Плоскость симметрии, σ; соответствующая операция симметрии - отражение в плоскости, при котором каждая точка объекта, лежащая с одной стороны на плоскости, находит себе подобную на таком же кратчайшем расстоянии по другую сторону плоскости. Так, правильный цилиндр имеет, бесчисленное количество плоскостей симметрии, пересекающихся на оси цилиндра бесконечного порядка (С_∞). Каждая из этих плоскостей рассекает цилиндр вдоль на две равные половины. Кроме того, у правильного цилиндра есть одна плоскость симметрии, секущая его поперек (на две равные половины), которая перпендикулярна оси С_∞ ,
3. Центр симметрии, i; соответствующая операция - инверсия или отражение в центре симметрии, представляющем особую точку. Суть этой операции состоит в том, что для любой точки объекта после проведения от нее прямой через центр симметрии можно найти на таком же расстоянии от центра совершенно подобную точку. Центром симметрии является, например, центр шара, центр куба и т. д.
4. Зеркально-поворотная ось порядка n, S_n; соответствующая операция симметрии включает, поворот вокруг оси на угол (360°/n)р (относительно значений р см. выше; n может быть n лишь четным) и последующее отражение в плоскости, перпендикулярной оси. Иллюстрировать этот элемент и эту операцию симметрии на общеизвестных предметах несколько труднее.

Ниже мы встретимся с зеркально-поворотными осями и другими элементами симметрии на примерах некоторых молекул.

Объект может иметь не обязательно один, но и сразу несколько элементов симметрии. Однако возможны лишь вполне определенные сочетания элементов или операций симметрии. Возможные совокупности рассмотренных операций симметрии образуют так называемые точечные группы симметрии. Самыми простейшими группами являются С₁, C_t (S₂), С₂ и C_s, когда нет ни одного или имеется только по одному элементу симметрии в "совокупности" (соответственно: нет элементов, центр симметрии, который тождествен S2, ось второго порядка и плоскость). Примерами простых точечных групп, включающих несколько элементов и операций симметрии, являются С_2h и C_2v Первая из них включает ось симметрии С₂, перпендикулярную ей плоскость симметрии и центр симметрии, находящийся на пересечении оси и плоскости. Вторая - имеет ось симметрии С₂ и две взаимно перпендикулярные плоскости симметрии, пересекающиеся на этой оси.

Чем выше порядок осей симметрии и чем больше элементе; симметрии образуют какую-либо совокупность, тем выше считается симметрия точечной группы, При исключении редко встречающейся оси С₅ и всех осей симметрии порядка выше 6 можно, например, показать, как это сделали в восьмидесятых годах прошлого века выдающийся русский кристаллограф Е. С. Федоров и немецкий математик А. Шёнфлис, что существует всего лишь 32 точечных группы симметрии. Любую молекулу можно отнести по симметрии ее ядерного скелета к одной из возможных точечных групп.

Многие свойства молекул уже полностью определяются ее равновесной ядерной конфигурацией. Симметрия ядерного скелета, например, определяет симметрию всей молекулы, т.е. и распределения электронной плотности. Электрические свойства молекул: дипольный момент, 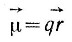, q - заряд, 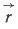- расстояние между "центрами тяжести" отрицательных и положительных зарядов) и поляризуемость, α (способность электронов и ядер смещаться под действием внешнего электрического поля), также зависят от геометрии равновесной ядерной конфигурации. Так, например, полярность или неполярность вещества, т. е. неравенство или равенство нулю дипольного момента молекулы данного вещества, полностью определяется симметрией равновесной ядерной конфигурации. Если у молекулы есть центр симметрии или пересекающиеся друг, с другом оси симметрии, то обязательно μ= 0. С геометрической конфигурацией молекулы и ее симметрией тесно связаны энергетические, оптические и другие свойства вещества, например частотные характеристики и интенсивности спектров.

Естественно, что мы не могли бы справиться здесь с задачей даже краткого рассмотрения всех вопросов строения и свойств молекул. Вопрос о пространственном строении и видах изомерии молекул, которого касается эта книжка, представляет в настоящее время один из основных вопросов в теории химического строения. В частности, все современные квантовомеханические расчеты в любом приближении проводятся и, видимо, долго еще будут возможны лишь на моделях с фиксированными в пространстве ядрами.