§ 1. Параметры решетки и число формульных единиц в ячейке

Параметры элементарной ячейки а, b, с входят непосредственно в условия Лауэ, их легко определить по положению дифракционных рефлексов на рентгенограммах.

Наиболее простой метод решения задачи состоит в оценке параметра по слоевым линиям рентгенограммы вращения (см. гл. II, § 8). Положение слоевых линий на рентгенограмме определяет растворы дифракционных конусов, коаксиальных оси вращения кристалла, а следовательно (через соответствующее условие Лауэ),

и период повторяемости в узловых рядах, параллельных оси вращения. Если с осью вращения совмещена ось X кристалла, то по расстоянию между p-той и экваториальной слоевой линией l_p и радиусу кассеты R (см. рис. 33, а) можно определить угол раствора конуса: l_p/R=ctgφ(р). Отсюда, используя условие Лауэ, находим параметр а:

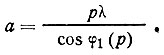
Из трех рентгенограмм вращения (или вращательного качания) определяются все три линейных параметра решетки: а, b и с.

Точность определения этим методом периодов повторяемости невысока. Но его преимущество заключается в том, что для нахождения параметров не требуется знания всех трех индексов каждого рефлекса.

С другой стороны, даже грубая оценка параметров решетки существенно облегчает индицирование рентгенограмм (в особенности рентгенгониометрических снимков) или установку кристалла и счетчика дифрактометра в отражающее положение для разных отражений pqr. Затем можно уточнить параметры решетки, используя координаты (в случае дифрактометра - установочные углы) наиболее "дальних" рефлексов дифракционных лучей с высокими индексами pqr.

По геометрии размещения рефлексов на рентгенограммах можно оценить и угловые параметры решетки. Последнее существенно только при исследовании моноклинных и триклинных кристаллов.

Зная параметры решетки, нетрудно найти объем элементарной ячейки кристалла V₀, а следовательно, и число формульных единиц соединения, приходящихся на ячейку. Это число определяется как отношение массы элементарной ячейки V_0p (где р - плотность) к массе одной формульной единицы Mg (где М - молекулярная масса; g=1,66*10^-22 г - масса атома водорода). Поскольку плотность вещества измеряется в г/см³, а объем ячейки в А³ и так как 1 А³=10^-24 см³, окончательное уравнение имеет вид

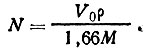(22)

Экспериментально определяемая плотность (например, пикнометрическим или флотационным методом) относится к реальному кристаллу, имеющему трещины и другие дефекты. Обычно она несколько ниже плотности идеального кристалла, и поэтому формула (22), как правило, дает несколько заниженный (не целочисленный) результат.

Подставляя затем вместо N целое число, по формуле (22) можно оценить p_рент - плотность идеального монокристалла. Эта величина является важным параметром для ряда технических применений кристаллов, например для оценки эффективности энергоемких систем.