Суперпозиционный метод

В принципе распределение межатомной функции можно использовать для значительно более глубокого анализа атомного расположения. И хотя восстановление общей картины р(r) по Р(u) в общем случае представляет собой довольно сложную задачу, ряд практических приемов такого восстановления ("деконволюции" паттерсоновского распределения) уже разработан.

Общую основу этих приемов можно установить, если несколько видоизменить процедуру построения паттерсоновского распределения по распределению электронной плотности. Вернемся к модели элементарной ячейки с точечными атомами (см. рис. 42) и соответственно к паттерсоновскому пространству с дискретными точками- максимумами. Переход от первой ко второму нагляднее всего представить как перенос жесткого контура, связывающего все атомы ячейки (рис. 45, а), в паттерсоновское пространство при последовательном совмещении с началом координат каждого из атомов структуры. Поместив в начало координат, например, вершину 1 контура (т. е. атом 1), найдем положение всех максимумов, расположенных в концах векторов r₁₂, r₁₃, r₁₄, ... (рис. 45, б). В соответствии с формулой (48) мощности этих максимумов должны составить р₁p₂, p₁p₃, p₁p₄,... Это означает, что их следует взять пропорциональными электронным плотностям соответствующих атомов (2, 3, 4, ...) с коэффициентом пропорциональности, равным плотности первого атома р₁. Поместив таким же образом в начало координат вершину 2 контура, получим максимумы 21, 23, 24, ... Им следует приписать мощность, пропорциональную соответственно р₁ р₃, р₄,... при коэффициенте пропорциональности р₂. Последовательным перемещением в начало координат всех вершин контура можно получить все максимумы паттерсоновского пространства. Иначе говоря, паттерсоновское распределение можно представить как суперпозицию всех возможных смещений структуры с коэффициентами пропорциональности, равными плотности в точке, помещенной в начало координат^*.

^* (Как видно из выражения (45), эта формулировка сохраняет силу и при переходе к непрерывному распределению электронной плотности.)

Спрашивается, можно ли решить обратную задачу: восстановить по суперпозиционной картине модель самой структуры? Оказывается, можно. Общее доказательство этого положения потребовало бы довольно много места^*.

^* (Порай-Кошиц М. А. Практический курс рентгеноструктурного анализа. М., Изд-во МГУ, 1960. Т. II. С. 481 и сл. )

Гораздо проще показать на модельном примере, как эта задача решается. Изготовим три копии рис. 42, б, т. е. три копии паттерсоновского пространства с точечными максимумами, и вложим их друг в друга так, чтобы все максимумы совпали. Это будет исходным положением (рис. 46, а) (максимумы копии I изображены кружками; копии II- вертикальными штрихами; копии III - горизонтальными штрихами). Сместим теперь начало координат второй и третьей копий в один из максимумов первой копии, например, в пик А, как показано на рис. 46, б (вектор перемещений r_A). Часть максимумов копий II и III снова наложилась на пики копии I. Рассмотрим только наложенные максимумы. Нетрудно видеть, что они содержат в себе контур искомой структуры плюс его инверсированное изображение (точка инверсии находится в середине вектора перемещения Гл). Сместим теперь начало координат последней третьей копии в один из выделенных уже максимумов, например в пик В. Результат показан на рис. 46, в. Оставшиеся вложенными друг в друга пики всех трех копий воспроизводят исходный контур без каких-либо добавлений или пропусков.

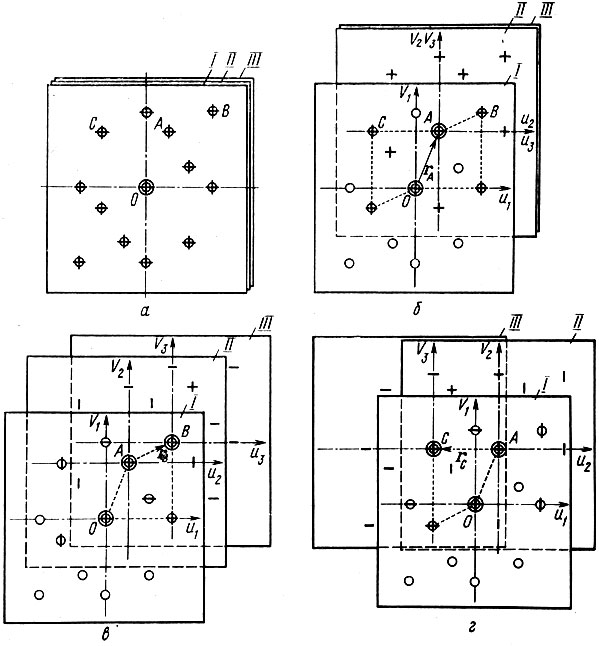
Рис. 46. Общий метод выделения структуры из паттерсоновской функции: а - три копии паттерсоновской функции, вложенные друг в друга с совпадением начал их координат; б - смещение копий II и III в максимум А; в - смещение копии III в максимум В; г - смещение копии III в максимум С

Заметим, что если бы последнее смещение копии III было выполнено не в точку В, а, скажем, в точку С, то тройное наложение выделило бы не исходную, а инверсированную структуру (рис. 46, г). Но так или иначе задача восстановления структурной модели была бы решена независимо от того, какой из пиков, выделенных при первом смещении, взять за основу для второго смещения копий.

Описанная схема выделения структурного контура лежит в основе так называемых суперпозиционных методов решения структурной задачи.

До сих пор рассматривалась модель структуры, построенной из точечных атомов. Реально же приходится иметь дело с электронной плотностью, распределенной непрерывно по элементарной ячейке и соответственно с функцией Р(u), непрерывной в паттерсоновском пространстве. Необходимо, следовательно, найти такой оператор, который был бы адекватен той процедуре, которая была проведена при наложении трех копий Р(u) со сдвигом, а именно, уничтожению всех не совпавших максимумов и сохранению всех совпавших по положению. Такая математическая функция, в точности отвечающая переходу от Р(u) к р(r) при суперпозиции, пока еще не найдена. Одна из лучших приближенных операций, отвечающих такому переходу, заключается в минимизации плотности Р(u). Это понятие предполагает сохранение в каждой точке пространства наименьшего из трех наложенных значений межатомной функции:

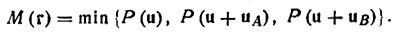(49)

Если В данной точке любая из трех паттерсоновских копий имеет малое (фоновое) значение, то в М(r)-функции сохранится лишь эта фоновая величина. Но если все три копии в данной точке дают повышенное значение межатомной функции (подъемы к максимумам), то сохранится наименьшее из всех, но тоже повышенное значение. При совпадении трех пиков сохранится наименьший по высоте максимум. В результате распределения М(r) окажется грубым воспроизведением распределения электронной плотности по ячейке^*:

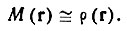(50)

Полученное "минимизованное" распределение М(r) можно подвергнуть визуальному кристаллохимическому анализу - постараться выявить в нем черты структуры, удовлетворяющие обычным кристаллохимическим требованиям, опираясь на число атомов в элементарной ячейке, их относительные и абсолютные веса, допустимые межатомные расстояния и т. п. Такой анализ может выполнять и вычислительная машина.

^* (Более строгое доказательство соотношения (50) можно найти в кн.: Порай-Кошиц М. А. Практический курс рентгеноструктурного анализа. М., Изд-во МГУ, 1960. Т. II. С. 488.)

Однако автоматизация процесса решения структурной задачи может быть проведена и иначе. Коль скоро М(r) приближенно передает распределение р(r), можно использовать интегральную формулу (33), подставив в нее М(r) вместо р(r), и рассчитать знаки (или начальные фазы) всех отражений^*, начав тем самым кругооборот между формулами (35) и (28).

^* (Симонов В. И., Щедрин Б. М. - Кристаллография. 1961. 6. № 3, 363.)