
Глава 2. Электрон в поле постоянного потенциала
В качестве примера решения уравнения Шредингера рассмотрим задачу об электроне, заключенном в прямоугольную потенциальную яму с шириной а и бесконечной глубиной (рис. 2.1.). Хотя для этого случая вычисления очень просты, результаты их иллюстрируют некоторые важные свойства квантовомеханических систем: квантование энергии, наличие квантовых чисел и так называемой нулевой энергии. Эта задача о частице в потенциальном ящике является основой приближения свободных электронов в методе молекулярных орбиталей, которое обсуждается в гл. 15.
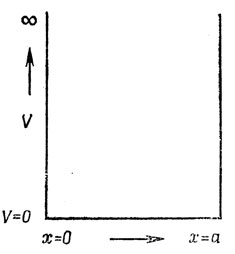
Рис. 2.1. Прямоугольная потенциальная яма
Решение одномерного уравнения Шредингера (1.11)
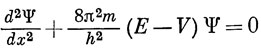
в области постоянного потенциала имеет вид
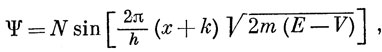
где k и N - постоянные интегрирования. В этом можно убедиться, подставляя выражение (2.2) в уравнение (2.1).
Внутри потенциальной ямы V = 0, так что
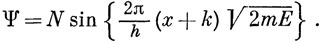
Если V = ∞, то для конечных значений энергии функция У должна равняться нулю [см. уравнение (2.1)]. Следовательно, решения (2.3) допустимы только в том случае (поскольку они должны быть однозначны), если Ψ = 0 при х = 0 и х = а*). Таким образом, функция W должна иметь вид
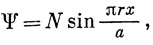
где r = 1, 2, 3, ... (2.4)
*) (Если V - конечно, и Ψ и Е должны быть конечны, то
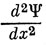
также должна быть конечна.
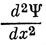
только в том случае конечна, если Ψ и dΨ/dx - непрерывные функции аргумента х. Но если V = ∞, то уравнение (2.1) может иметь решение с бесконечной
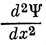
Таким образом, в точке, где потенциал обращается в бесконечность, непрерывность
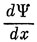
не обязательна.)
Сравнивая уравнения (2.3) и (2.4), замечаем, что k = 0 и
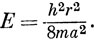
Далее, видно что наложение граничных условий приводит к квантованию энергии: разрешены только состояния с энергией, удовлетворяющей соотношению (2.5). Здесь r - квантовое число, которым можно нумеровать состояния электрона и уровни энергии: Ψr и Еr. Заметим, что состояние Ψ0 не существует (функция Ψ0 во всех точках обращается в нуль). Самое нижнее состояние Ψ1 имеет энергию, которую называют нулевой энергией. Поскольку V = 0, вся эта энергия является кинетической. Другими словами, даже в самом нижнем по энергии состоянии электрон движется, как это и должно быть, если не нарушается принцип неопределенности Гейзенберга. Ψr2 есть плотность вероятности нахождения электронов в точке, принадлежащей интервалу изменения x от 0 до а. Поскольку полная вероятность, получаемая интегрированием, равна 1, условие нормировки (1.14) в рассматриваемом случае имеет вид
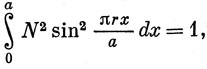
что дает
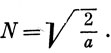
Рис. 2.2. иллюстрирует решения задачи. Функции Ψr похожи на амплитуды основного (Ψ1) и обертонов (Ψ2, Ψ3, ...) колебаний натянутой струны.
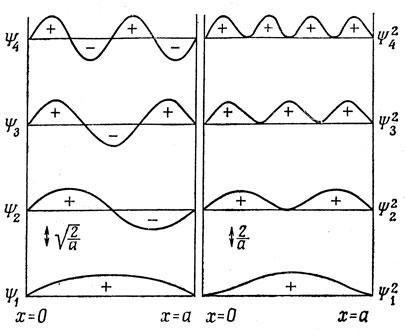
Рис. 2.2. Волновые функции и плотности вероятности для первых четырех решений задачи об электроне в потенциальном ящике
Обратимся теперь к двумерному потенциальному ящику (рис. 2.3) и будем решать уравнение
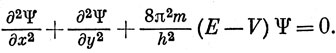
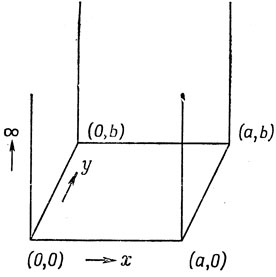
Рис. 2.3. Двумерная потенциальная яма
Если потенциал V можно представить в виде суммы функций, одна из которых зависит только от x, а другая - только от y, то волновая функция Ψ может быть изображена как произведение функций, одна из которых зависит только от x, а другая - только от y. В этом случае говорят, что переменные в дифференциальном уравнении разделяются. В частности, при V = 0 решение уравнения (2.8) есть произведение решений двух одномерных уравнений (2.3):
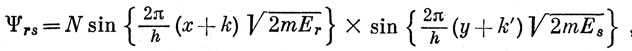
причем Е = Er + Es, а k, k' и N - постоянные.
Налагая, как и в одномерном случае, граничные условия, находим, что квантовые числа r и s - целые и
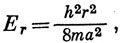
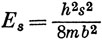
N = 2 / √ab.
В основном состоянии
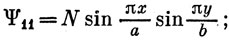
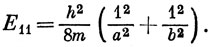
Для следующих, энергетически более высоких состояний
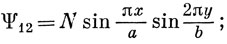
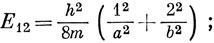
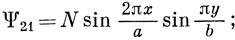
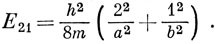
Для квадратного потенциального ящика (а = b) Ψ21 и Ψ12 соответствуют одной и той же энергии. В таком случае говорят, что имеется вырождение. В общем количество квантовых чисел равно числу измерений ящика, и это справедливо, даже если ящик не прямоугольный. Как будет видно, уровни энергии электронов в атоме (трехмерная задача при наличии сферической симметрии) характеризуются тремя квантовыми числами.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'