
1. Лимитирующие стадии
В последние годы проведено большое число количественных исследований скоростей реакций с участием ферментов. В настоящее время на основе этого материала можно сделать некоторые выводы об общих свойствах ферментативного катализа как природного феномена. Ферментативный катализ как всякое природное явление имеет определенные ограничения в параметрах молекулярных процессов, поэтому представляет интерес оценка средних характеристик ферментативных реакций и границ эффективности ферментов.
Зависимость начальной стационарной скорости для большинства изученных ферментативных процессов имеет "классический" вид, заданный уравнением Михаэлиса-Ментен:
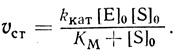 (2.1)
(2.1)Эта зависимость отражает участие в механизмах ферментативных превращений лабильных промежуточных соединений фермента с субстратом [252].
Константа скорости kкат, входящая в уравнение 2.1, характеризует лимитирующую, самую медленную стадию процесса. Чтобы доказать это положение, рассмотрим стационарную кинетику процесса с участием произвольного числа n промежуточных соединений [253, 254].
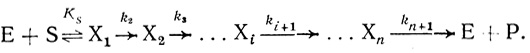 (2.2)
(2.2)Для простоты предполагается, что первая стадия реакции имеет обратимый характер, последующие стадии практически необратимы. В стационарном состоянии по промежуточным соединениям (d[Xi]/dt = 0) кинетику процесса описывает система уравнений
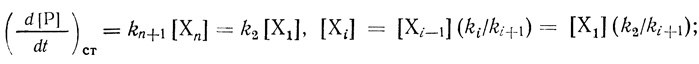 (2.3)
(2.3)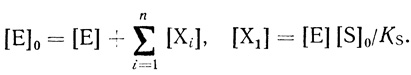
Начальная стационарная скорость реакции имеет вид
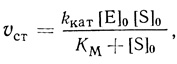 (2.4)
(2.4)где
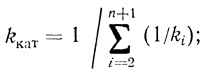 (2.5)
(2.5)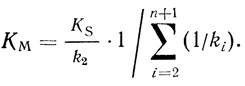 (2.6)
(2.6)Параметр kкат часто называют "числом оборотов" фермента, поскольку он равен числу актов превращения субстрата одним активным центром фермента в единицу времени.
Скорость процесса в стационарном состоянии определяет медленная, лимитирующая стадия процесса. Действительно, если какая-либо "элементарная" стадия цепи превращений субстрата в конечный продукт самая медленная и характеризуется наименьшей константой kj скорости
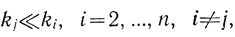 (2.7)
(2.7)то уравнения (2.5), (2.6) приобретают вид
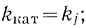 (2.8)
(2.8)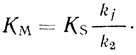 (2.9)
(2.9)Если константы скорости двух процессов имеют соизмеримые характеристики (ki ∼ kj), кинетические параметры ферментативной реакции можно представить в виде
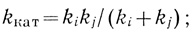 (2.10)
(2.10)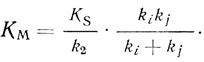 (2.11)
(2.11)Важно отметить, что для реакций, протекающих в соответствии с кинетической схемой (2.2), величина kкат/KМ имеет ясный физический смысл и представляет собой эффективную бимолекулярную константу скорости k2/KS образования из фермента и субстрата промежуточного соединения Х2 (или продуктов реакции, если реакция двухстадийная).
Обычно в серии химически родственных субстратов лимитирующей является одна и та же стадия. Например, в катализе α-химотрипсином гидролиза сложноэфирных субстратов - производных аминокислот - практически для всех изученных субстратов лимитирующей является стадия гидролиза промежуточного ацилфермента (k3), в гидролизе всех амидов и анилидов - его образование [255, 256].
Таким образом, значение kкат представляют собой наиболее важные характеристики ферментативных реакций, отражающие самый медленный процесс в активном центре фермента.
Интересно проанализировать численные значения каталитических констант скорости и констант Михаэлиса различных ферментов с тем, чтобы представить эффективность ферментативного катализа в целом. В настоящее время в литературе имеется большой материал по величинам υмакс, КМ и соответственно при известной концентрации фермента по величинам kкат [253, 254, 257-259]. В монографии [10] впервые сделана попытка статистического анализа констант скоростей лимитирующих стадий ферментативных реакций.
Нами проведен общий статистический анализ кинетических констант kкат, констант Михаэлиса и параметров kкат/KМ [260, 261]. Всего проанализировано около 80 ферментов, выбранных статистически независимо. В анализе использованы данные монографий и обзоров [10, 253, 256-259], а также журналов "Biochim. Biophys. Acta", "J. Biol. Chem.", "Biochemistry", 1971-1976. Для ферментов, кинетические параметры которых определены по различным субстратам, использовано значение для наиболее "быстрого" (по kкат или kкат/KМ) субстрата в оптимальных условиях процесса.
В первом приближении не обнаруживается закономерного распределения ферментов по эффективности в соответствии с катализируемой реакцией. Один и тот же класс ферментов может включать как "быстрые", так и сравнительно медленные ферменты.
Нами были найдены функции плотностей распределения ферментов. С этой целью ферменты были разбиты на группы с приблизительно одинаковыми константами процесса (в пределах одного порядка), определялось число ферментов в группе, полученные значения нормировались к общему числу ферментов в выборке. На рис. 10, 11, 12 приведены кривые плотности распределения ферментов по величинам kкат, КМ и kкат/КМ.
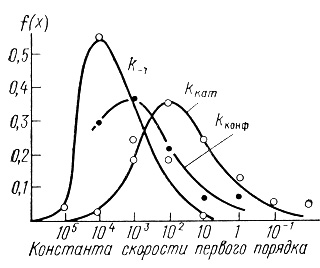
Рис. 10. Плотности распределения констант скоростей в ферментативном катализе (константы скорости первого порядка)
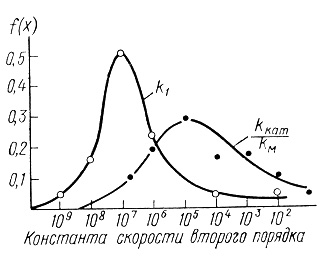
Рис. 11. Плотности распределения констант скоростей в ферментативном катализе (константы скорости второго порядка)
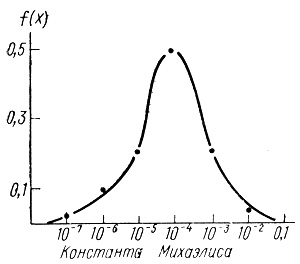
Рис. 12. Плотности распределения констант Михаэлиса в ферментативном катализе
Кривые, приведенные на этих рисунках, отражают вероятность того, что случайно выбранный фермент будет обладать заданным параметром kкат, КМ или kкат/КМ. Кроме того, путем интегрирования плотности распределения может быть вычислена вероятность того, что выбранный наугад фермент обладает кинетическими характеристиками в заданном диапазоне.
Полученные плотности распределения достаточно близки к нормальной кривой Гаусса. Кривые kкат, kкат/КМ на рис. 10, 11 и кривая рис. 12 имеют теоретический характер и вычислены по уравнению
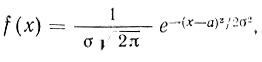 (2.12)
(2.12)где x = lgkкат; lgKM или lgkкат/КМ соответственно.
Параметры кривых приведены в табл. 14 [260].

Таблица 14
* (Данное значение kкат/КМ отличается от величины, которую можно было бы получить из данных рис. 10 и 12. Это связано с тем, что при построении рис. 11 для некоторых ферментов использовались параметры kкат/KМ субстратов, имеющих большее значение этого параметра.)
По своей каталитической эффективности ферменты могут различаться более чем в 106 раз. Распределение ферментов по kкат в общем представляется достаточно узким. Среднеквадратичное отклонение составляет величину одного порядка. При этом практически отсутствуют ферменты, имеющие kкат = 106 с-1 и выше. Наиболее широко распространены ферменты, лимитирующие стадии реакций с которыми имеет порядок 102 с. Удивительно, что в отличие от обычных химических реакций, масштаб изменения констант скоростей которых практически безграничен, ферменты весьма унифицированы по кинетическим параметрам. "Типичный" фермент имеет kкат ∼ 100 с-1 и KМ ∼ 10-4 М.
Существующий энергетический барьер 10-17 ккал/моль на лимитирующих стадиях процесса обусловлен, по-видимому, рядом физико-химических эффектов. Из анализа функции плотности распределения ферментов по величинам kкат (см. рис. 10) можно сделать интересный вывод, связанный с функционированием полиферментных систем. Обычно биохимическая трансформация веществ протекает многостадийно с последовательным участием большого набора ферментов. Можно ожидать, и это является наиболее вероятным, что полиферментная цепь будет лимитироваться ферментом с каталитической константой около 102 с-1.
Величина константы Михаэлиса характеризует эффективность комплексообразования субстрата активным центром фермента, а также в ряде случаев относительную кинетическую устойчивость промежуточных соединений. Фактический диапазон изменения этого параметра от 10-2 до 10-7 М. Наиболее часто встречаются ферменты, имеющие Км около 10-4 М. Важно отметить, что в выборке отсутствуют ферменты, у которых КМ меньше 10-7 М. Таким образом, поскольку KS ≥ KM, предельная "эффективность комплексообразования" фермента с субстратом характеризуется величиной свободной энергии около 10 ккал/моль. Почему в ферментативном катализе отсутствуют более прочные "комплексы Михаэлиса"? Ответ на этот вопрос не достаточно ясен. Однако можно думать, что ферменты избегают образования чрезвычайно устойчивых "комплексов", существование которых определило бы наличие глубоких энергетических впадин на пути превращения субстрата в продукт реакции.
Параметр kкат/КМ для различных ферментов варьируется в диапазоне 101-1010 M-1⋅c-1 [11]. Наиболее распространены ферменты с kкат/KМ около 105 М-1⋅с-1. Пределом значений kкат/KМ является величина 1010 М-1⋅с-1. Как показано в работе [263], значение kкат/КМ характеризует нижний предел констант скоростей биомолекулярных стадий в ферментативном катализе. Известно, что для реакций в растворе предельные скорости биомолекулярных реакций определяются молекулярной диффузией реагентов и характеризуются величиной 1010 М-1⋅с-1 [264-266].
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'