Сопоставление математической модели с экспериментальными данными

Для расчета параметров модели из экспериментальных данных была выбрана серия экспериментов для мембраны толщиной 0,8 см. Оценка левой части неравенства (2.94) с использованием значения Км нативного фермента показала, что большая часть экспериментальных точек, полученных на мембранах толщиной 0,8 см, удовлетворяет этому неравенству. Поэтому расчет параметров модели проводился на основе приближения ступенчатого фронта реакции.

Очевидно, что в рамках ступенчатой модели можно определить только три параметра, входящих в уравнения этой модели (2.93) и (2.69); υ_макс; К_М^* = К_М/Р₂ и D^* = aP₁D₁.

Алгоритм численного решения обратной задачи был следующий. Пусть имеется n экспериментальных значений потоков j_эксп(i), где i = 1, 2, ..., n, соответствующих различным начальным концентрациям [S₁]₀(i) и [S₂]₀(i) и заданным значениям l = 0,8 см и А = 10 см². Для каждого i по формуле (2.92) вычисляется функция ξ^*(i), для которой аргументами являются υ_макс, К_М^* и D^*. Затем в зависимости от выполнения неравенств ξ^* ≤ 1 или ξ^* ≥ 1 по формулам (2.93) или (2.69) для каждого набора аргументов υ_макс, К_М^* и D^* определяются значения потоков j(i). Решение обратной задачи сводится к минимизации функции. Вычисления проводил на машине БЭСМ-6 А. А. Бельнов.

Найденные значения параметров, отвечающие минимальному значению критерия качества Q = 0,909, равны: υ_макс = 2,4⋅10^-6 г⋅эквН/л⋅с; К_М/Р₂ = 1,2⋅10^-5 М; aP₁D₁ = 5⋅10^-7 см²⋅г⋅экв/с⋅моль. В табл. 22 сравниваются экспериментальные потоки водорода и рассчитанные с использованием полученных значений параметров. Согласие результатов можно считать удовлетворительным - с учетом того, что в каждом отдельном опыте может несколько варьироваться процент сохраняющего активность иммобилизованного фермента, а также могут в некоторой степени различаться свойства самого геля. В табл. 22 приведены также рассчитанные для каждого случая значения ξ координаты границы двух зон. Видно, что дитионит натрия лишь тогда проникает через всю пластину, когда его концентрация более чем на четыре порядка превышает концентрацию метилвиологена.

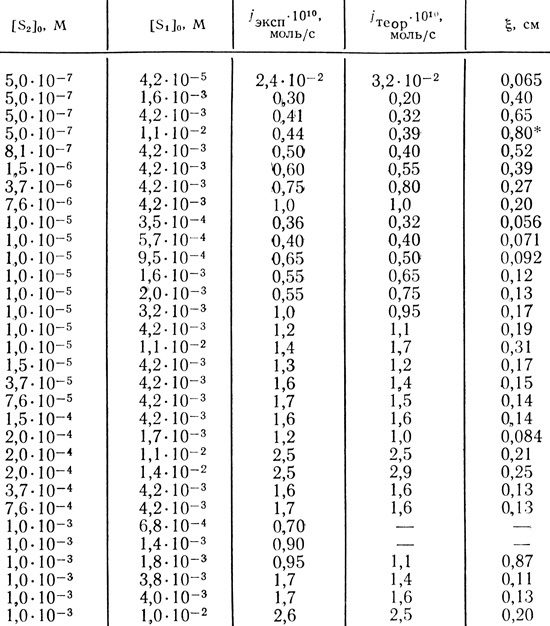
Таблица 22. Экспериментальные и теоретические величины потоков водорода и координаты границы зон для мембран 0,8 см

^* (Дитионит натрия проникает через всю мембрану.)

Как следует из данного выше анализа, кинетические характеристики действия иммобилизованной гидрогеназы и диффузионной подвижности субстрата получены в результате достаточно сложных вычислений, позволивших учесть эффекты диффузионного массопереноса субстратов реакции. Была необходима независимая проверка модели. С этой целью из двух независимых экспериментов были определены параметры υ_макс, K_М/P₂ и эффективный коэффициент диффузии aP₁D₁.

а) Измерение скорости реакции на тонких пластинках. Из табл. 22 видно, что основная часть экспериментальных данных на пластинках толщиной 0,8 см получена в условиях, далеких от насыщения, при ξ^* << 1 (хотя для одновременного определения υ_макс и aP₁D₁ в этой серии опытов достигалось также и полное насыщение). Серия кинетических измерений проведена на более тонких пластинках толщиной 0,18 см в условиях, когда дитионит натрия проникал через всю толщину пластины ([S₁])₀ ≥ 10^-2 М). Эту серию можно рассматривать как независимое определение υ_макс и К_М/Р₂ в чисто кинетической области. Для тонких мембран, которые равномерно насыщены дитионитом натрия, концентрация восстановленной формы метилвиологена постоянна по всему объему и процесс протекает в кинетическом режиме. Рассчитанные из зависимости скорости от концентрации субстрата параметры оказались равными υ_макс = (3,2±0,6)⋅10^-6 г⋅экв Н₂/л⋅с и K_М/P₂ = (1±0,2)⋅10^-5 М, что удовлетворительно согласуется с результатами экспериментов на толстых пластинах, включающих эффекты диффузионного массопереноса.

б) Измерение перемещения границы окрашенной зоны реакции. Прямое определение коэффициента распределения и коэффициента диффузии в геле дитионита натрия - вещества, крайне легко окисляемого кислородом воздуха, представляет собой сложную экспериментальную задачу. Для независимого определения параметра aP₁D₁ была применена специальная методика, которая заключается в визуальном наблюдении за перемещением фронта первой стадии реакции (2.59) при диффузии дитионита натрия в столбике акриламидного геля, предварительно насыщенного окисленной формой метилвиологена S₂'. Движение фронта регистрировали по распространению синей окраски, присущей восстановленной форме метилвиологена S₂ (форма бесцветна). По существу постановка эксперимента отличалась от основных кинетических опытов только тем, что в акриламидный гель не вводили фермент, т. е. в системе отсутствовала вторая стадия реакции (2.59).

Соответствующая нестационарная диффузионная задача решена в работе [348]. Положение границы между зонами двух вступающих в реакцию веществ S₁ и S₂' подчиняется уравнению

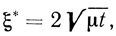(2.96)

где t - время; μ - постоянная, являющаяся корнем трансцендентного уравнения

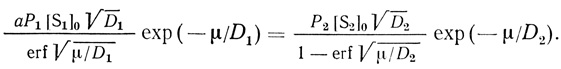(2.97)

Постоянная μ легко определяется экспериментально.

Преобразуем (2.97) следующим образом:

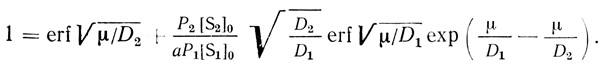(2.98)

При условии N₃ << 1 и не сильно различающихся значениях D₁ и D₂ из уравнения (2.97) следует, что еrf√(μ/D_i) ≈ 1, где i = 1, 2.

Приведем функцию erf√(μ/D₂) в правой части (2.97) к виду:

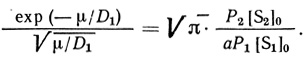(2.99)

Это уравнение соответствует приближению ступенчатого изменения концентраций S₂' и S₂. Чтобы найти с помощью (2.99) одновременно D₁ и aP₁/P₂, достаточно определить μ, хотя бы для двух различных отношений концентраций:

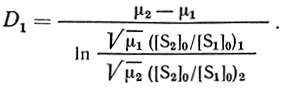(2.100)

Экспериментальные данные приведены на рис. 23. Наличие отчетливо наблюдаемой, резко выраженной движущейся границы - само по себе прямое подтверждение предложенной выше модели ступенчатого фронта реакции.

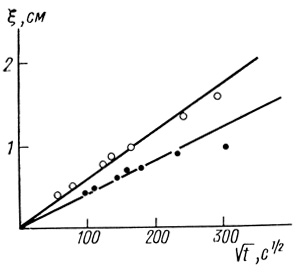
Рис. 23. Исследование границы окрашенной зоны в нестационарном режиме

По данной методике получены следующие значения параметров: D₁ = (1,5±0,8)⋅10^-6 см²/с; aP₁/P₂ = 0,4±0,2 г⋅экв/моль. Из специальных равновесных опытов была оценена величина коэффициента распределения метилвиологена Р₂ = 2,0±1,0. Отсюда aP₁D₁ = (1,2±0,9)⋅10^-6 см²⋅г⋅экв/с⋅моль.

В таблице 23 приведены кинетические и диффузионные параметры системы, полученные из данных различного характера. Видно, что в пределах ошибки эксперимента параметры, найденные на основании предложенной математической модели, согласуются с параметрами, полученными из двух независимых экспериментов.

Таблица 23

^* (Из данных по кинетике движения окрашенной зоны найдено (1,2±0,9)⋅10^-6 см²⋅г⋅экв/моль⋅с.)

На основе изложенной выше кинетической модели, подтвержденной экспериментом, можно решить обратную задачу - расчет потоков водорода в зависимости от условий проведения процесса, концентраций компонентов, толщины мембраны (см. табл. 22). Важным представляется теоретический расчет профилей концентраций компонентов реакции. Соответствующие кривые, полученные расчетным путем на основании параметров, данных в табл. 22, приведены на рис. 24.

Рис. 24. Профили концентраций дитионита натрия в системе дитионит натрия-метилвиологен-гидрогеназа для пластины 0,8 см. Концентрации субстратов: 1 - [S₁]₀ = 5,7⋅10^-4 М, [S₂]₀ = 1,0⋅10^-6 М; 2 - [S₁]₀ = 3,2⋅10^-3 М, [S₂]₀ = 10^-5 М; 3 - [S₁]₀ = 4,2⋅10^-3 М, [S₂]₀ = 5⋅10^-7 М; 4 - [S₁]₀ = 4,2⋅10^-3 М, [S₂] = 1,5⋅10^-4 М

Таким образом, проведенный анализ действия иммобилизованной гидрогеназы привел к разработке детальной кинетической модели действия фермента, позволяющей в конечном итоге количественно рассчитать работу полученного гетерогенного катализатора на основе знания кинетических параметров действия фермента и диффузионных характеристик компонентов реакции.