
Клетка как мембранный микрореактор
Большой интерес представляет проблема исследования кинетики и механизма действия ферментов в нативном состоянии в клетках. Непосредственное определение кинетических параметров ферментов в клетках в рамках общих задач биологической кинетики является важным шагом в понимании механизма действия ферментов и регуляторных особенностей клеточных реакций. С другой стороны, биокаталитические процессы с использованием клеток, в частности, процессы микробиологического характера, составляют существенную часть современной биотехнологии. Конверсия сложных молекул углеводного характера в газообразное топливо (водород или метан) с высокими КПД и скоростями протекает в клетках различных микроорганизмов. Исследование количественных закономерностей ферментативных реакций в этих условиях представляется достаточно важным.
В настоящей работе в соответствии с общей программой изучения физико-химических проблем биоконверсии энергии с получением и использованием водорода проведено исследование кинетических закономерностей действия гидрогеназ, продуцирующих молекулярный водород в клетках бактерий.
В общем случае кинетику химических превращений с участием клеток невозможно рассматривать в отрыве от транспортных эффектов, связанных с массопереносом веществ через внешнюю цитоплазматическую мембрану. Для многих веществ основной барьер, который необходимо преодолеть субстрату при реакции с внутриклеточным ферментом, связан с проникновением через внешнюю мембрану клетки. Например, в реакции получения L-аспарагиновой кислоты из фумарата аммония, катализируемой клетками Е. coli, реакция протекает с малой скоростью, если клетки предварительно не "активировать", проводя частичное разрушение внешней цитоплазматической мембраны [379].
Для описания кинетики реакций в клетках нами использовано представление о клетке как о мембранном микрореакторе [380, 381]. Развитая ниже кинетическая модель основана на следующих предположениях.
1. Массоперенос субстратов в клетку и продуктов из клетки осуществляется путем пассивной диффузии через внешнюю цитоплазматическую мембрану, которая обеспечивает основное сопротивление массопереносу. Транспортные механизмы в биологических мембранах достаточно сложны. В ряде случаев могут наблюдаться энергозависимые процессы переноса веществ против градиентов их концентраций. Однако широко распространены процессы, в которых перенос осуществляется по градиенту концентрации компонента. Это пассивный перенос с облегченной или затрудненной диффузией. В системах, в которых используются высокие внешние концентрации субстратов, этот транспортный механизм, по-видимому, играет наиболее важную роль [380-385].
2. В первом приближении считается, что фермент равномерно распределен по клетке. В общем случае на кинетику каталитического процесса с участием ферментов в клетках может оказывать влияние один из следующих эффектов: а) внешнедиффузионный перенос субстрата из объема к поверхности клетки; б) перенос субстрата и продукта через внешнюю мембрану; в) внутридиффузионный перенос субстрата и продукта в клетке. Очевидно, что в зависимости от условий проведения процесса любой из этих эффектов может определять скорость реакции в целом.
В различных экспериментальных условиях можно элиминировать влияние тех или иных эффектов на скорость реакции. Влияние внешнедиффузионного переноса может быть исключено путем эффективного перемешивания суспензии клеток с реагентами. При этом система будет переведена в режим, когда экспериментально наблюдаемая скорость процесса не зависит от скорости перемешивания раствора. В этих условиях происходит "стирание" диффузионного слоя, и он не оказывает влияния на скорость процесса. Внешнедиффузионный перенос не оказывает влияния на скорость процесса также при использовании высоких концентраций субстрата, поскольку скорость переноса линейно зависит от концентрации компонента.
При высоких концентрациях фермента в клетке и высоких специфических активностях может реализоваться ситуация, когда на скорость процесса оказывает влияние торможение процесса диффузионным переносом внутри клетки. В этом случае распределение субстрата по клетке имеет специфический характер, при этом объем клетки обеднен субстратом [380]. Критерием отсутствия внутридиффузионного торможения являются низкие значения модуля Тиле. Так же как и для внешней диффузии, использование высоких "насыщающих" концентраций субстрата переводит систему в режим, в котором лимитирующей является максимальная скорость ферментативной реакции, и внутридиффузионными эффектами можно практически пренебречь.
Один из эффектов, который должен наблюдаться экспериментально, связан с переносом субстрата и продукта через внешнюю мембрану. Модель клеточного ферментативного процесса как реакции в мембранном микрореакторе учитывает именно этот эффект.
Для мембранного микрореактора математически задача сводится к решению и анализу решения уравнения
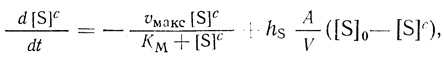 (2.109)
(2.109)которое вытекает из уравнения (2.107), где hS - проницаемость внешней мембраны для субстрата; [S]0 - концентрация субстрата во внешней среде; [S]c - концентрация субстрата в клетке.
Важно отметить, что системы с внешней диффузией, реактор идеального перемешивания и модель клетки как мембранного микрореактора математически изоморфны. Основное уравнение, описывающее изменение концентрации субстрата в зоне реакции, можно записать в виде
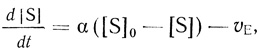 (2.110)
(2.110)где α = D/l для внешнедиффузионного переноса; α = u/V для безградиентного реактора (см. уравнение (2.107)); α = hA/V для мембранного микрореактора (см. уравнение (2.108)). В этом плане для кинетики действия ферментов в клетке можно использовать кинетические подходы, развитые для описания систем с внешней диффузией и для проточного безградиентного реактоpa [353, 378]. В частности, в стационарном состоянии отношении концентраций субстрата в клетке и среде дается уравнением
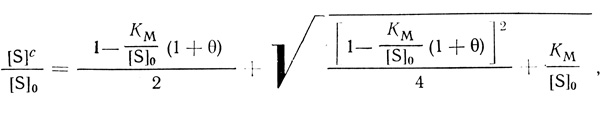 (2.111)
(2.111)вид которой определяется двумя безразмерными параметрами:
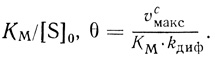 (2.112)
(2.112)По своему физическому смыслу модуль θ эквивалентен диффузионному модулю для внешней диффузии.
Анализ показывает, что если θ << 1, массоперенос через внешнюю мембрану не оказывает влияния на скорость процесса, [S]c/[S]0 = 1. При θ >> 1 и (KM/[S]0 > 1 реакция протекает в диффузионно-контролируемом режиме. Для ферментативных реакций в сферических клетках модуль θ может быть оценен из экспериментальных данных, если известны величины υмакс, КМ, проницаемость клеточной мембраны hS и радиус клетки R:
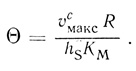 (2.113)
(2.113)Коэффициент каталитической эффективности зависит от [S]0/KM и Θ:
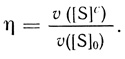 (2.114)
(2.114)При низких значениях концентраций субстрата ([S]0/KM) < 1 коэффициент эффективности обратно пропорционален диффузионному модулю
η = 1/θ. (2.115)
Идеальной физической моделью мембранного микрореактора являются искусственные микрокапсулы с иммобилизованными в них ферментами. Методы получения микрокапсулированных ферментов и их свойства описаны в работах [386-388]. Кинетические особенности реакций в такого рода системах анализируются в работах [389, 390]. Кинетические закономерности ферментативных реакций в микрокапсулах и в клетках в первом приближении одинаковы.
В рамках модели мембранного микрореактора кинетику изменения концентрации компонентов в клетке описывает система дифференциальных уравнений:
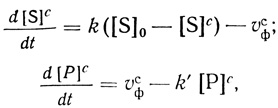 (2.116)
(2.116)где [S]c и [S]0 - концентрация субстрата в клетке и во внешней среде соответственно; [Р]с - концентрация продукта в клетке ([Р]вн ≈ 0); t - время; k и k'- константы скорости переноса субстрата в клетку и продукта из клетки; υфс - скорость ферментативного процесса в клетке. Константы скорости переноса субстрата и продукта определяются в соответствии с уравнением
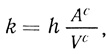 (2.117)
(2.117)где hS - проницаемость мембраны для субстрата (hР - для продукта); Ас - поверхность мембраны клетки; Vc - объем клетки. Для мембраны конечной толщины l проницаемость определяется как отношение коэффициента диффузии D к толщине мембраны. В зависимости от геометрии клетки (сфера, цилиндр, эллипсоид) константа скорости переноса будет иметь различный вид (табл. 24).

Таблица 24
Важный вывод проведенного анализа заключается в том, что в определенных условиях кинетическое описание реакции существенно упрощается, что позволяет сопоставить кинетические уравнения с экспериментом и определить ряд параметров действия фермента в клетке. В условиях, когда концентрация субстрата в клетке существенно превышает константу Михаэлиса (υф = υсмакс), кинетика накопления продукта в сферической клетке радиуса R описывается уравнением
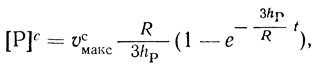 (2.121)
(2.121)где υсмакс - максимальная скорость ферментативной реакции в клетке. Экспериментально определяемое количество продукта дается уравнением
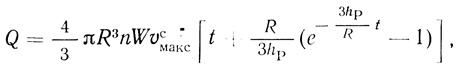 (2.122)
(2.122)где Q - количество продукта; n - концентрация клеток в суспензии; W - объем суспензии. На кинетической кривой продукт реакции - время должен наблюдаться период индукции, который определяется проницаемостью клеточной мембраны для продукта реакции:
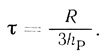 (2.123)
(2.123)В этих условиях стационарная скорость реакции не зависит от концентрации субстрата и дается уравнением
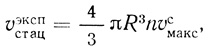 (2.124)
(2.124)где υэкспстац рассчитывается на единицу объема суспензии, а υсмакс - на единицу объема клеточной фазы. На основе экспериментально определяемых величин можно вычислить проницаемость клеточной мембраны для продукта реакции (hP) и среднюю стационарную концентрацию продукта в клетке:
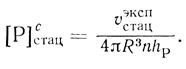 (2.125)
(2.125)
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'