
2. Кинетические закономерности реакции в полиферментных системах
Исследования механизмов полиферментных реакций весьма важны с точки зрения анализа процессов в системах биоконверсии энергии. Большой интерес вызывают системы, осуществляющие превращение различных органических соединений (углеводов, спиртов, органических кислот) в водород. Возможность проведения такого рода процессов обусловлена функционированием многостадийных полиферментных цепей.
На рис. 36 приведены данные по кинетике образования водорода в биферментной системе с участием гидрогеназы в качестве терминального фермента. Схему осуществленного процесса можно записать в виде
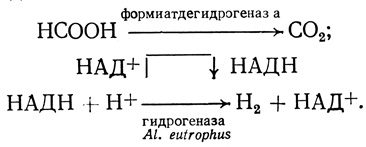
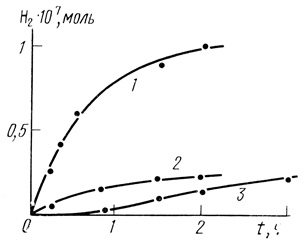
Рис. 36. Кинетика выделения водорода из формиата натрия в биферментной системе формиатдегидрогеназа - гидрогеназа. 0,3 М формиата; 1 мМ НАД; активность формиатдегидрогеназы 9 мкМ/мин⋅мл; pH 7,0; 0,05 М фосфата калия; 1 - 0,4 мл гидрогеназы; 2 - 0,2 мл гидрогеназы; 3 - 0,2 мл гидрогеназы без предварительной активации фермента дитионитом натрия
Теоретический предельный выход преобразования энергии путем получения водорода из формиата равен 99,4%. Для выявления общих и специфических черт реакций и создания количественного базиса их оптимизации следует выяснить количественные закономерности процессов в такого рода системах.
Важный класс реакций с участием многокомпонентных белковых систем представляют собой реакции переноса электрона. Фундаментальной особенностью биоэнергетических механизмов является осуществление окислительно-восстановительных реакций с участием белковых переносчиков электрона. Организация клеточных структур обеспечивает направленный перенос электронов от одних компонентов к другим, создавая своеобразные микротоки. Такого рода процессы играют определяющую роль в механизме трансформации световой энергии в энергию химических связей в фотосинтезе, в механизме трансформации энергии при аэробном дыхании.
Формально-кинетический анализ закономерностей процессов в полиферментных системах дан в работах [463-466]. Рассмотрены системы, в которых уравнение скорости, описывающее поведение каждого фермента цепи, дается уравнением Михаэлиса. Детально анализируются стационарные процессы в линейных цепях. Обсуждаются биферментные системы в стационарном режиме при постоянной концентрации исходного субстрата, дана оценка диапазона времени и условий протекания процесса в стационарном режиме, развиты методы определения кинетических параметров ферментов из данных по стационарной кинетике реакции, рассмотрены регуляторные особенности системы двух ферментов. Рассмотрена кинетика в линейных цепях ферментов, стационарная кинетика при постоянной концентрации исходного субстрата и в системе с учетом материального баланса по субстрату.
В работах [464-466] исследована нестационарная кинетика, предстационарный и релаксационный режимы в биферментной системе и линейных цепях. Основные результаты приведены в табл. 27.
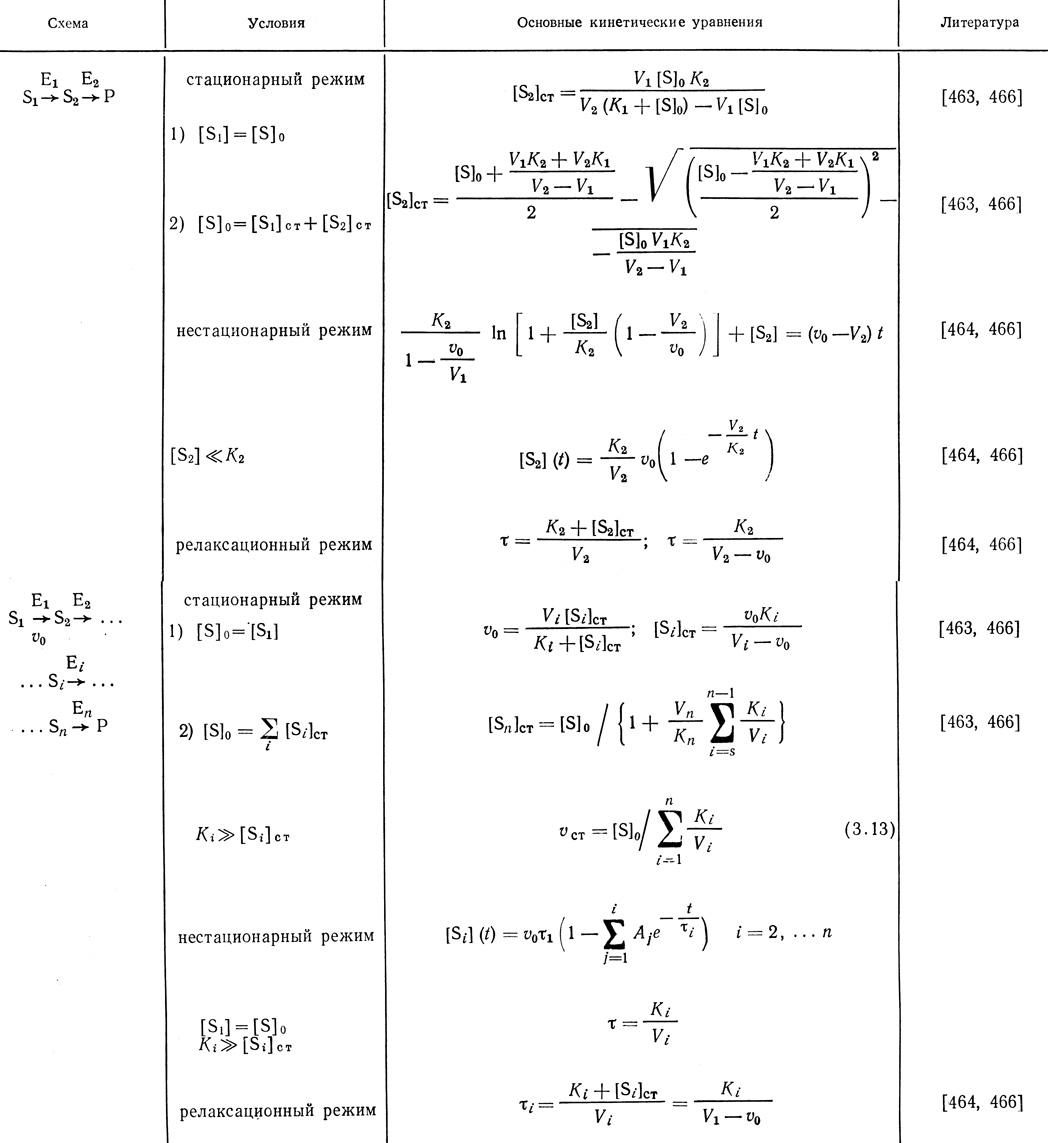
Таблица 27. Кинетические закономерности реакций в полиферментных системах
Некоторые выводы, полученные при исследовании кинетики реакций в полиферментных системах имеют весьма общий характер [15].
Анализ уравнения 3.13 (из табл. 27) приводит к выводу, что самое большое влияние на общую скорость процесса оказывают ферменты с наименьшей максимальной скоростью. Действительно, в сумму, составляющую знаменатель, наибольший вклад вносят члены, имеющие большое неблагоприятное значение константы Михаэлиса или наименьшую максимальную скорость. В пределе, если существует фермент, для которого отношение Ki/Vi много больше, по сравнению с другими ферментами, уравнение скорости приобретает вид
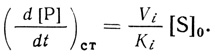 (3.14)
(3.14)В этих условиях скорость процесса в целом определяется кинетическими параметрами лишь одного, наиболее медленно работающего фермента. Этот важный вывод - весьма общий для теории сложных химических превращений, поскольку он позволяет говорить о лимитирующей стадии процесса. В условиях работы линейной полиферментной цепи при значительной глубине превращения исходного субстрата в промежуточные метаболиты и существенном различии в кинетических параметрах ферментов Vi/Ki скорость процесса в целом определяется наиболее медленной, лимитирующей стадией.
Возникает вопрос о критериях, которые позволяют определить, какая стадия сложного процесса должна быть лимитирующей. Уравнения (3.13) и (3.14) дают однозначный теоретический критерий определения лимитирующей стадии. Из уравнения (3.14) следует, что скорость процесса в целом линейно зависит от концентрации фермента, определяющего скорость реакции, и практически не зависит от концентрации остальных ферментов. Если экспериментально допустимо изменение в системе концентрации ферментов, этот подход можно использовать для определения лимитирующей стадии реакции. Изменить в системе концентрацию активного фермента и соответственно скорость данной стадии реакции в некоторых случаях можно путем непосредственной вариации концентрации фермента. Более общий подход заключается в применении различных обратимых и необратимых специфических ингибиторов ферментов.
При увеличении скорости наиболее медленной стадии или, наоборот, уменьшении скорости быстрой стадии может происходить смена лимитирующей стадии (рис. 37). Если в общую скорость реакции наибольший вклад вносят два наиболее "плохо" работающих фермента, уравнение скорости имеет вид
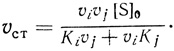 (3.15)
(3.15)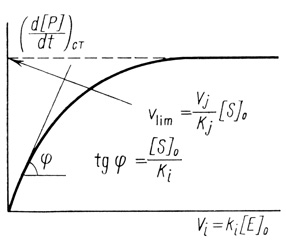
Рис. 37. Смена лимитирующей стадии в процессе изменения концентрации фермента, лимитирующего процесса на начальном участке
В условиях υiKj << υjKi скорость процесса определяется i-й стадией реакции. В этой области наблюдается линейная зависимость скорости процесса от концентрации i-го фермента. В области соизмеримых значений υiKj и υjKi оба фермента вносят вклад в скорость процесса и наблюдается отклонение от линейной зависимости процесса от концентрации i-го фермента. И наконец, в условиях υiKj >> υiKj скорость реакции не зависит от концентрации фермента Ei и лимитирующей становится j-я стадия превращения субстрата.
Рассмотрим работу линейной полиферментной цепи при широкой вариации активности одного из ее ферментов. Предположим, что в исходном состоянии система работает в режиме, когда υi >> υ0 для каждого из ферментов цепи. Это приводит к тому, что концентрации промежуточных метаболитов, установившиеся в стационарном состоянии, будут меньше констант Михаэлиса соответствующих ферментов, осуществляющих превращение данного субстрата. Если мы начнем ингибировать один из ферментов цепи, скорость реакции расхода данного промежуточного метаболита будет падать. Однако, если в этих условиях будет выполняться неравенство υi >> υ0, это не скажется на общей скорости реакции. Уменьшение скорости расхода промежуточного субстрата автоматически приведет к увеличению его стационарной концентрации, что даст увеличение скорости процесса на данной стадии. Скорость превращения промежуточного метаболита автоматически подстроится под общую скорость реакции, которая будет определяться скоростью первой стадии (υст = υ0).
Если увеличить степень ингибирования данного фермента настолько, что неравенство υi >> υ0 выполняться не будет, увеличение концентрации промежуточного метаболита достигнет такого уровня, что его концентрацию необходимо учитывать в уравнении материального баланса по субстрату. В этом режиме (при условии [Si]ст << Ki) кинетика реакции описывается уравнением типа (3.13) и начинает появляться зависимость скорости процесса от концентрации ингибируемого фермента. При существенном уменьшении активности этого фермента скорость реакции будет лимитироваться превращением данного метаболита.
В работе [260] дан статистический анализ известных в литературе данных по величинам kкат и показано, что наиболее вероятны значения констант скоростей лимитирующих стадий лежат около 102 с-1. Можно ожидать, что эта величина является характеристикой лимитирующих стадий в полиферментных реакциях.
Таким образом, проведенный выше анализ позволил количественно сформулировать представление о лимитирующей стадии процесса в полиферментной линейной цепи и дать критерии, позволяющие определить лимитирующую стадию.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'