
Кинетическая теория инактивационных процессов в биологических системах
Вероятность того, что какая-либо система будет безотказно работать в течение определенного промежутка времени, можно характеризовать численной величиной. Задачей теории надежности физических систем является расчет вероятности безотказной работы элемента (или системы элементов) в течение заданного промежутка времени. Эта вероятность в общем случае - функция времени и носит название функции надежности Р(t) [506]. Соответственно вероятность отказа (выхода из строя, потери функциональной активности) описывается функцией
Q(t) = 1 - Р(t). (3.59)
Предположим, что вероятность безотказной работы элемента в период от нуля до t задана величиной P(t), а вероятность того, что элемент будет работать в следующем интервале времени Δt - величиной Р(Δt). В этом случае вероятность того, что элемент будет работать безотказно в полном диапазоне от нуля до t+Δt, дана произведением двух вероятностей:
P (t + Δt) = P(t) P(Δt). (3.60)
Вероятность отказа вывода из строя элемента в этом диапазоне времени при Δt → 0 дана функцией
| Q(Δt) ≈ - | P'(t) Δt | . (3.61) |
| P(t) |
Если ввести обозначение
-P'(t)/P(t) = λ(t), (3.62)
уравнение (3.61) принимает вид
Q(Δt) = λ(t)Δt. (3.63)
Таким образом, введенный параметр λ(t) характеризует вероятность отказа элемента на каждом заданном промежутке времени. Параметр λ(t) - важная характеристика надежности, которой мы часто будем пользоваться в дальнейшем. Параметр λ(t) носит название опасности или интенсивности отказов, имеет размерность обратного времени. По физическому смыслу интенсивность отказов представляет собой частоту отказов.
Для большинства физических систем интенсивность отказов имеет вид функции, представленной на рис. 46 [506]. Условно весь интервал времени работы системы можно разбить на три участка. На первом участке интенсивность отказов элементов повышена. В течение этого интервала времени выходят из строя наиболее "дефектные" элементы. В дальнейшем интенсивность отказов обычно выходит на постоянный уровень. Это "рабочий" период, в котором с постоянной частотой происходит выход из строя элементов. В процессе работы в системе накапливаются необратимые дефекты, элементы в силу ряда физико-химических процессов "стареют" и при этом увеличивается интенсивность отказов (период 3).
![Рис. 46. 'Классический' вид зависимости интенсивности отказов от времени в физических системах [506]](pic/000245.jpg)
Рис. 46. 'Классический' вид зависимости интенсивности отказов от времени в физических системах [506]
Дифференциальное уравнение (3.62) дает связь между функцией надежности и интенсивностью отказов и может быть решено относительно функции надежности
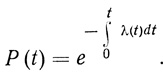 (3.64)
(3.64)Соответственно вероятность безотказной работы элемента в любом интервале времени t1, t2 дается уравнением
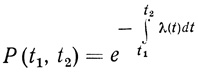 (3.65)
(3.65)Уравнения (3.64) и (3.65) - наиболее важные уравнения теории надежности. При известной функции интенсивности отказов они дают возможность рассчитать вероятности безотказной работы любой системы в заданном интервале времени. Эти уравнения являются кинетическими, описывают поведение системы во времени.
Экспериментально функцию надежности можно достаточно просто определить, если имеется возможность провести испытание и найти, как во времени изменяется число работоспособных элементов. Если число работоспособных элементов во времени дается функцией n(t), эмпирическая функция надежности выражается уравнением
PN(t) = n(t)/N0, (3.66)
где N0 - число работоспособных элементов в начальный момент времени. При большом числе элементов и испытаний эмпирическая функция PN(t) с достаточной степенью приближения описывает функцию P(t).
В энзимологии функция надежности непосредственно связана с кинетикой инактивации фермента или системы ферментов. Построение эмпирических функций надежности основано на определении числа элементов n(t), сохранивших работоспособность к данному моменту времени (см. уравнение (3.66)). В применении к задачам энзимологии n(t) - число молекул фермента, сохранивших каталитическую активность к моменту времени t. Если скорость ферментативной реакции (или определяемая на опыте активность фермента) пропорциональна числу активных молекул биокатализатора
A(t) = αn(t), (3.67)
то в соответствии с уравнением (3.66) эмпирическая функция надежности задается функцией
P(t) = A(t)/A0, (3.68)
где А0 - активность фермента (или системы ферментов) в начальный момент времени. Таким образом, исследование зависимости изменения во времени активности фермента позволяет построить эмпирическую функцию надежности.
Важным количественным параметром надежности работы элемента или системы элементов является среднее время безотказной работы, которое определяется формулой
T0 = ∫0∞ P(t) dt. (3.69)
Среднее время безотказной работы, заданное числовой величиной, - удобная характеристика надежности элемента и системы, графически определяется как площадь под кривой P(t). Уравнение (3.69) дает общий количественный критерий при сравнении систем, инактивирующихся по различным механизмам.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'