Экспоненциальный закон надежности в кинетике инактивации ферментов

Как видно из рис. 46, для большинства систем можно выделить период времени, в течение которого интенсивность отказов постоянна:

Если интенсивность отказов в данном промежутке времени постоянна и не является функцией времени, то согласно уравнению (3.64) функция надежности имеет вид

Этот экспоненциальный закон весьма широко применяется в теории надежности.

Очевидно, что опасность отказа λ в этом случае имеет смысл константы скорости инактивации фермента k и связана с определенным физико-химическим процессом в активном центре фермента, приводящим к потере каталитической активности.

Таким образом, показатель экспоненты в уравнении (3.70) допускает два толкования. С точки зрения химической кинетики - это константа скорости мономолекулярной реакции превращения фермента Е в неактивную форму Е_i, в терминах теории надежности - интенсивность отказов. Очевидно, что по физическому смыслу эти понятия эквивалентны и представляют собой частоту элементарных актов инактивации молекул фермента.

Среднестатистическое время работы всех молекул катализатора, инактивирующегося по экспоненциальному закону, равно

Применение теории надежности позволяет очень просто сделать ряд важных качественных выводов о кинетических закономерностях инактивации сложных полиферментных систем. В работах [466, 505] рассмотрены кинетические закономерности инактивации полиферментных систем в предположении, что каждый из ферментов инактивируется по экспоненциальному закону.

Рассмотрим полиферментную систему с участием n ферментов, инактивирующихся по экспоненциальному закону. Для полиферментных систем, осуществляющих превращение исходного субстрата до конечного продукта реакции, инактивация любого из ферментов ведет к потере каталитической функции всей системы. Если ферменты инактивируются независимо друг от друга, вероятность безотказной работы всей системы в целом будет равна произведению вероятностей безотказной работы каждого фермента цепи в отдельности. Функция надежности имеет вид

Если инактивация каждого фермента происходит с интенсивностью

P_i(t) = e^-λ_it, (3.73)

подстановка уравнения (3.73) в уравнение (3.72) приводит к функции

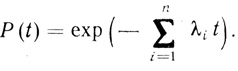(3.74)

Среднее время работы будет иметь вид

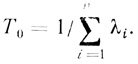(3.75)

Наибольший вклад в сумму (знаменатель этого уравнения) вносят наиболее быстрые кинетические процессы инактивации, и, таким образом, среднее время безотказной работы полиферментных систем определяется устойчивостью наиболее лабильных белков. Если в цепи ферментов есть лабильный белок, инактивирующийся быстрее, чем остальные белки полиферментной системы, инактивация именно этого фермента и будет проявляться в кинетике инактивации всей системы.

Рассмотрим систему параллельно работающих ферментов, катализирующих одну и ту же реакцию и инактивирующихся с различными скоростями. Для случая произвольного числа фракций фермента, различающихся активностью и стабильностью, анализ соответствующей функции надежности приводит к уравнению

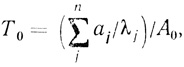(3.76)

где a_j, λ_j - начальные активности и константы скорости инактивации каждой фракции фермента соответственно; А₀ - сумма начальных активностей или регистрируемая каталитическая активность системы в начальный момент времени.

Важно отметить, что среднее время безотказной работы системы параллельно работающих ферментов определяется наиболее активной (наибольшей a_j) или наиболее стабильной (наименьшей λ_j) фракцией фермента. Это отличает данную систему от системы последовательно работающих катализаторов, в которой надежность определяется наиболее лабильным белком.

Ферменты, объединенные в системы и осуществляющие цепь последовательных превращений субстратов, в общем случае обладают различной устойчивостью к инактивирующим воздействиям. В силу этого в процессе инактивации полиферментной системы может происходить смена лимитирующей стадии. Представим себе, что наиболее медленно работающий фермент, скорость реакции с которым определяет активность всей системы в целом, достаточно устойчив. При этом, если один из ферментов цепи быстро теряет свою активность, возникает ситуация, когда скорость процесса определяется активностью именно этого, наиболее лабильного фермента. Таким образом, по мере инактивации системы происходит смена лимитирующей стадии. Это должно накладывать отпечаток на кинетику инактивации.

Рассмотрим линейную полиферментную цепь. Согласно анализу [466] в определенных условиях стационарная скорость процесса с участием n ферментов описывается уравнением

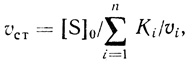(3.77)

где [S]₀ - начальная концентрация первого субстрата; υ_i, K_i - максимальная скорость и константа Михаэлиса каждого участка цепи. Рассмотрим случай, когда в цепи есть два фермента, обладающих максимальными и соизмеримыми кинетическими параметрами K_i/υ_i. Если величины параметра K_i/υ_i для остальных ферментов цепи существенно меньше величины этого параметра для двух ферментов, уравнение стационарной скорости будет иметь вид

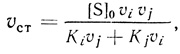(3.78)

где индексы i и j характеризуют параметры каждого фермента.

Предположим, что инактивация обоих ферментов происходит по экспоненциальному закону, т. е. каждый фермент инактивируется с постоянной во времени интенсивностью отказов λ_i и λ_j. Функция надежности имеет вид

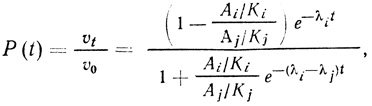(3.79)

где A_i = k_{кат, i}[E_i]₀.

Кинетическое поведение системы в процессе инактивации определяется отношением кинетических параметров

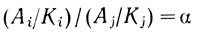(3.80)

и разностью интенсивностей отказов двух ферментов. Рассмотрим три наиболее важных частных случая:

1. Частоты отказов обоих ферментов цепи равны между собой

Функция надежности имеет вид

Кинетика процесса определяется интенсивностью отказов любого из ферментов вне зависимости от того, какой фермент лимитирует скорость полиферментной реакции. Это самый простой случай.

2. Процесс лимитируется j ферментом цепи, который инактивируется существенно быстрее остальных. Это соответствует условиям

Функция надежности дается уравнением

Кинетика инактивации системы имеет экспоненциальный характер. Надежность и среднее время работы системы определяется интенсивностью отказов лимитирующего скорость фермента.

3. Существенно быстрее инактивируется фермент, который не лимитирует скорость реакции. С формальной точки зрения это соответствует условиям: α >> 1, λ_i >> λ_j, использование которых модифицирует уравнение (3.79) к виду

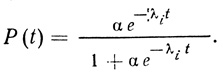(3.85)

Кинетическая кривая инактивации имеет более сложный вид и определяется интенсивностью отказов фермента, не лимитирующего скорость полиферментной реакции (рис. 47). Среднее время работы всей системы в целом дается уравнением

и соответствует времени, в течение которого активность системы падает вдвое.

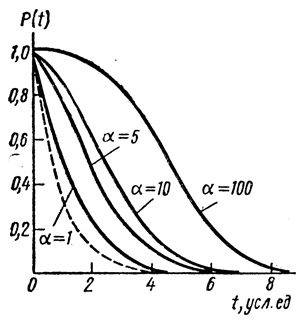
Рис. 47. Кинетика инактивации системы со сменой лимитирующей стадии. Интенсивность отказов условно принята равной единице

Смена лимитирующей стадии может иметь место и при инактивации систем, работающих в диффузионном режиме. С учетом эффектов диффузионного слоя стационарная скорость реакции имеет вид

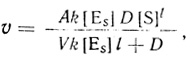(3.87)

где k - поверхностный эквивалент константы k_кат/K_М. В предположении, что фермент инактивируется по экспоненциальному закону, функция надежности дается уравнением

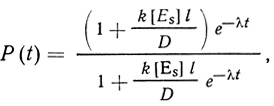(3.88)

где λ - интенсивность отказов иммобилизованного фермента. Если в начальный момент времени система работает в строго диффузионном режиме (k[E_S]l/D >> 1), среднее время работы системы дается уравнением

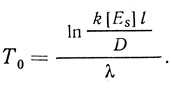(3.89)