Нормальный закон надежности при инактивации ферментов и полиферментных систем

Применимость экспоненциального закона надежности зависит от характера отказов элемента. Как показано выше, внезапные случайные отказы, приводящие к полной потере биокаталитической функции по принципу "все или ничего", довольно хорошо описываются экспоненциальным законом. В этом случае элементарный акт инактивации связан с внезапной и полной потерей молекулой фермента каталитической активности.

В ряде случаев кинетические закономерности инактивации биологических катализаторов и биосистем достаточно сложны и не описываются простым экспоненциальным законом надежности. Это относится, прежде всего, к сложным объектам, включающим различные ферменты, белки и биомембраны. В комплексной молекулярной организации биологических структур могут протекать необратимые физико-химические изменения, которые не проявляются сразу в изменении активности. Только постепенные накопления такого рода "скрытых" дефектов способны привести к необратимым последствиям с потерей биологической функции. По-видимому, в биологических системах такой механизм "старения" весьма распространен.

В теории надежности отказы, возникающие в результате необратимых физико-химических изменений структуры, которые не приводят к потере функции, а носят характер "скрытых ошибок", называют постепенными отказами. Анализ показывает, что процесс "старения" биологических объектов нередко имеет характер постепенных отказов и весьма хорошо может быть описан в терминах теории надежности с использованием нормального закона.

Для нормального закона функция надежности (при σ << Т₀) имеет вид [506]

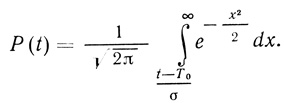(3.90)

На рис. 48 приведен вид функций P(t), вычисленных с использованием уравнения (3.90). Параметр Т₀ определяет период времени, в течение которого вероятность безотказной работы элемента (или системы) уменьшается в два раза. Как следует из уравнения (3.90), при t = T₀ величина Р(Т₀) равна 0,5.

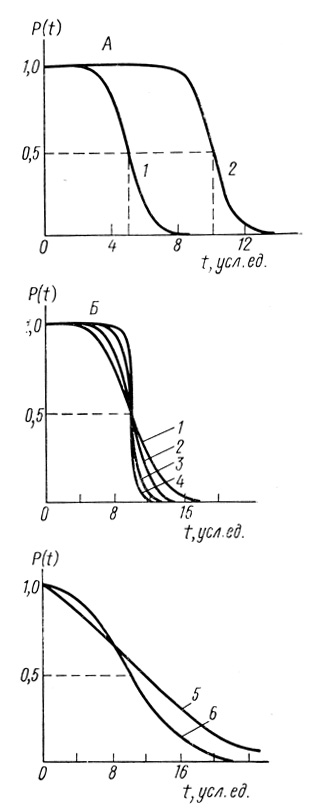
Рис. 48. Нормальный закон надежности. А - σ = 1; 1 - Т₀ = 5 усл. ед; 2 - Т₀ = 10 усл. ед.; Б - Т₀ = 10 усл. ед. σ: 1 - 3,0; 2 - 2,0; 3 - 1,0; 4 - 0,5; 5 - 5,0; 6 - 10,0

Параметр σ связан с дисперсией времени жизни элементов и различны параметрами σ в условиях σ << Т₀. В условиях σ << T₀ кривые симметричны относительно прямых t = T₀ и Р = 0,5.

Таким образом, кинетические кривые инактивации с большими периодами индукции могут быть отражением двух механизмов: 1) сменой лимитирующей стадии в процессе инактивации системы (см. выше); 2) постепенным накоплением скрытых дефектов, происходящим по нормальному закону, приводящему к необратимому "старению" системы. Экспериментальные критерии, которые позволили бы различить эти два механизма инактивации, отсутствуют. Можно считать, что система инактивируется по нормальному закону, если показано, что в процессе инактивации не происходит смена лимитирующей стадии в реакции, по которой определяется активность системы.

При анализе стабильности биологических структур достаточно часто встречаются системы, инактивирующиеся по нормальному закону.

Возможно, что инактивация гидрогенезы Al. eutrophus на воздухе (см. рис. 45) протекает по механизму накопления скрытых дефектов.

Из общих соображений можно предположить, что постепенные отказы должны иметь место в комплексных структурированных системах, включающих биомембраны. Это относится, прежде всего, к целым клеткам или органеллам. На рис. 44 приведены данные по изменению во времени фотосинтетической активности клеток синезеленых водорослей An. variabilis. Фотосинтетическую активность популяции клеток измеряли по скорости фотохимического восстановления феррицианида при постоянной концентрации клеток, и данные, приведенные на рис. 44, фактически представляют собой изменение скорости фотосинтеза в расчете на одну клетку водоросли. Кривая рассчитана теоретически по уравнению (3.90) при использовании соответствующих параметров Т₀. Видно, что экспериментальные данные достаточно хорошо описываются этим уравнением. Важно подчеркнуть, что весьма сложный процесс "старения" фотосинтезирующих клеток хорошо объясняется простыми физическими представлениями о случайном характере появления ошибок и постепенности отказов в сложной биологической системе.

Таким образом, развитая на основе представлений надежности кинетическая теория инактивации ферментов в биологических системах описывает и объясняет все типы кинетических кривых инактивации, наблюдаемых в системах биофотолиза воды.