Обобщение метода Гайтлера-Лондона. Создание теории спиновой и орбитальной валентности

После объяснения на основе квантовой механики природы химической связи в молекуле водорода были предприняты многочисленные попытки обобщить подход Гайтлера-Лондона на более сложные молекулы, что привело к созданию метода валентных связей. Хотя последний и не является оптимальным для проведения количественных расчетов, он существенно повлиял на развитие квантовой теории химической связи и валентности, что обусловило его необычайно широкую популярность среди ми ков.

В 20-30-х годах метод ВС разрабатывали в основном немецкие, американские и советские теоретики, среди которых следует назвать имена Гайтлера, Лондона, Вейля, Теллера, Борна, )линга, Слэтера, Ю. Б. Румера и др. При этом получили звитие различные направления: одни ученые разрабатывали авным образом математические вопросы теории многоэлектронных систем (Гайтлер, Румер, Вейль, Лондон, Слэтер, Борн), другие - сосредоточили свое внимание на развитии физико-химических основ теории (Полинг, Слэтер). Центром математического направления был Геттинген. И не случайно. Геттингенский университет представлял собой тогда один из крупнейших научных центров мира, особенно в области математики и теоретической физики. С Геттингеном связано творчество таких выдающихся ученых, как Клейн, Гильберт, Вейль, Минковский, Нетер, Борн и многих других.

На развитии математики в Геттингенском университете следует остановиться особо. Начиная с 60-х годов XIX в. центр тяжести математических исследований постепенно переносится с теории функций на другие области математики и прежде всего на алгебру. В начале XX в. процесс алгебраизации геометрии, топологии, некоторых классических глав анализа принимает особенно интенсивный характер.

Важнейшим направлением научного творчества многих гет-тингенских математиков и физиков-теоретиков становится теория групп. Во второй половине XIX - начале XX вв. немецкие ученые занимали лидирующее положение в этой области математики. В работах Шура, Фробениуса, Гордана и других были заложены основы теории представлений. Именно в Германии раньше, чем где-либо, была понята важность теоретико-групповых концепций для физики и в первую очередь для ее новых разделов-теории относительности и квантовой механики. Для квантовой химии это обстоятельство имело большое значение, ибо в период, когда еще не были разработаны эффективные приближенные способы решения многоэлектронной задачи, теория групп давала надежный и мощный метод исследования молекулярных систем. Однако далеко не все физики-теоретики того времени были знакомы с теорией групп и понимали необходимость ее изучения. Работы геттингенских ученых часто называли "групповой чумой" (gruppenpest). Большую роль в распространении теоретико-групповых концепций в квантовой механике сыграли монографии Вейля [85] и Вигнера [8].

В квантовую химию сначала проникла теория групп перестановок, а позже, примерно с 1932 г., в рамках метода МО стали учитывать пространственную симметрию молекулы. Такая последовательность естественна, так как при обобщении метода Гайтлера-Лондона на многоэлектронные системы необходимо было прежде всего уметь строить правильные (с точки зрения принципа Паули) волновые функции системы. Первые шаги в этом направлении были сделаны Гайтлером [48] и Лондоном [60, 61]. Остановимся сначала на работе Гайтлера.

Объектом исследования являлся некоторый атом А, взаимодействующий с другим атомом В (или системой атомов). Как А, так и В обладают по п валентных электронов каждый. Предполагалось, что вырождение в рассматриваемой многоэлектронной системе АВ имеет исключительно обменную природу, т. е пространственное и резонансное вырождение отсутствуют^*. Это означает, в частности, что А и В представляют собой либо тождественные, либо различные, но находящиеся в одинаковых квантовомеханических состояниях системы.

^* (При этом Гайтлер, как и в работе [50], обращает внимание на существенное различие между понятием резонансного вырождения и вырождения обменного. "Резонанс имеет место, если рассматриваются два атома водорода, первый из которых находится в основном состоянии, а второй возбужден. Общая энергия системы не изменится, если первый атом возбудится до того состояния, в котором находился второй, а тот, в свою очередь, перейдет в основное состояние. Каждый электрон остается при этом около своего ядра. Об обмене здесь нет и речи" [48, с. 838]. Таким образом, Гайтлер, в отличие от Полинга [72, с. 1368], строго разделял понятия резонанса и обмена.)

Электроны каждой из систем А и В находятся в различных одноэлектронных (бесспиновых!) состояниях, т. е. описываются волновыми функциями, зависящими только от пространственных, но не спиновых переменных. При этом электроны дважды занятых состояний, соответствующие замкнутым оболочкам, не рассматриваются. "Существенной особенностью системы АВ по сравнению с молекулой водорода,- отмечает Гайтлер,- является то, что даже при отсутствии взаимодействия между А и В состояния этих многоэлектронных подсистем могут характеризоваться несколькими термами, подобно тому, как, например, конфигурации 1s2s атома Не соответствуют два терма: синглетный (¹S) и триплетный (³S)"[48, с. 838]. В зависимости от того, в каком состоянии находились А и В до их сближения, между ними осуществляются взаимодействия различного рода: либо притяжение и образование стабильной молекулы, либо отталкивание.

Это взаимодействие, как показал Гайтлер, можно оценить в первом приближении теории возмущений, решая уравнение

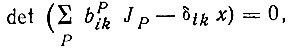(3.8)

где Р - перестановки 2n-электронов, образующие некоторую группу S_2n; b_ik - матричные элементы некоторого ортогонального неприводимого представления этой группы, реализованного на многоэлектронных функциях определенного терма; J_P - параметры возмущения, соответствующие обмену электронов между двумя одноэлектронными бесспиновыми состояниями; δ_ik - символ Кронекера; х - обусловленная возмущением поправка к энергии (в первом приближении). При этом Гайтлер специально отмечает, что он будет "проводить вычисление возмущений только для таких систем А и В, каждой из которых соответствуют антисимметричные термы" [48, с. 848]. Однако речь здесь идет об антисимметрии относительно перестановок только пространственных координат. Далее Гайтлер отмечает, что "представление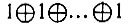^* для А или В означает, что эти системы имеют полностью антисимметричные термы" [48, с. 850]. Но при этом возникает вопрос: какому спиновому состоянию отвечает такой антисимметричный терм? Поскольку принцип Паули в его общей формулировке не принимался во внимание, то и ясного, обоснованного ответа на этот вопрос не было. Фактически Гайтлер просто воспользовался результатом работы [50], согласно которому антисимметричной координатной функции молекулы Н₂ соответствует триплетное состояние (параллельные спины). Применительно к системам А и В это означало, что каждая из них имеет несколько неспаренных электронов, "но это,- замечает Гайтлер,- как раз и есть тот случай, когда мы можем ожидать образование молекулы" [48, с. 848].

^* (Говоря современным языком, одномерное неприводимое представление группы перестановок, которому соответствует схема Юнга [1 N].- Прим. авт.)

Перестановки электронов внутри системы А или В мы, следуя работе [48], будем обозначать далее буквой R, прочие перестановки (между А и В) - буквой Q. Соответственно можно различать параметры J_Q И J_R.

Основным допущением теории Гайтлера является предположение, что J²_Q гораздо меньше J²_R, и потому J²_Q можно пренебречь, учитывая только члены, линейные по J_Q. Такое допущение для равновесного межъядерного расстояния может оказаться довольно грубым. Поэтому можно было надеяться лишь на то, что теория даст правильный порядок величины энергии диссоциации. Упрощая секулярное уравнение (3.8), Гайтлер получил для энергии диссоциации выражение

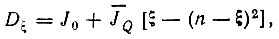(3.9)

где квантовое число ξ пробегает значения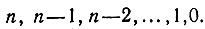

Параметр J₀ представляет собой кулоновский интеграл, а 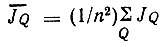- среднее значение обменного интеграла, характеризующее взаимодействие А и В.

Согласно Гайтлеру, в рассматриваемом случае, как и в случае взаимодействия двух атомов водорода, величина 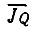отрицательна и при не слишком малых расстояниях преобладает над J₀^*. Кроме того, можно надеяться, что для различных взаимодействующих атомов рассматриваемые интегралы имеют не только одинаковый (отрицательный) знак, но и общий порядок величины. Тогда в зависимости от знака коэффициента 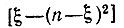при обменном интеграле 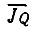следует ожидать либо притяжения атомов вплоть до образования ими устойчивой молекулы, либо их отталкивания. В первом случае указанный множитель должен быть положительным, во втором - отрицательным. В частности, основному состоянию соответствует ξ = n и наибольшая прочность связи, так как при этом D_ξ принимает наименьшее (с учетом знака) значение:

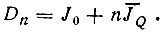(3.10)

^* (При уменьшении межъядерного расстояния содержащийся в J₀ член отталкивания атомных ядер возрастает и становится определяющим.)

Обсуждаемое состояние (ξ = n) коррелирует с теми термами изолированных А и В, для которых спиновые моменты электронов одной системы (А или В) антипараллельны спиновым моментам другой (В или А).

Кроме состояния с ξ = n могут существовать и состояния с меньшими ξ. Например, в таких соединениях азота, как N₂, NH₃ и т. п., имеется по три валентных электрона в незамкнутой оболочке атома N. Эти три электрона могут соответствовать квартетному состоянию, причем именно это состояние наивысшей мультиплетности по спину является основным для изолированного атома. При учете взаимодействия двух атомов азота или одного атома азота с тремя атомами водорода множитель при 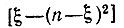может принимать четыре значения: +3, +1, -3, -9, которые определяются значениями ξ = 3, 2, 1,0.

Гайтлер не определял численное значение J_Q, он лишь качественно представил кривые энергии взаимодействия D_ξ (R) для молекулы N₂ (рис. 12).

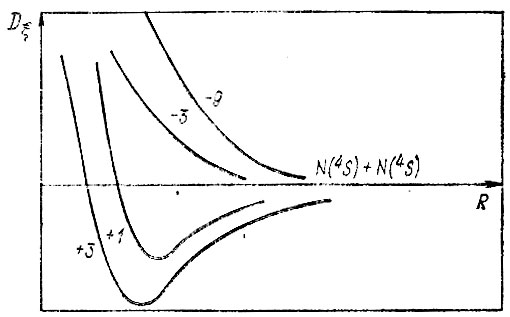
Рис. 12. Кривые энергии взаимодействия атомов D_ξ (R) для молекулы N₂ по Гайтлеру

Независимо от Гайтлера аналогичный подход был развит Лондоном, работы которого [60, 61] отличались, по существу, лишь более детальным изложением вопроса, а также более подробным исследованием химических примеров. В частности, им была установлена связь между валентностью атома и его спектроскопической мультиплетностью (магнитной тонкой структурой). По определению Лондона, валентность атома равна полному электронному спину в единицах ^h/₂ и поэтому на единицу меньше мультиплетности рассматриваемого атомного состояния [61, с. 49]. Кроме того, Лондон указал на возможность спектроскопического определения кратности ковалентной химической связи.

Пусть атомы характеризуются валентностью V₁ и V₂ и, следовательно, мультиплетностью по спину M₁ = V₁ + 1 и М₂ = V₂ + 1. Если при взаимодействии атомов связываются по одной валентности каждого атома, то в молекуле остается V(1) = V₁ + V₂ - 2 свободных валентностей и ее спиновая мультиплетность M(1) = M₁ + M₂ -3 (в круглых скобках указана кратность связи). В случае двойной связи V(2) = V₁ + V₂ - 4 и М(2) = M₁ + М₂ - 5.

В общем случае j-кратной связи

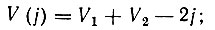(3.11)

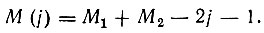(3.12)

Равенство j нулю означает отсутствие валентной связи.

Изложенный выше формализм, развитый независимо Гайтлером и Лондоном в 1927-1928 гг., интерпретирует понятие валентности как число спиновых моментов, спаренных при образовании молекулы. Однако в рамки этого формализма не укладывались молекулы, основное состояние которых является триплетным (В₂, O₂ и др.)" Так, в случае молекулы В₂ спаривания спиновых моментов электронов не происходит и, согласно (3.11), химическая связь вообще не должна образовываться. В связи с этим можно было бы повторить слова Хаксли, видевшего великую трагедию науки "в умерщвлении прекрасной теории мерзким фактом". Однако приведенные примеры, на наш взгляд, указывают не на ошибочность концепции спин-валентности, а на необходимость дополнения ее концепцией орбитальной валентности*. Идеи, позволившие осуществить такое обобщение^* были впервые высказаны Гайтлером в июне 1929 г. [49] и явились естественным обобщением созданной им и Лондоном теории ковалентной связи.

^* (В 30-х годах употребляли также термин l (или р)- валентность.)

"Прежняя теория валентности,- писал Гайтлер,- рассматривала лишь те случаи, когда имело место только обменное вырождение. Однако для галогенов и элементов группы кислорода^* это уже не верно. Их основным состоянием является Р-состояние, что говорит о наличии вырождения по магнитному квантовому числу. Расчеты автора показывают, что учет этого вырождения приводит к величине энергии связи между моментами количества движения l (bahnimpulsen l) того же порядка, что и энергия обмена. Вероятно, эта энергия также ответственна за образование молекул. Кроме рассматривавшейся ранее спин-валентности существует еще другой вид валентности (line zweite Arte Valenz)- l-валентность для атомов с l>0. При этом могут насыщаться только валентности одинакового вида. Вероятно, здесь мы имеем более сложные соотношения, чем в случае спиновых валентностей" [49, с. 547]. В качестве примера использования концепции орбитальной валентности обратимся к молекуле В₂. Атом бора в основном состоянии характеризуется электронной конфигурацией 1s²2s²2p и термом ²Р. В соответствии с этим электронную структуру молекулы В2 можно было бы описать двухэлектронной функцией Гайтлера-Лондона, составленной, однако, из р-орбиталей атома бора^**. Спариванию одноэлектронных спиновых моментов соответствовало бы расщепление молекулярного терма на два - синглетный и триплетный - согласно схеме

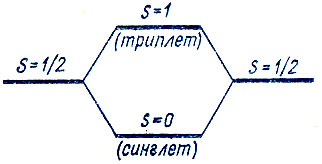
причем в соответствии с теорией Гайтлера и Лондона основному состоянию должен соответствовать синглетный терм. Но, как известно, основное состояние молекулы В₂ является триплетным, и поэтому указанный подход не применим. Образование химической связи в молекуле В₂ объясняется не спариванием спиновых моментов, а, очевидно, другими причинами. Для определения этих причин обратимся к идее Гайтлера о том, что образование связи обусловлено расщеплением вырожденных атомных термов при химическом взаимодействии, но не будем предполагать, что это вырождение является вырождением по спину. Так, для молекулы В₂ наряду с рассмотренным выше взаимодействием спиновых моментов может осуществляться взаимодействие орбитальных моментов по схеме

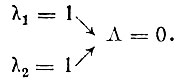
Здесь квантовые числа λ и Λ определяют абсолютную величину проекции момента импульса на ось молекулы. Так как рассматривается триплетное (по спину) состояние молекулы, принцип Паули и соображения симметрии требуют учета лишь значения λ = 1; т. е. дважды вырожденных 2pπ-орбиталей. Состояние с S = 1 и Λ = 0 соответствует ³∑-терму молекулы В₂. Реализация именно этого терма означает, что расщепление атомных ²P-термов вследствие спаривания орбитальных моментов (λ = 1) больше, чем расщепление, обусловленное спариванием спиновых моментов.

^* (Также и для других р-элементов.- Прим. авт.)

^** (При этом можно исключить из рассмотрения 1s- и 2s-электроны, полагая, что они образуют "замороженный" остов.)

Обычно утверждают, что понятие спаривания для молекул В₂,O₂ и т. п. вообще теряет смысл и парамагнетизм этихмолекул может быть адекватно объяснен только в рамках метода МО. Но это утверждение справедливо лишь отчасти. Действительно, как уже отмечалось, спаривание спиновых моментов в таких молекулах не осуществляется или осуществляется не в полной мере. Однако мы можем говорить о спаривании орбитальных моментов λ. Согласно методу МО для я-электронной системы (λ = 1) можно построить две МО, π₊ и π_-, соответствующие двум возможным проекциям момента λ = ±1 на ось молекулы, а из них двухэлектронную функцию-детерминант

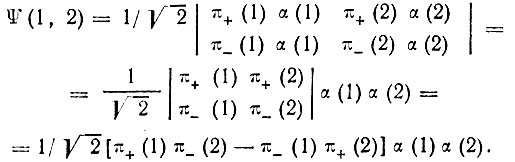
Здесь выражение в квадратных скобках совершенно аналогично выражению для двухэлектронной спиновой функции (спин-инварианта): Таким образом, наряду с понятием спин-валентности V^(S) вводится эквивалентное ему понятие орбитальной валентности V^(l). Формулы (3.11) и (3.12) остаются справедливыми и для V^(l). Например, для молекулы В₂:

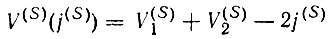)(3.14)

и

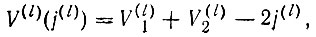(3.15)

а также

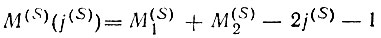(3.16)

и

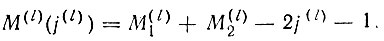(3.17)

где

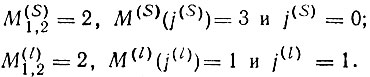
Следует подчеркнуть, что как спиновая, так и орбитальная валентность характеризуют состояние атома в молекуле. Их значения определяются не только природой данного атома, но и тем, с какими атомами он связан в молекуле. Так, спин-валентность бора в В₂ равна нулю (V^(S) = 0), и связь образуется за счет единичной орбитальной валентности (V^(l) = 1). В молекуле ВН, наоборот, реализуется единичная спин-валентность и нулевая орбитальная валентность. Свободный атом бора характеризуется нулевыми значениями и той, и другой валентностей.

Рассмотрение молекулы O₂ аналогично приведенному выше и отличается от него лишь учетом σ-связи 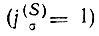и формальной заменой π-электронов на "дырки" в π-электронной оболочке. При этом полная валентность V = V^(S) + V^(l) = 1 + 1 = 2 и полная кратность связи j = j^(S) + j^(l) = 1 + 1 = 2.

К сожалению, идея орбитальной валентности не получила широкого распространения и была забыта. Это, на наш взгляд, объясняется тем, что химия триплетных состояний и свободных радикалов получила значительное развитие лишь в последние годы. Однако описание электронной структуры таких, в большинстве своем нестабильных, частиц проводится в настоящее время в терминах метода МО.

Обратимся теперь к некоторым математическим аспектам рассмотренных выше работ. Их авторы одни из первых осознали ту важную роль, которую играет теория групп перестановок в анализе электронной структуры молекул как систем тождественных частиц. Выражение свойств симметрии волновой функции с помощью теории групп перестановок позволяет построить так называемую "бесспиновую" схему квантовой химии, получившую развитие в работах И. Г. Каплана [14], Матсена [69] и др. Однако это потребовало более детального исследования перестановочной симметрии координатных волновых функций, соответствующих состоянию с заданным полным спином, которая обеспечивает в соответствии с принципом Паули антисимметричность полной многоэлектронной функции относительно перестановки пространственных координат и спиновых переменных двух электронов. Решающий шаг в этом направлении был сделан лишь в 1940 г. В. А. Фоком [26]. Если же говорить о работах Гайтлера и Лондона конца 20-х годов, то, как заметил Ван Флек, "формулировка математической секулярной проблемы, связанная со спариванием спинов... была скорее курьезом ранней истории". Очевидно, этот "курьез" явился следствием того, что развитие альтернативного (бесспинового) подхода натолкнулось на существенные трудности. Действительно, правильные (с точки зрения перестановочной симметрии, точнее, принципа Паули) координатные волновые функции получены не были, что и привело к переоценке роли спинового спаривания^*. Впоследствии, когда такие функции удалось получить, доминирующее положение в квантовой химии уже занимал детерминантный метод Слэтера (см. гл. 2), разработанный им в теории многоэлектронных атомов и распространенный затем Борном на молекулы. Успешное применение метода Слэтера, позволяющего при определении многоэлектронных волновых функций обойтись без использования теории групп, привело к постепенному исчезновению "перестановочно-групповой чумы". В свете сказанного, утверждение, что основы "бесспиновой" квантовой химии были заложены в конце 20-х годов (например, [69]), следует принимать с указанными выше оговорками.

^* (Этому, по мнению Ван Флека, способствовало еще и то, что выражение для оператора обменной энергии, как показал Дирак, можно записать в виде V_ij = -¹/₂*(1+4S_iS_j)A_ij. Однако такая запись является формальной и не связана с какими-либо действительными электронными спин-спиновыми взаимодействиями, приводящими к образованию химической связи.)

В 30-х годах круг исследователей, занимающихся проблемами квантовой химии, несколько расширился - появились работы Румера, Вейля, Борна, Теллера и др. В результате была разработана общая теория возмущений по межэлектронному взаимодействию, при этом также широко использовалась теория групп перестановок (метод Гайтлера-Лондона-Румера-Вейля). В основе теории геттингенских авторов лежали следующие рассуждения.

Многоатомная молекула рассматривалась ими как единая многоэлектронная система. Состояния электронов в отдельных атомах (А, В, С ...) описывались одноэлектронными функциями φ_i^A(r), φ_j^B(r) и т. п. Многоэлектронную функцию системы при отсутствии взаимодействия между атомами можно представить в виде произведения этих одноэлектронных функций:

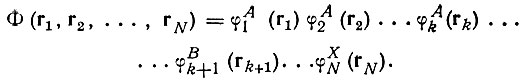(3.18)

Ввиду неразличимости электронов, помимо функции (3.18), можно написать еще ряд функций, полученных из нее перестановкой координат электронов. Всего, таким образом, мы получим ЛМ функций. При учете взаимодействия между атомами все эти функции можно использовать в качестве нулевого приближения в теории возмущений. Многоэлектронные функции молекулы должны представляться их линейными комбинациями, коэффициенты которых определяются секулярными уравнениями порядка N\. Так как для систем, представляющих химический интерес, порядок соответствующих секулярных уравнений становится чрезвычайно большим, необходимо использовать любую возможность для его уменьшения путем деления рассматриваемой секулярной задачи на более простые. Как было показано работами Гайтлера, Румера и Вейля, эта задача может быть решена в значительной степени с учетом перестановочной симметрии и принципа Паули. При этом разрабатывался математический аппарат, соответствующий теории спин-валентности. Для большинства молекул в их основных состояниях полный спиновый момент имеет нулевое значение. Учитывая, что операторы спинового момента действуют на спиновые переменные отдельных электронов, а не на их пространственные координаты, можно представить многоэлектронные функции в виде произведения двух сомножителей, один из которых зависит только от пространственных, а другой только от спиновых переменных. Последний может быть построен из одноэлектронных спиновых функций а и р, удовлетворяющих уравнениям

(3.19)

где 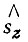- оператор проекции одноэлектронного спинового момента на ось квантования z. Так, например, для молекулы водорода, включающей два электрона, как было показано Гайтлером и Лондоном, можно построить четыре двухэлектронные спиновые функции:

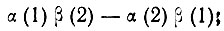(3.20)

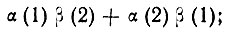(3.21)

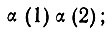(3.22)

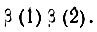(3.23)

Только первая из этих функций соответствует синглетному состоянию и инвариантна по отношению к повороту осей квантования, так как при любом их выборе проекция нулевого спинового момента равна нулю. Поэтому эта функция, обозначаемая как [β], была названа Вейлем спин-инвариантом.

При рассмотрении более общего случая молекул с любым четным числом электронов многоэлектронная спиновая функция χ(σ₁,...,σ_N) строилась в виде произведения таких спин-инвариантов. Как и в случае построения функций Ф(r₁,..., r_N), в силу неразличимости электронов можно построить множество функций (многоэлектронных спин-инвариантов) χ(σ₁,...,σ_N), отличающихся перестановкой электронов или так называемой схемой спинового спаривания. Эти функции, как правило, образуют линейно-зависимый набор, т. е. некоторые из них являются линейными комбинациями остальных и должны быть исключены из рассмотрения. Формула, определяющая число линейно-независимых функций, была получена Румером [76]. Им же было предложено графическое правило, позволяющее выявить и устранить линейные зависимости между функциями, полученными путем спинового спаривания. Согласно правилу Румера, каждой одноэлектронной спиновой функции следует сопоставить точку на плоскости, расположив точки таким образом, чтобы они лежали на окружности или на другой выпуклой кривой. Затем эти точки соединяются друг с другом штрихами, каждый из которых является графическим представлением определенного простейшего спин-инварианта. Как показал Румер, многоэлектронные функции, соответствующие диаграммам с непересекающимися штрихами, линейно независимы, а остальные содержащие, по крайней мере, одно пересечение, являются, их линейными комбинациями.

В качестве примера можно привести шестиэлектронную систему. В этом случае можно составить пять диаграмм Румера с непересекающимися штрихами (рис. 13, а). Им соответствуют следующие спин-инварианты:

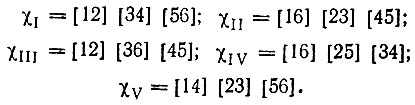(3.24)

Функция 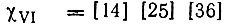(рис. 13,б) будет представлять собой линейную комбинацию функций (3.24):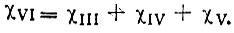

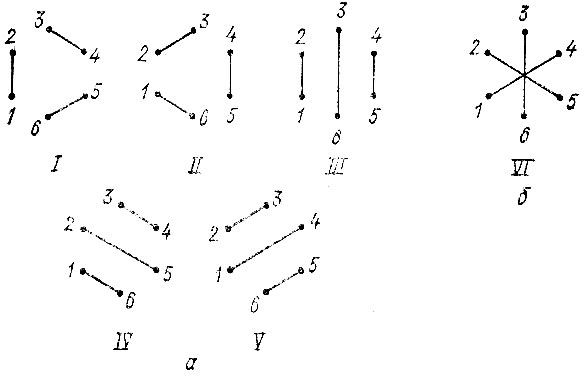
Рис. 13. Диаграммы Румера: а - с непересекающимися и б - с пересекающимися штрихами для молекулы бензола

К сожалению, правило Румера применимо лишь в том случае, когда число электронов не слишком велико. Если учитывать электроны атомов, образующих молекулу, то оно оказывается практически неприемлемым^*. Но иногда в рассмотрение включается лишь часть электронов. Например, при изучении плоских органических молекул часто ограничиваются учетом только одной π-орбитали от каждого атома. Именно в этом случае правило Румера нашло применение.

^* (Позднее, в 1937 г., была сформулирована более общая методика построения линейно-зависимых наборов спиновых функций с использованием таблиц Юнга.)

В литературе иногда обращают внимание на аналогию между классическими структурными формулами и диаграммами Румера. Однако при этом нельзя упускать из виду того, что между ними имеются существенные различия. Структурные формулы характеризуют связи различной кратности между атомами, что изображается соответствующим числом валентных штрихов. В диаграммах Румера штрихи характеризуют связи отдельных орбиталей (возможно, но не обязательно, атомных). Поэтому чтобы изобразить диаграмму Румера для бензола, мы должны соединить штрихами 30 точек (для π-электронной подсистемы бензола только 6 точек).

Классические структурные формулы определяют индивидуальные химические соединения, характеризуемые индивидуальными геометрическими свойствами и распределением валентностей атомов по химическим связям. При этом вещества, отвечающие разным структурным формулам, обладают разными ядерными конфигурациями, т. е. различным расположением атомов в пространстве. Диаграммы Румера определяют базис для описания состояний электронной системы соединения при фиксированной и одинаковой для всех диаграмм ядерной конфигурации, т. е. все диаграммы соответствуют одномуитому же химическому соединению.

Теперь следует подробнее сказать о том, как в методе Гайтлера-Лондона-Румера-Вейля (ГЛРВ) учитывался принцип антисимметрии. Согласно принципу Паули, функция Ψ, описывающая состояние многоэлектронной системы, должна быть антисимметрична относительно перестановки пространственных и спиновых переменных любых двух электронов и обращаться в нуль, если эти переменные совпадают. Это достигается действием иператора антисимметризации

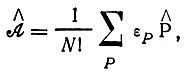(3.25)

где 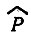- оператор перестановок пространственных и спиновых переменных; ε_P = +1 для четных перестановок и (-1) - для нечетных. В результате получаем функцию

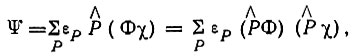(3.26)

удовлетворяющую необходимому условию антисимметричности.

По методу ГЛРВ в нулевом приближении теории возмущений можно считать справедливым равенство

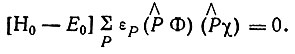(3.27)

Уравнения, соответствующие первому приближению теории возмущений, получаются умножением равенства (3.27) слева на функции 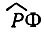и интегрированием получаемых выражений по всем переменным, кроме спиновых.

Гамильтониан 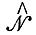системы можно представить в виде суммы

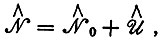(3.28)

где 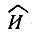- оператор возмущения, включающий межэлектронные взаимодействия, отсюда

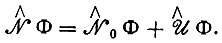(3.29)

Уравнения первого порядка теории возмущений приводятся к виду

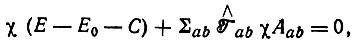(3.30)

где 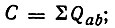; Q_ab - кулоновский и А_аb - обменный интегралы; 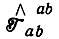- оператор транспозиции орбиталей а и b; Е - Е₀ - поправка первого порядка к полной энергии системы. Если интегралы Q и A известны, то уравнение (3.30) позволяет определять энергию многоатомной системы, судить о прочности химических связей в ней и их свойствах.

К середине 30-х годов число работ, посвященных математическим аспектам многоэлектронной проблемы, постепенно уменьшается, и уже примерно с 1935 г. подобные исследования не проводятся. Это привело, в свою очередь, к тому, что развитие метода ВС в последующие десятилетия было сильно заторможено. Причины прекращения попыток создания на основе метода ВС строгой неэмпирической теории многоэлектронных систем, по нашему мнению, состоят в следующем:

во-первых, теория была слишком сложной и громоздкой для ее численной реализации, тем более, что достаточно мощной вычислительной техники в то время еще не было;

во-вторых, метод ГЛРВ практически исчерпал свои возможности для развития качественной интерпретации природы химической связи;

в-третьих, некоторые ученые (Гайтлер, Лондон, Теллер) начали работать в других областях физики, отойдя от квантово-химических проблем;

в-четвертых, не следует забывать также о драматических событиях в немецкой науке (распад научных школ, эмиграция ученых и т. п.), которые связаны с приходом к власти фашистов.

Все это вместе взятое привело к тому, что ведущее место в квантовой химии (речь идет о методе ВС!) заняли работы представителей американской школы и прежде всего исследования Полинга. Однако многие результаты, полученные немецкими теоретиками, легли затем в основу современного формализма метода ВС.