Обобщенный формализм метода ВС как реализация идей Гайтлераг Лондона, Румера и Вейля

Обратимся теперь к рассмотрению метода ВС в его современной формулировке. При этом мы будем пользоваться некоторыми понятиями и концепциями, анализ исторического развития которых будет дан ниже. В этом отношении изложение будет иметь отчасти ретроспективный характер, что позволит нам, с одной стороны, четче выявить основное позитивное содержание работ Гайтлера, Лондона, Румера, Вейля и других авторов, а с другой - установить связь между рассмотренной выше формальной химико-алгебраической аналогией и основными понятиями теории спин-валентности, т. е. связать с ней ее "математическую предысторию". Наиболее важным, однако, является то, что в свете излагаемой здесь общей теории станет более ясной взаимосвязь обсуждаемых концепций гибридизации и резонанса, которые исторически возникли независимо друг от друга. А это, в свою очередь, позволит лучше понять внутреннюю логику развития квантовой химии.

Как мы видели выше, основная идея метода ВС заключается в предположении, что атомы или, точнее, атомные орбитали при образовании молекулы в значительной степени сохраняют свою индивидуальность. Из орбиталей отдельных атомов A, Б, ..., находящихся на конечном расстоянии друг от друга, но условно считающихся невзаимодействующими, строится многоэлектронная бесспиновая функция-произведение

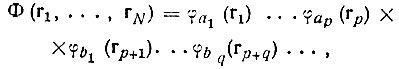(3.31)

где 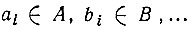и т. п. При этом φ_а1,...,φ_аp могут быть (в общем случае) не сферическими орбиталями изолированного атома, а их линейными комбинациями, т. е. гибридными атомными орбиталями.

Совокупность всех орбиталей ф называется в методе ВС конфигурацией, а каждый из наборов (φ_а1,...,φ_аp)- валентной конфигурацией Г_A атома A. Некоторые из атомных орбиталей входят в Г_А дважды (т. е. φ_аi = φ_аj) и называются спаренными. Число неспаренных орбиталей в конфигурации Г_А называется спин-валентностью атома A, находящегося в соответствующем валентном состоянии. Это определение спин-валентности является обобщением, данным Лондоном. Действительно, если пренебречь гибридизацией атомных орбиталей, то оба определения станут идентичными, т. е. спин-валентность окажется равной мультиплетности основного (низшего) терма, уменьшенной на единицу.

Функция Φ домножается на функцию Θ(σ₁,...,σ_N), зависящую от спиновых переменных всех электронов. Многоэлектронная функция Ψ, определяющая электронное состояние молекулы, должна быть собственной для оператора квадрата полного спинового момента 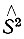N-электронной системы, которую представляет молекула. Так как 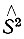действует только на функцию Θ указанное условиt накладывает определенные ограничения только на Θ, но не на Φ.

Подавляющее число веществ, способных к длительному существованию, состоит из молекул с нулевым полным спином, т. е. находится в синглетном состоянии. Для простоты изложения в дальнейшем будут рассматриваться только такие молекулы.

Каждой атомной орбитали φ соответствует одна из двух одноэлектронных спиновых функций α(σ) и β(σ), которые являются собственными для одноэлектронного оператора проекции спинового момента на ось квантования [см. (3. 19)].

Функция Θ может быть построена из одноэлектронных спиновых функций следующим образом:

• из пары функций α(σ) и β(σ) составляется двухэлектронная функция
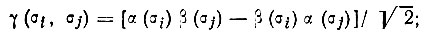  (3.32)
  
• перемножением ^N/₂ функций γ, зависящих от спиновых переменных различных электронов, получается функция
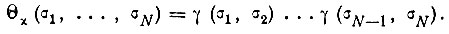  (3.33)
  

Необходимость индексации функции Θ обусловлена неоднозначностью ее построения из функций γ.

Если конфигурация N-электронной системы содержит п неспаренных АО, то, как это было показано Гайтлером и Румером [51-52], можно построить 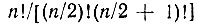линейно-независимых Θ_χ. Например, для π-электронной системы бензола, включающей шесть электронов и столько же атомных π-орбиталей, можно построить пять независимых Θ_χ (χ = 1,...,5).

Таким образом, оказывается необходимым рассмотрение функции вида

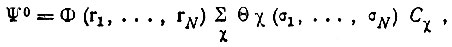(3.34)

содержащей числовые коэффициенты С_χ, которые должны определяться минимизацией полной электронной энергии молекулы.

Согласно принципу Паули, функция состояния многоэлектронной системы должна быть антисимметричной относительно всевозможных перестановок (r_iσ_i) → (r_j, σ_j). Функция Ψ⁰, однако, такой не является, и поэтому ее следует антисимметризовать. Учитывая, что Ф является произведением орбиталей φ, легко видеть, что процедура антисимметризации сохраняет соответствие между парой орбиталей {φ_i, φ_j} и некоторой двух-электронной спиновой функцией у для каждого слагаемого в сумме (3.34), характеризующегося некоторым индексом χ и называемого структурой ВС. Можно сказать поэтому, что орбитали φ_i и φ_j в некоторой структуре ае спарены. Таким образом, одно из центральных понятий ранних квантовохимических работ - понятие спаривания электронов (точнее, атомных орбиталей) - сохраняется и в более общей теории при правильном учете принципа антисимметрии.

Если каждой орбитали φ_i сопоставить точку на плоскости, то спаривание двух орбиталей можно представить графически отрезком, соединяющим две соответствующие точки. Так, например, одна из структур молекулы аммиака NH₃ может быть представлена диаграммой I (рис. 14). Здесь прерывистой линией обведена группа точек, соответствующих орбиталям атома азота. Стягивая каждую из таких групп в одну точку, можно получить диаграмму II связей атомов в структуре ВС. Аналогично для молекулы азота N₂ получаем диаграмму III.

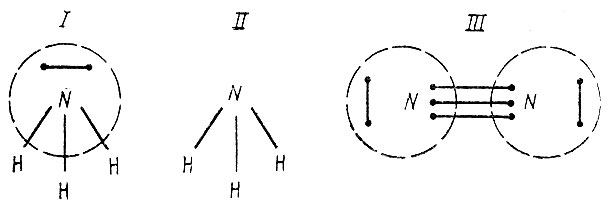
Рис. 14. Диаграммы связей атомов в молекулах NH₃ и N₂

Иногда возможно с достаточной степенью точности представить электронное строение молекулы одной структурой (приближение идеального спаривания). Тогда кратность связи атомов отождествляется с числом штрихов, соединяющих соответствующие этим атомам группы точек на диаграмме связей, а сами диаграммы вида II становятся идентичными химическим структурным формулам.

В других случаях необходимо учитывать несколько структур . Например, для молекулы бензола следует принимать во внимание по крайней мере две структуры Кекуле. В таких "неклассических" случаях значения кратностей связей должны, очевидно, усредняться по структурам с учетом веса (ω_χ) каждой структуры χ в разложении полной многоэлектронной функции Ψ:

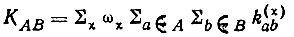(3.35)

где 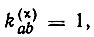если атомные орбитали аиЬ спарены в структуре χ; 0 - в противном случае;

А и В обозначают атомы и с оответствующие им наборы атомных орбиталей.

Вес структур зависит, вообще говоря, как от коэффициентов С_χ , так и от перекрывания соответствующих многоэлектронных функций. Вследствие неортогональности последних понятие веса не является ни простым, ни однозначным. Удовлетворительное определение этого понятия, к сожалению, до сих пор отсутствует. Однако в ряде случаев вес структур определяется исключительно из соображений симметрии. Для π-электронной системы бензола, например, вес двух кекулевских структур (рис. 15) одинаков, так как эти структуры эквивалентны по симметрии. Поэтому если пренебречь прочими структурами, то ω_χ = 0,5 (χ = 1,2), и с учетом σ-системы, описываемой в приближении идеального спаривания единственной структурой, кратность связи двух соседних атомов углерода равна

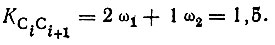(3.36)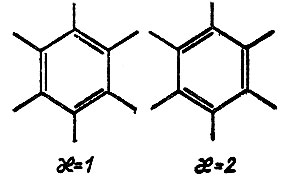

Рис. 15. Кекулевские структуры молекулы бензола

Аналогично для соседних атомов углерода и водорода

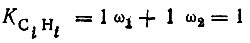(3.37)

(см. рис. 15).

Проблему более серьезную, чем определение веса отдельной структуры, представляет неоднозначность выбора самих структур. Так, для π-электронной системы бензола линейно-независимый базис может включать пять структур, характеризуемых диаграммами I-V (рис. 16)^*.

^* (Этим диаграммам соответствуют стандартные таблицы Юнга:)

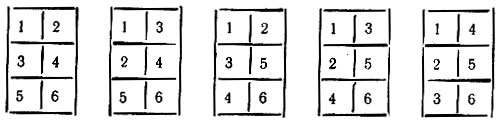
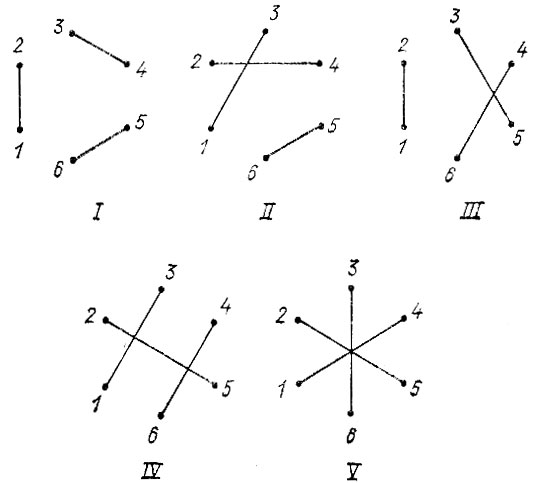
Рис. 16. Линейно-независимые структуры молекулы бензола, отвечающие стандартным таблицам Юнга

Очевидно, что каким бы ни был вес этих структур, π-электронные составляющие кратностей связей С₂С₃, С₄С₅ и C₁C₆ равны нулю, и, следовательно, эти связи, в отличие от связей С₁C₂, С₃С₄ и C₅С₆, оказываются одинарными. Значения кратностей для остальных связей также не согласуются с симметрией молекулы бензола. Набор структур Кекуле и Дьюара для бензола позволяет получить разумные значения кратностей связей. Однако в общем случае сформулированная проблема пока не решена.

Валентность атома А можно определить как сумму кратностей связей, образуемых атомом А:

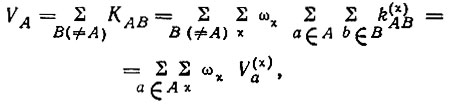(3.38)

где 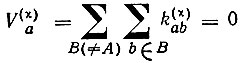или 1 - вклад атомной орбитали 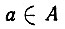в валентность атома А.

В рамках метода ВС с использованием единственной для каждого атома А валентной конфигурации Г_А (без учета ионных структур) для синглетных состояний V^(χ)_a в действительности не зависит от χ. Учитывая это обстоятельство, а также то, что вес всех структур в сумме равен единице, валентность атома можно представить в виде суммы

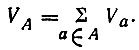(3.39)

В соответствии с последним равенством валентность атома А оказывается равной числу неспаренных орбиталей в валентной конфигурации Г_А этого атома, т. е. его спин-валентности, и не зависит, следовательно, ни от выбора линейно-независимого набора структур, ни от используемого способа определения веса отдельной структуры.

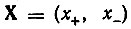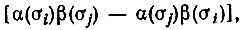Возвращаясь к рассмотренной ранее формальной "химико-алгебраической аналогии", можно сказать, что ее физический смысл был вскрыт в методе валентных связей. Оказалось, что двухкомпонентному вектору соответствует пара одноэлектронных спиновых функций α(σ) и β(σ), одночленному инварианту соответствует двухэлектронная спиновая функция которая на заре квантовой химии называлась спин-инвариантом. Кроме того, произведению одночленных инвариантов в соответствующих степенях отвечает понятие структуры в методе ВС, а валентности как показателю степени V_X , в которой X входит в F(X, Y,...), - число неспаренных орбиталей в валентной конфигурации Г_X.