Анализ заселенности атомных орбиталей

[23]

В квантовой химии функции Ψ, описывающие состояния многоэлектронных систем, обычно выражаются через АО или подобные им более элементарные функции, центрированные на различных ядрах молекулы. Такой выбор одноэлектронного базиса {φ} основан на предположении, что атом, представленный определенным набором орбиталей в таком базисе, сохраняет в молекуле свою индивидуальность. В связи с этим встает задача построения формализма, позволяющего характеризовать состояния химически связанных атомов и установить корреляции между этими состояниями и состояниями невзаимодействующих атомов.

Анализ заселенностей орбиталей, представляющих атом в молекуле, в значительной степени определяет его валентное состояние и является Эффективным средством исследования природы химической связи, ее анатомии, аддитивности и трансферабельности связанных с атомами молекулярных свойств или их зависимости от окружения рассматриваемого атома в различных соединениях. Анализ заселенностей АО позволяет осуществить выбор базисных функций, соответствующих валентным состояниям атомов, и необходим при расчете электронной структуры молекул и кристаллов полуэмпирическими методами с самосогласованием по формальным зарядам и валентным конфигурациям

атомов. Однако анализ заселенностей осложняется перекрыванием атомных орбиталей в молекуле.

Если последние ортогональны, т. е. не перекрываются, то их заселенности определяются однозначно. При этом заселенность па имеет смысл вероятности нахождения электрона в состоянии, заданном атомной орбиталью φ_а, и может быть выражена как математическое ожидание:

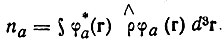(4.58)

Если атомные орбитали неортогональны, то положение осложняется. Понятие заселенности отдельной АО становится неоднозначным и распадается на дополняющие друг друга понятия полной, неподеленной и аддитивной заселенности и заселенности перекрывания, которые связаны с различными способами ортонормировки атомно-орбитального базиса {φ}.

Полные заселенности (n⁺_а) орбиталей φ_а неортогонального базиса {φ} определяются аналогично заселенностям ортогонального базиса:

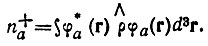(4.59)

Предполагая, что оператор электронной плотности ρ представлен в базисе {φ} матрицей 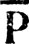, определение (4.59) можно переписать также в виде

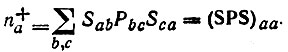(4.60)

Детальное исследование заселенностей n⁺_a было проведено Дэвидсоном [37] и Роби [74], которые показали, в частности, что

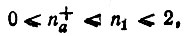
где n₁ - наибольшая из естественных заселенностей. Это неравенство, как и аналогичные неравенства для определяемых ниже заселенностей n^-_a и n⁰_а, следует из условия антисимметрии многоэлектронной функции Ψ(х₁,..., х_N) относительно перестановок электронных координат.

Неподеленную заселенность (n^-_а) орбитали φ_а можно определить как заселенность ее компоненты, которая ортогональна ко всем прочим орбиталям φ:

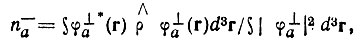(4.62)

где

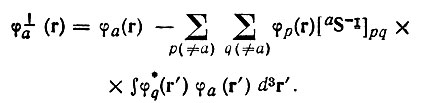(4.63)

^aS в формуле (4.63) обозначает матрицу перекрывания, полученную из полной матрицы S вычеркиванием интегралов перекрывания S_ab, включающих рассматриваемую орбиталь φ_а.Такая ортогонализация (аналогичная ортогонализации по методу Шмидта) исключает из полной заселенности n⁺_а ту ее часть, которая принадлежит не только φ_а, но и остальным орбиталям неортогонального базиса (рис. 23).

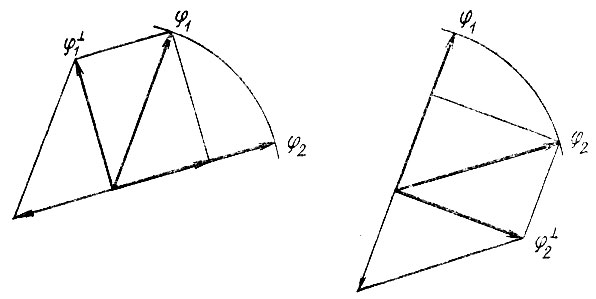
Рис. 23. Геометрическая иллюстрация к определению неподеленной электронной заселенности

Учитывая отмеченное Галлупом и Норбеком [40] равенство

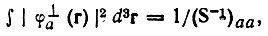(4.64)

выражение(4.62) можно привести к чрезвычайно простому виду

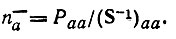(4.65)

В частном случае одноэлектронной системы, состояние которой описывается орбиталью

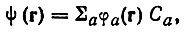(4.66)

диагональные элементы матрицы плотности равны

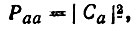(4.67)

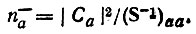(4.68)

Эта формула, то чиее ее правая часть, приводилась в работе [40], но лишь в качестве промежуточного результата. Окончательное выражение для заселенностей (по Галлупу и Норбеку) получалось путем нормирования n^-_а на единицу:

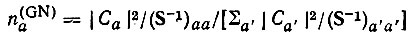(4.69)

Обобщение формулы (4.69) на многоэлектронные системы, очевидно, должно осуществляться заменой |С_а|² на Р_аа:

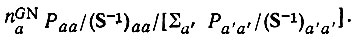(4.70)

Однако такой подход к проблеме является ошибочным. Расчеты свидетельствуют, в частности, о чрезмерно больших значениях n(GN) для АО внутренних оболочек и неподеленных электронных пар. Например, в молекуле LiH:

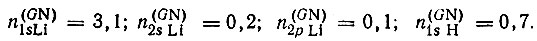
Заселенность перекрывания орбитали φ_а с остальными орбиталями неортогонального базиса φ определяется как разность между полной и неподеленной заселенностями:

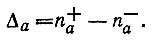(4.71)

Заселенность перекрывания 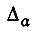представляет ту долю полной электронной заселенности, которая принадлежит одновременно к рассматриваемой и всем прочим базисным АО. Нетрудно убедиться в том, что величина 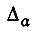равна нулю, если АО φ_а не перекрывается ни с одной из орбиталей базиса φ, т. е. если

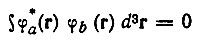(4.72)

для всех b≠a.

Аддитивная заселенность.

Сумма засел енностей n⁺_a или n^-_а по всем базисным орбиталям совпадает с числом электронов (N) в рассматриваемой системе только в том случае, если эти орбитали ортогональны. Иными словами, заселенности орбиталей неортогонального базиса неаддитивны.

Чтобы определить аддитивные заселенности АО, необходимые, например, для вычисления формальных зарядов атомов, следует сопоставить каждой АО φ_а неортогонального базиса орбиталь φ^λ_a некоторого ортонормированного базиса. Требование минимальной деформации исходных орбиталей в процессе ортогонализации однозначно отбирает из всех возможных методов ортогонализации "симметричный" метод Лёвдина (рис. 24)

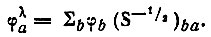(4.73)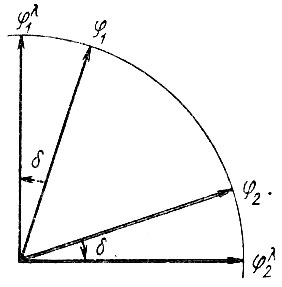

Рис. 24. Геометрическая иллюстрация лёвдинской ортогонализации двух неортогональных векторов φ₁ и φ₂

Как показали Слэтер и Костер, ортонормировка по Лёвдину сохраняет трансформационные свойства неортогонального базиса в том смысле, что при унитарном преобразовании базиса {φ} соответствующий лёвдинский базис {φ^λ} преобразуется той же унитарной матрицей. Отсюда следует, в частности, что орбитали φ^λ_а исходного многоцентрового базиса АО и соответствующие им орбитали φ^λ_a преобразуются по одним и тем же представлениям подгруппы G_A точечной группы симметрии молекулы (G). При этом подгруппа G_A включает только те преобразования группы G, которые не затрагивают центр А (т, е, ядро атома A). Таким образом, орбитали φ_a и ф^λ_a обладают одинаковыми свойствами симметрии относительно указанных преобразований.

Согласно теореме Карлсона и Келлера, лёвдинский базис 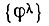отличается от всех прочих базисов, полученных ортогонализацией исходного базиса {φ}, максимальной близостью к {φ} в смысле минимума среднеквадратического отклонения

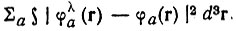(4.74)

Представление об изменении формы и размеров атомных орбиталей при их ортогонализации можно получить, сравнивая средние значения и и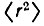ли среднеквадратические радиусы 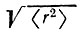Для сферических АО с соответствующими значениями для ортогонализованных орбиталей. Такие вычисления (в табл. 8 приведены результаты для молекулы N₂) свидетельствуют, что орбитали лёвдинского базиса, соответствующие валентным АО, могут быть локализованными в окрестности атомных ядер в большей степени, чем исходные. Сжатие орбиталей наблюдается как в "поперечном", так и в "продольном" направлениях. 1s-Орбитали внутренних оболочек при ортогонализации несколько расширяются, оставаясь тем не менее существенно локализованными у своих ядер. Среднеквадратический радиус этих орбиталей в несколько раз меньше, чем валентных.

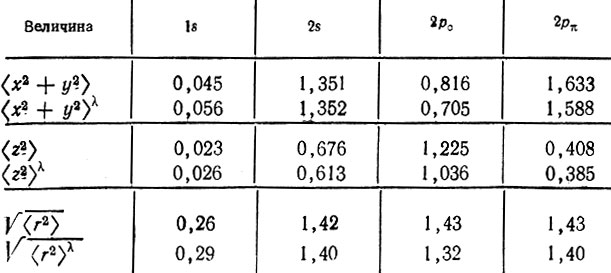
Таблица 8. Средние значения 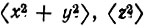и среднеквадратические радиусы 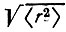характеризующие АО азота и соответствующие лёвдинские орбитали в молекуле N₂

С учетом сказанного выше, аддитивные (лёвдинские) заселенности (n⁰) орбиталей неортогонального базиса φ следует отождествлять с заселенностями соответствующего лёвдинского базиса:

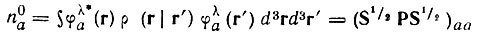(4.75)

Формальный заряд q_A атома А определяется зарядом его ядра Z_A и аддитивными заселенностями представляющих этот атом орбиталей:

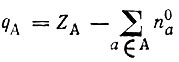(4.76)div> формальные заряды атомов отражают перераспределение электронной плотности при образовании молекулы и являются полезной характеристикой валентного состояния атома. В частности,они позволяют производить интерполяцию атомных свойств по известным свойствам свободных атомов. Так, потенциалы ионизации химически связанных атомов могут оцениваться по формуле

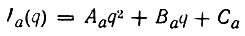(4.77)

Следует отметить сильную зависимость потенциала ионизации Вот заряда атома. Несколько примеров, характеризующих эту зависимость, приведено в табл. 9.

Таблица 9. Зависимость орбитальных потенциалов ионизации от атомного заряда q (экспериментальные данные) [27]

Формальные заряды атомов используются часто для оценки энергии электростатического взаимодействия

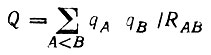(4.78)

и для определения дипольных моментов больших молекул в точечном приближении

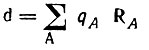(4.79)

Рассмотрим теперь несколько примеров, иллюстрирующих вложенный формализм анализа заселенностей многоцентрового азиса перекрывающихся АО.

1. Для молекулы Н₂ для π-электронных оболочек молекул азота (N₂), этилена, ацетилена и для ряда других аналогичных двухорбитальных систем, содержащих по два электрона, матрица плотности и заселенности АО определяются симметрией и перекрыванием базисных АО:

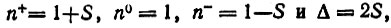
где интеграл перекрывания АО S>0. Уменьшая расстояние между атомами, в пределе мы получим

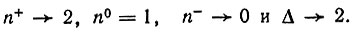
Напротив, при бесконечном разведении атомов

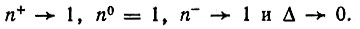
2. π-Электронные системы в молекулах F₂, ClF и в других аналогичных молекулах независимо от их симметрии (D_∞h или C_∞h) характеризуются заселенностями АО π-типа

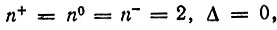
которые не зависят от интегралов перекрывания. Эти АО представляют неподеленные электронные пары соответствующих атомов.

3. Валентное состояние атома Li в молекуле LiH (табл. 10) характеризуется положительным формальным зарядом и существенным перераспределением электронной плотности между 2s-орбиталью и виртуальной (для основной конфигурации свободного атома Li) 2pσ-орбиталью. Две эти АО незначительно различаются по заселенности перекрывания в молекуле LiH, в то время как 1s-AO лития практически не участвует в образовании химической связи и представляет неподеленную электронную пару атомного остова.

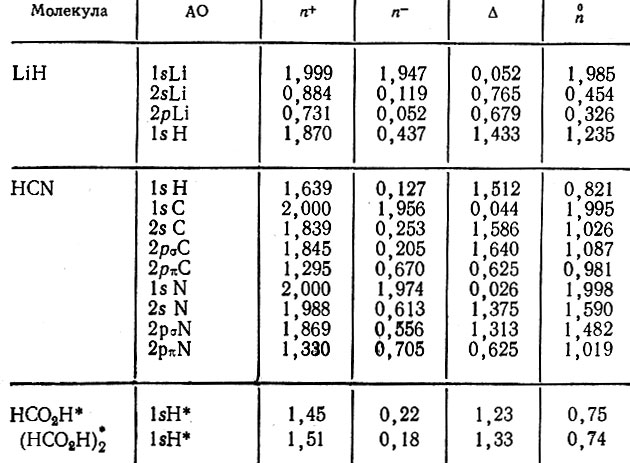
Таблица 10. Анализ заселенностей АО в молекулах LiH, HCN, НСO₂Н, (НСO₂Н)₂

4. Анализ заселенностей АО в молекуле HCN (см. табл. 10) свидетельствует о том, что АО π-типа характеризуется существенно меньшими по сравнению с АО σ-типа значениями заселенностей перекрывания. Малые значения формальных атомных зарядов в HCN указывают на ковалентный характер химической связи в этой молекуле.

5. Анализ заселенностей атомов водорода, ответственных за образование водородной связи, в молекулах муравьиной кислоты и ее димера (см. табл. 10), осуществленный на основе расчета матрицы плотности расширенным методом Хюккеля с самосогласованием по формальным зарядам атомов, показывает, что водородная связь обусловливает заметное изменение электронных заселенностей мостикового атома водорода (Н^*). При этом заселенность перекрывания существенно возрастает вследствие увеличения полной и уменьшения неподеленной заселенностей. В то же время аддитивная заселенность и соответствующий ей формальный заряд атома водорода почти не изменяются.

Анализ заселенностей по Малликену. Наряду с изложенным выше подходом к анализу заселенностей существуют альтернативные подходы к этой проблеме. Наиболее популярными до настоящего времени являются предложенные Малликеном [67] определения нетто-заселенности Р_аа, заселенности перекрывания

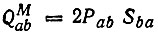(4.80)

и полной зеселенности

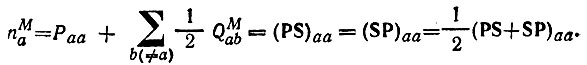(4.81)

В основе этих определений фактически лежит равенство

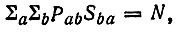(4.82)

представляющее условие нормировки матрицы плотности на число электронов (N) в молекуле. Левую часть этого равенства можно записать в виде суммы членов, относящихся к отдельным АО и их парам:

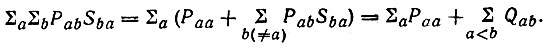(4.83)

Таким образом, сумма нетто-заселен ноет ей всех АО и всех заселенностей перекрывания оказывается равной числу электронов в системе.

Однако это нельзя рассматривать как обоснование анализа заселенностей по Малликену ввиду неоднозначности разложения вида

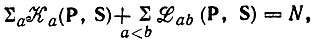(4.84)

где слагаемые 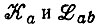выражены через элементы матрицы плотности Р_аb и интегралы перекрывания S_ab.

Серьезным аргументом против предложенного Малликеном анализа заселенностей является то, что нетто- и полные заселенности могут принимать значения Р_aa>2 и n^M_a>2. Не меньшую трудность представляет интерпретация отрицательных значений Q^M_ab, имеющих смысл отрицательного числа электронов, приходящихся на связь АО φ_a и φ_b.

Анализ заселенностей по Христоферзену и Бэкеру [33] формулируется в терминах коэффициентов разложения МО ψ_i по базисным АО φ_a:

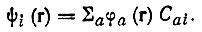(4.85)

При этом предполагается, что вес (или заселенность) АО φ_a, входящей в состав МО ψ_i, пропорционален квадрату модуля соответствующего коэффициента φ_a:

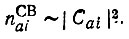(4.86)

Из условия нормировки

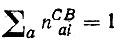(4.87)

для 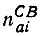получается выражение

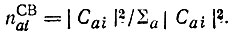(4.88)

Суммированием величин n_ai по всем МО ψ_i с учетом их заселенностей далее определяются величины

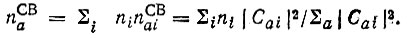(4.89)

Заселенности АО по Христоферзену и Бэкеру, как и заселенности по Малликену, могут принимать значения n^CB_a>2 (табл 11). В связи с этим интересно отметить, что Христоферзен и Бэкер обращали внимание на недопустимость таких значений, когда речь шла о малликеновском анализе заселенностей. Не менее серьезным обстоятельством, компрометирующим определение Христоферзена и Бэкера, является его неинвариантность относительно унитарного преобразования занятых МО, в то время как одноэлектронная матрица плотности и математические ожидания всех физических величин инвариантны относительно такого преобразования.

Таблица 11. Заселенности АО n⁰, n^M и n^CB в двухатомных молекулах LiH, BH, NH, FH, LiF, BF, CO [46]