Индексы химических связей и валентность

В химии принято различать одинарные, двойные, тройные, а также связи дробной кратности между атомами, образующими молекулу. Если МО могут быть локализованы на отдельных атомах и двухцентровых связях, то под кратностью связи двух атомов (А и В) естественно понимать число МО, локализованных на связи АВ. В случае молекул, обладающих неспаренными электронами, т. е. находящихся в основных или возбужденных состояниях с отличной от нуля мультиплетностью по спину, следует говорить о локализации спин-орбиталей и отождествлять с кратностью связи половину числа локализованных на ней молекулярных спин-орбиталей (МСО). В качестве примера можно привести ряд двухатомных гомонуклеарных молекул, для котоых локализованные МО (или МСО) являются либо орбиталями неподеленных электронных пар, либо связывающими двух-центровыми орбиталями (табл. 12).

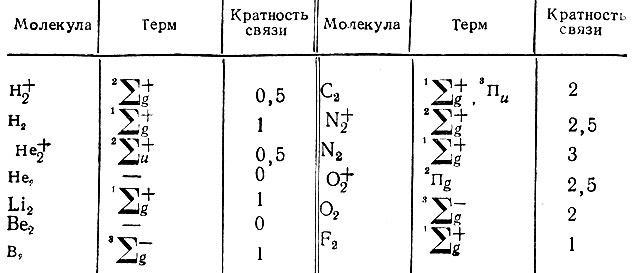
Таблица 12. Кратности связей в некоторых гомонуклеарных молекулах

Однако такой подход к проблеме молекулярно-орбитальной интерпретации понятия кратности химической связи весьма ограничен двумя существенными причинами. Во-первых, локализация МО в орбитали неподеленных электронных пар и двухцентровые связывающие МО, как правило, не является строгой. Во-вторых, локализованные двухцентровые МО могут быть поляризованы, т. е. принадлежать одному из связанных атомов в большей степени, чем другому. При этом исчезает грань между полярной двухцентровой МО и орбиталью неподеленной электронной пары.

Эти причины обусловливают нецелочисленность кратности химических связей в многоатомных молекулах независимо от (того, какой спиновой мультиплетностью характеризуются их состояния. Как частичная делокализация МО, относящихся к некоторой связи, так и их поляризация в направлении любого из связанных атомов должны означать уменьшение кратности этой связи. В то же время делокализация МО, относящихся к другим связям, может вносить определенный вклад в кратность рассматриваемой связи.

Для учета указанных эффектов необходимо квантовохимическое определение кратности химической связи. К настоящему времени в квантовой химии используют довольно много различных индексов, характеризующих химическую связь двух атомов в молекуле, но не все из них соответствуют классическому понятию кратности химической связи. Хотя кратность химической связи не должна быть целочисленной, она должна быть все же величиной неотрицательной (нулевая кратность связи АВ означает отсутствие химической связи между атомами А и В) и инвариантной относительно унитарных преобразований (в частности, поворотов и гибридизации) атомных орбиталей отдельных атомов. Для гомонуклеарных двухатомных молекул квантово-химическое определение кратности должно обеспечивать целые или полуцелые ее значения (см. табл. 12).

Сформулированным условиям удовлетворяет определение кратности химической связи (КА_В) согласно равенству [3]:

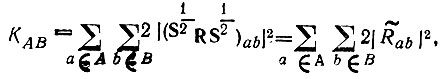(4.90)

где S - матрица перекрывания всех АСО атомов, образующих молекулу; R - матрица, представляющая в базисе этих АСО электронную плотность, точнее ее компоненту, соответствующую максимальному значению проекции полного спинового момента электронов молекулы на ось квантования; а и b - индексы спин-орбиталей атомов А и В.

При отсутствии одноэлектронного спин-орбитального взаимодействия матрица 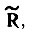, определяемая формулой

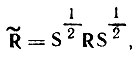(4.91)

имеет квазидиагональный вид

(4.92)

где Р^α и Р^β - одноэлектронные матрицы плотности, соответствующие проекциям спинового момента +¹/₂ и -¹/₂. С учетом последнего равенства К_АВ можно представить в виде

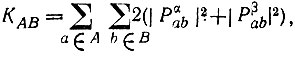(4.93)

а также выразить через матричные элементы электронной (Р) и спиновой (Q) плотности [4]. При этом

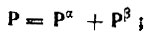(4.94)

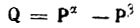(4.95)

и

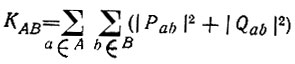(4.96)

Первый член в правой части этой суммы называется индексом Виберга [88] и используется для характеристики химических связей в молекулах с замкнутыми электронными оболочками, если расчет их структуры проводится в рамках приближения нулевого дифференциального перекрывания (S = I) (табл. 13).

Таблица 13. Индексы Виберга для некоторых соединений элементов первых трех периодов периодической системы [30]

Альтернативное квантовохимическое определение кратности химической связи было предложено в работе [42]. Согласно этому определению

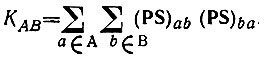(4.97)

В классической теории химической связи каждому атому молекулы сопоставляется определенная валентность, понимаемая как число, характеризующее состояние атома в этой молекуле. Распределение валентности V_A атома A по связям его с остальными атомами молекулы описывается кратностями связей K_AB, причем

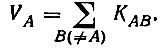(4.98)

Подставляя в это равенство выражение (4.90)$ можно определить V_A через матричные элементы R и S [3]:

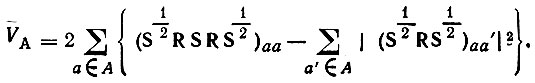(4.99)

В однодетерминантном приближении для молекул, обладающих лишь замкнутыми электронными оболочками, выражение для валентности приводится к виду

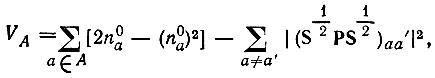(4.100)

где 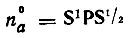- электронная лёвдинская заселенность а-й орбитали, принадлежащей атому А. Последняя сумма может быть исключена из выражения для V_A унитарным преобразованием (гибридизацией) атомных орбиталей [21].

Другое определение валентности

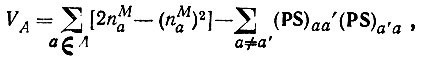(4.101)

где n^M_a - заселенность АО по Малликену - можно получить, подставляя в равенство (4.98) формулу (4.97).

Уже отмечалось, что n^M_a может принимать значения > 2, которые противоречат принципу Паули. Такие неразумные заселенности вносят отрицательный вклад в величину V_A. Очевидно, определение валентности атома через лёвдинские заселенности гибридных АО является более предпочтительным. В то же время не следует отказываться и от определения (4.101). Оно может быть полезным в тех случаях, когда в качестве результата расчета электронной структуры химического соединения приводятся заселенности АО по Малликену, а не по Лёвдину, причем опубликованной информации недостаточно, чтобы вычислить последние. Если перекрывание атомных орбиталей мало, то оба определения должны давать близкие результаты.

Систематическое исследование валентностей атомов от водорода до хлора было проведено Армстронгом, Стюартом и Перкинсом [29, 30]. Они показали, в частности, что валентности лития, бериллия и бора превышают номер группы периодической системы, в которой расположены эти Элементы (табл. 14). Интересные результаты были получены для фторидов фосфора, серы и хлора. Валентность указанных элементов оказывается близкой к числу присоединенных ими атомов фтора. В то же время индексы Виберга свидетельствуют о делокализованном характере связей в этих электронно-избыточных соединениях.

Таблица 14. Валентности атомов от лития до хлора в различных химических соединениях [30]

Значительный интерес представляет исследование валентности элементов, атомы которых обладают незаполненными d-оболочками. Армстронг, Фортуне и Перкинс [28] вычислили атомные заряды, индексы связей и валентности атомов в экзотической с точки зрения классической теории химической связи соли Цейзе К[C₂H₂PtCl₃], а также в комплексных ионах платины транс-[РtXCl₃]^- и транс-[PtX(NH₃)Cl₂]. Результаты вычислений приведены в табл. 15 и 16. Спектр валентности лежит в пределах от 2,3 до 2,9, причем ее связи с лигандами характеризуются существенно дробными индексами К ≈ 0,7. Пониженные по отношению к ординарной связи (К = 1) значения этих индексов обусловлены отчасти полярностью связей, отчасти их делокализацией. При сопоставлении валентных структур молекулы этилена в свободном состоянии и в составе соли Цейзе можно видеть, что валентность углерода и водорода при комплексообразовании практически не меняется. То же самое можно сказать и о формальных зарядах этих атомов. Заметно понижается кратность связи углерод-углерод, но вместе с тем в комплексном анионе [C₂H₂PtCl₃]^- реализуются СВЯЗИ платины с атомами углерода, характеризуемые значениями К_PtС = 0,33. Это обстоятельство влечет повышение валентности платины в соли Цейзе до 2,90 и обеспечивает неизменность валентности углерода.

Более детальное исследование валентной структуры комплексных соединений платины было проведено О. В. Сизовой и В. И. Барановским [24]. В частности, обобщая понятие валентности атома на многоатомные лиганды (L) и характеризуя σ- и π-донорную и акцепторную способность последних с помощью σ- и π-составляющих валентности V_L, они классифицировали одиннадцать важнейших лигандов по их донорной и акцепторной активности. Была рассмотрена также зависимость свойств лигандов от состава комплекса и взаимное влияние лигандов, передаваемое через орбитали центрального атома.