
2. Двойные растворы
При изучении зависимости состава пара от состава смесей двух жидкостей могут встретиться следующие случаи:
1. Жидкости растворимы друг в друге во всех отношениях, например вода и этиловый спирт.
2. Жидкости растворимы друг в друге не во всех отношениях, например вода и диэтиловый эфир (частично растворимые жидкости).
3. Жидкости практически нерастворимы друг в друге, например вода и ртуть.
Здесь мы ограничимся рассмотрением некоторых свойств растворов двух жидкостей, растворимых во всех отношениях и не обладающих минимальной или максимальной точкой кипения, т. е. не образующих азеотропных смесей (другие случаи будут более подробно рассмотрены в гл. VII).
При изучении свойств таких растворов прежде всего необходимо познакомиться с понятием "идеальный раствор", которым придется пользоваться и в дальнейшем.
"Идеальным раствором" двух жидкостей А и В называют такой раствор, в котором силы взаимодействия между молекулами веществ А и В равны силам взаимодействия между молекулами в чистых веществах А и В. Следовательно, вероятность испарения молекулы каждого вещества определяется только содержанием этого вещества в растворе. Математически это выражено законом Рауля: "относительное понижение давления пара данного вещества А численно равно молярной доле второго вещества В в смеси":
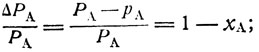
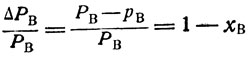
или
рА=РАха; рВ= РВхВ
где рА и рВ - парциальные давления паров веществ А и В в смеси;
РА и РВ - давления насыщенных паров чистых веществ при той же температуре, при которой определяют парциальные давления;
хА и хВ - молярные концентрации веществ А и В.
Так как хА+хВ=1, то, приняв хA равным х (х - молярная концентрация нижекипящего компонента в растворе), получим:
рА=РАх; рВ=РВ(1-х) (6)
Наиболее близки к идеальным растворы ближайших гомологов друг в друге.
Зависимость парциальных давлений компонентов и общего давления паров растворов двух жидкостей от состава растворов при постоянной температуре (изотермы) показана на рис. 5.
Для идеального раствора изменения парциального и общего давлений выражены прямыми линиями.
Свойства реальных растворов в большей или меньшей степени отклоняются от свойств идеальных растворов. Реальные растворы можно разбить на три группы:
1) растворы с положительным отклонением от закона Рауля (соответствующие кривые 1, 2, 3 на рис. 5 расположены выше прямых - выпуклые);
2) растворы с отрицательным отклонением от закона Рауля (соответствующие кривые 4, 5; 6 на рис. 5 расположены ниже прямых - вогнутые);
3) растворы, отклонение которых от закона Рауля может быть как положительным, так и отрицательным, в зависимости от концентрации компонентов.
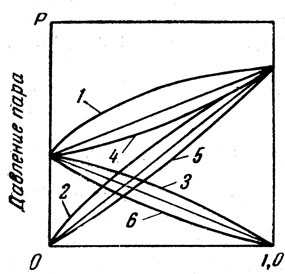
Рис. 5. Зависимость давления пара от состава смеси двух жидкостей: 1, 2, 3 - положительное отклонение от закона Рауля; 4, 5, 6 - отрицательное отклонение от закона Рауля; 1, 4 - общее давление пара над смесью; 2, 3, 5, 6 - парциальные давления
Из уравнений (6) следует, что для идеального раствора
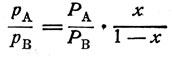 (7)
(7)В то же время по закону Дальтона "общее давление смеси газов равно сумме парциальных давлений ее ингредиентов" (компонентов) и парциальное давление каждого ингредиента (компонента) пропорционально общему давлению и концентрации его в паре:
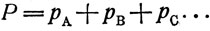
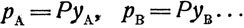 (8)
(8)где р - парциальное давление пара компонента;
Р - общее давление пара;
уА и уВ - молярные доли веществ А и В в паре.
Так как
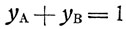
то
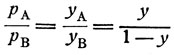 (9)
(9)где у - молярная концентрация нижекипящего компонента в паре.
Приравняв правые части уравнений (7) и (9) и обозначив - у или "относительную летучесть", через выводим уравнение
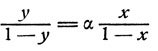 (10)
(10)Согласно первому закону Коновалова - Гиббса "пар относительно богаче тем компонентом, прибавление которого повышает общее давление пара системы" 1, 2. Отсюда следует, что во всех случаях α≥1; кроме того, из уравнения (10) видно, что относительная летучесть (α) представляет собой коэффициент пропорциональности, показывающий степень обогащения паровой фазы более летучим компонентом при однократном испарении. Для идеальных же и приближающихся к ним растворов под более летучим можно всегда рассматривать нижекипящий компонент.
Относительная летучесть α играет значительную роль в аналитических расчетах, связанных с ректификацией. Для идеальных растворов α вычисляют по величинам давлений паров чистых компонентов при одной и той же температуре, а для реальных - на основании экспериментальных данных по уравнению (10). Очень часто данные о зависимости состава пара от состава двойных смесей и даже о зависимости давления пара чистых веществ от температуры отсутствуют. В этих случаях приходится ограничиваться приближенными вычислениями, например по уравнению Трегубова3
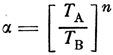 (11)
(11)где ТА и ТB - абсолютные температуры кипения веществ А и В.
Показатель степени n для углеводородов равен 11.
Для идеальных растворов величина а при постоянной температуре (изотермический процесс) не меняется с изменением состава. Однако чаще всего процессы ректификации протекают не при постоянной температуре, а при постоянном давлении (изобарически). В этих случаях температура кипения идеального раствора, а следовательно и относительная летучесть (α) зависят от состава. При расчетах обычно берут некоторое среднее геометрическое значение α при крайних температурах рассматриваемого интервала:
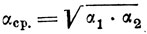
или
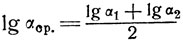 (12)
(12)где α1 и α2 относятся соответственно к температурам Т1 и Т2.
Для смесей жидкостей, к которым приложимы правило Трутона* и закон Рауля, α можно вычислить также, пользуясь уравнением Клаузиуса-Клапейрона и эмпирически найденными константами (см. обзорную статью8).
* (Правилом Трутона называют приближенное правило, по которому отношение молярной теплоты испарения к абсолютной температуре кипения жидкости постоянно и равно 21. Константа Трутона для полярных жидкостей значительно выше (подробнее см. 1))
Для двойных смесей углеводородов было выведено следующее уравнение:
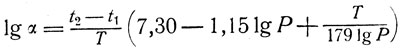 (13)
(13)В тех случаях, когда перегонки производят при давлении, близком к нормальному, уравнение (13) может быть приведено к более простому:
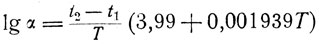
Величину а для неполярной жидкости с известным приближением можно найти по номограмме, построенной на основании уравнения (14) (см. приложение I).
Если имеются опытные данные о составе пара над растворами различных концентраций, то иногда бывает удобное (а для большинства смесей и точнее) пользоваться графическими методами расчета хода ректификации. Основой такого рода графических расчетов служит так называемая кривая равновесия. На рис. 6 (пунктир) изображена эта кривая в координатах ху, построенная на основании уравнения (10).
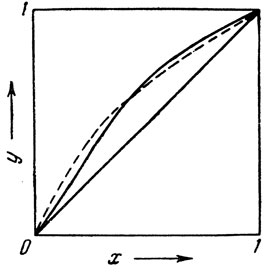
Рис. 6. Кривые равновесия: х - содержание нижекипящего компонента в жидкости; у - то же в паре. Пунктирная линия - изотермическая кривая; сплошная линия - изобарическая кривая
Так как уравнение (10) соответствует равновесному состоянию паровой и жидкой фаз, то кривые, изображенные на рис. 6, получили название "кривых равновесия". В самом деле каждая точка такой кривой определяет состав пара* (ордината), находящегося в равновесии с раствором определенной концентрации нижекипящего компонента (абсцисса); при этом естественно обе фазы имеют одну и ту же температуру. Пунктирная кривая на рис. 6 является изотермической кривой, построенной при постоянной величине α. Однако, как указывалось выше, больший интерес представляют изобарические кривые равновесия (сплошная кривая). Как видно из рис. 6, изобарические кривые не совпадают с изотермическими, что объясняется переменным значением величины α. Для реальных растворов это отклонение бывает еще значительнее. В дальнейшем под кривой равновесия мы всегда будем понимать изобарическую кривую.
* (Под "составом пара" здесь подразумевается содержание в нем нижекипящего компонента.)
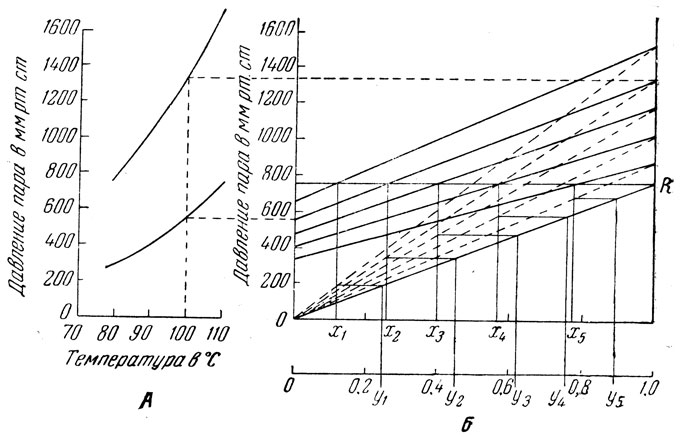
Рис. 7. График для построения кривой равновесия
Чтобы построить кривую равновесия по экспериментальным данным, откладывают на оси абсцисс содержание нижекипящего компонента в жидкости, а на оси ординат - содержание нижекипящего компонента в паре и наносят по соответствующим данным точки.
Для идеальных растворов или близких к ним кривую равновесия можно построить также графическим методом по кривым давлений пара чистых веществ. С этой целью строят вспомогательный график (рис. 7, А и Б). В левой части этого графика (рис. 7, А) наносят кривые давлений паров чистых веществ.
На рис. 7, А нанесены кривые давлений паров чистых бензола и толуола (ордината - давление, абсцисса - температура). Затем строят график (рис. 7, Б) для смесей этих двух жидкостей. На оси абсцисс этого графика откладывают содержание нижекипящего компонента в жидкости, а на оси ординат, соответствующих 100% бензола (х=1; ось бензола) и 100% толуола (х=0; ось толуола), давление паров чистых веществ при выбранных температурах (например, при 85, 90, 100 и 105°).
Число температурных точек, взятых для построения изотерм, зависит от требуемого числа точек для построения кривой равновесия. Соединив точки, соответствующие одной температуре, получим семейство изотерм общего давления пара над смесью (на рис. 7, А и Б жирным пунктиром показано построение изотермы для 100°).
Прямые (тонкий пунктир), проведенные через основание оси толуола (Р=0; х=0), и точки, нанесенные ранее на оси бензола, представляют собой изотермы парциального давления бензола. Величину парциального давления толуола можно определить аналогичным) образом, а также по разности ординат общего давления пара и парциального давления пара бензола для смеси любого состава. Затем на высоте, соответствующей общему давлению (в данном случае 760 мм рт. ст.), проводят прямую, параллельную оси абсцисс, и соединяют точки 0 и R. Из точек пересечения изотерм полного давления с прямой, отвечающей 760 мм рт. ст., опускают вертикали. Они определят величину х, т. е. содержание нижекипящего компонента в жидкой фазе, кипящей при давлении 760 мм и соответствующей температуре.
Далее, из точки пересечения вертикали с однозначной изотермой парциального давления бензола (вертикаль, соединяющая изотермы полного и парциального давления) при одной температуре проводят ряд горизонталей до пересечения с диагональной прямой 0R. Абсциссы полученных таким образом точек определят у - содержание нижекипящего компонента в паровой фазе, образующейся при 760 мм рт. ст. и соответствующей температуре. Теперь остается нанести полученные точки, для которых найдены координаты х и у, на график, подобный изображенному на рис. 6.
Этим путем можно построить кривую равновесия при отсутствии непосредственных экспериментальных данных о зависимости состава пара от состава жидкости. Чем ближе раствор к идеальному и чем точнее выведена зависимость давления от температуры для индивидуальных веществ, являющихся компонентами двойной смеси, тем, естественно, правильнее будут наши расчеты. Способ Киреева35 (см. стр. 12) позволяет воспользоваться с этой целью минимальным количеством данных вплоть до одной температуры кипения вещества.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'