
1. Основы перегонки и ректификации
Простая перегонка является результатом однократного испарения жидкости и конденсации пара.
Чтобы графически определить содержание нижекипящего компонента в паре, образующемся при простой перегонке, например при перегонке жидкости из куба или колбы Вюрца, необходимо провести на диаграмме равновесия вертикаль на оси абсцисс (рис. 8), из точки х'к , соответствующей содержанию нижекипящего компонента в кубе. Ордината точки пересечения этой вертикали с кривой равновесия даст нам искомый ответ. Сконденсировав пар, мы получим дестиллат - жидкость с содержанием нижекипящего компонента х'д, равным у' (примерное содержание нижекипящего компонента в первых каплях дестиллата). По мере выкипания жидкости содержание нижекипящего компонента в кубе изменяется от х'к до х''к в отгоняемом дестиллате от x'д до х"д. Понятно, что в полученном дестиллате, обогащенном по сравнению с загрузкой* нижекипящим компонентом, содержание последнего выражается некоторой величиной, лежащей между х'д и xд, а его содержание в остатке** куба, обогащенном вышекипящим компонентом, - величиной, лежащей между х'к и x''. Чтобы получить чистые компоненты, смесь приходится многократно подвергать простой перегонке. При каждой перегонке дестиллат все более обогащается нижекипящим, а остаток вышекипящим компонентом (подробнее см. 1, 2, 3, 4). Эта операция - много, кратная перегонка - называется обычно простой фракционированной перегонкой, или дробной перегонкой. Дробная перегонка - весьма трудоемкая операция, сопровождающаяся значительными потерями вещества.
* (Загрузка - жидкость, загруженная в куб для перегонки.)
** (Остаток - жидкость, оставшаяся в кубе после перегонки. Жидкость же, находящаяся в кубе во время перегонки, обозначена в книге термином "жидкость в кубе".)
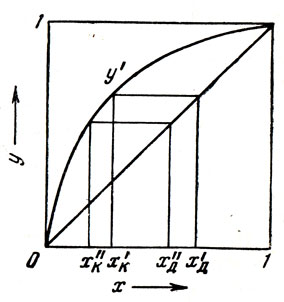
Рис. 8. График процесса простой перегонки: х - содержание нижекипящего компонента в жидкости; у - то же в паре
Удобнее и экономнее проводить разделение жидкостей при помощи ректификации. Известны два способа проведения ректификации: непрерывный, применяемый в промышленности, и периодический, которым пользуются обычно в лабораториях.
При непрерывной ректификации подогретая до кипения смесь подается в среднюю часть колонны*. Нижекипящий компонент отбирается в верхней части колонны в виде дестиллата; вышекипящие компоненты отбираются из куба. Скорость питания колонны, т. е. количество смеси, вводимой в нее в единицу времени, равна сумме скоростей отбора дестиллата и остатка из куба. Отличительной чертой непрерывной ректификации, как и всякого процесса в проточной системе, является динамическое равновесие, которое устанавливается по всей колонне: составы жидкости, подаваемой на питание, дестиллата и жидкости из куба, а также состав жидкости и пара и условия процесса в любом месте колонны не изменяются во времени. Для разделения смеси по способу непрерывной ректификации необходимо иметь столько же последовательно соединенных колонн, сколько компонентов выделяется из смеси, не считая жидкости в кубе последней колонны. Каждая колонна выделяет только один нижекипящий компонент в виде дестиллата. Все оставшиеся вышекипящие компоненты из куба подаются на питание следующей колонны.
* (Колонна - аппарат для ректификации в заводских условиях. Колонка - лабораторный аппарат для ректификации. При теоретических рассуждениях аппарат для ректификации обозначают термином "колонна".)
При периодической ректификации перегоняемая смесь загружается в куб колонны. Компоненты смеси один за другим отбираются в виде дестиллата в порядке повышения их температур кипения (или понижения летучести); таким образом, для разделения смеси достаточно одной колонны. При этом способе ректификации все условия процесса и состав перегоняемой жидкости в любом месте системы изменяются по мере отбора дестиллата. Если же колонна периодической ректификации работает с полным возвратом, т. е. без отбора дестиллата, то в ней устанавливается равновесие, не изменяющееся в дальнейшем во времени.
Процесс работы колонны в условиях равновесия (непрерывная ректификация или периодическая при полном возврате) легко поддается математической обработке. Исследование же процесса периодической ректификации при отборе дестиллата на много сложнее и еще не получило хорошего математического выражения.
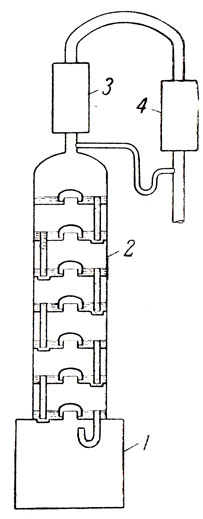
Рис. 9. Схема ректификационной тарельчатой колонны: 1 - куб; 2 - собственно колонна; 3 - конденсатор; 4 - холодильник
Чтобы ознакомиться с процессом ректификации, представим себе в общих чертах работу тарельчатой колонны (рис. 9). Тарельчатая колонна состоит из куба в котором жидкость нагревается до кипения, собственно колонны 2 и конденсатора 3. Конденсат - продукт конденсации пара - может или полностью возвращаться назад в колонну в виде "орошения"* (полный возврат**, или разделяться на орошение и отбираемый дестиллат (частичное орошение). Колонна 2 представляет собой цилиндр, в котором расположены друг под другом днища, называемые также тарелками. На каждой тарелке задерживается известное количество жидкости - флегмы***, избыток которой сливается на нижележащую тарелку через слив. Поднимающийся в колонне пар проходит через слои флегмы, находящиеся на тарелках. При этом на каждой тарелке происходит обмен компонентов между фазами: нижекипящие компоненты переходят из жидкости в пар, вышекипящие - из пара в жидкость. Пройдя всю колонну, пар обогащается нижекипящим, а жидкость вышекипящим компонентом. Именно в этом процессе, т. е. в обмене компонентами между жидкостью и паром, и состоит сущность ректификации.
* ("Орошением" называют жидкость, стекающую при перегонке из конденсатора в заводскую колонну, или из головки в центральную трубку лабораторной колонки. Величиной орошения называется число миллилитров жидкости, стекающей из головки в колонку во время ее работы за один час, или же число капель этой жидкости, стекающей из головки в центральную трубку за одну минуту.)
** (Или полное орошение.)
*** (Флегмой называется жидкость, находящаяся в колонке во время перегонки. Величиной флегмы называется число миллилитров жидкости, стекающей из колонки в куб во время ее работы за один час, или же число капель в минуту.)
В идеальной тарельчатой колонне при полном возврате пара на каждой тарелке (и следовательно, по всей колонне) устанавливается равновесие между паровой и жидкой фазами, состав которых определяется кривой равновесия. Таким образом, на каждой тарелке как бы происходит акт однократного испарения жидкости данного состава.
В реальных тарельчатых колоннах полное равновесие между паром и флегмой никогда не устанавливается. Поэтому при технологических расчетах приходится вводить поправочный коэффициент, зависящим от конструкции тарелки и показывающий, насколько равновесие, устанавливающееся на тарелке, отклоняется от теоретического, определяемого по кривой.
Процесс непрерывной ректификации, осуществляемый в идеальной колонне, удобнее всего разобрать, пользуясь графическим методом (см. 3, 4). Рассмотрим для этого кривую равновесия ОАВ (рис. 10). Предположим, что в кубе находится смесь двух жидкостей, содержащая хк молярных долей нижекипящего компонента; тогда содержание нижекипящего компонента во флегме, стекающей с первой тарелки идеальной колонны, как уже указывалось, равно его содержанию в поступающем снизу паре, т. е. х1=у1 Чтобы найти содержание нижекипящего компонента в паре, поднимающемся с первой тарелки, необходимо определить ординату точки на кривой равновесия, имеющей абсциссу х1, для этого надо провести вертикаль из точки х1. Тот же результат мы получим, если проведем из точки А (координаты хку1) прямую параллельно оси абсцисс до пересечения с диагональю графика, а из точки пересечения А1 проведем вертикаль до пересечения с кривой равновесия (точка В). Абсциссы каждой из последовательно найденных таким образом точек на кривой равновесия будут выражать содержание нижекипящего компонента во флегме, стекающей с соответствующей тарелки, а ординаты этих точек - его содержание в паре, поднимающемся к ней. Каждая ступенька (например, АА1В) выразит результат работы одной теоретической тарелки при полном возврате пара, а работа всей идеальной колонны выразится ломаной линией. Тарелки идеальной колонны, отвечающие теоретическому расчету (например, в приведенном выше случае для полного возврата), называются теоретическими тарелками (ТТ).
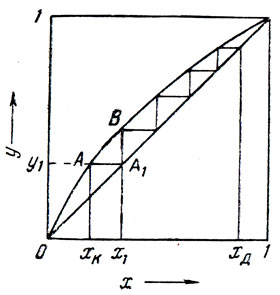
Рис. 10. График процесса ректификации: х - содержание нижекипящего компонента в жидкости; у - то же в паре
Известно, что наряду с тарельчатыми колоннами в промышленности часто, а в лабораториях почти всегда применяют так называемые насадочные колонны (или колонки), в которых тарелки заменены насадками - устройствами, увеличивающими поверхность соприкосновения пара и флегмы. Понятие "теоретическая тарелка" выведено из рассмотрения работы идеальной тарельчатой колонны; тем не менее все положения и закономерности, справедливые для тарельчатых колонн, можно с полным правом отнести к любым другим перегонным" приборам, в том числе и к насадочным колоннам различного устройства. В последних можно рассматривать участки, выполняющие работу одной теоретической тарелки.
Эффективность лабораторных колонок, как тарельчатых, так и насадочных, определяется числом теоретических тарелок (N) такой идеальной колонны, которая дала бы ту же степень обогащения дестиллата нижекипящим компонентом, что и данная реальная колонна. Эффективность колонн было предложено определять высотой, эквивалентной одной теоретической тарелке - ВЭТТ (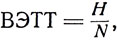 , где Н - высота колонны). Однако числа участков, выполняющих работу одной тарелки, непостоянно, а распределение их по длине колонны и высота каждого участка зависят от условий работы. Для колонок одного и того же типа, но разной высоты ВЭТТ будет различным. Поэтому, давая характеристику эффективности лабораторных колонок, недостаточно приводить величину ВЭТТ или число теоретических тарелок на метр длины (величина, обратная ВЭТТ), а необходимо, кроме того, указывать высоту колонки и число теоретических тарелок.
, где Н - высота колонны). Однако числа участков, выполняющих работу одной тарелки, непостоянно, а распределение их по длине колонны и высота каждого участка зависят от условий работы. Для колонок одного и того же типа, но разной высоты ВЭТТ будет различным. Поэтому, давая характеристику эффективности лабораторных колонок, недостаточно приводить величину ВЭТТ или число теоретических тарелок на метр длины (величина, обратная ВЭТТ), а необходимо, кроме того, указывать высоту колонки и число теоретических тарелок.
Пользоваться ВЭТ (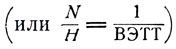 ) целесообразно лишь для приблизительного сравнения эффективности колонок или насадок различных конструкций и высоты. Минимальное число теоретических тарелок, т. е. число их, необходимое для разделения двойной смеси при полном возврате и бесконечно малой задержке, можно вычислить, как было выше показано, графически.
) целесообразно лишь для приблизительного сравнения эффективности колонок или насадок различных конструкций и высоты. Минимальное число теоретических тарелок, т. е. число их, необходимое для разделения двойной смеси при полном возврате и бесконечно малой задержке, можно вычислить, как было выше показано, графически.
Алгебраически же минимальное число теоретических тарелок можно вычислить по уравнению
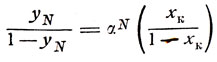 (15)
(15)где N - число теоретических тарелок.
Уравнение (15) выведено путем преобразования уравнения (10).
Решив уравнение (15) относительно уN или N, получим:
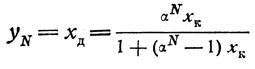 (16)
(16)и
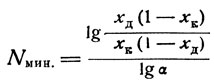 (17)
(17)Поскольку в рассматриваемом случае речь идет о минимальном числе теоретических тарелок, это число в уравнении (17) обозначено через Nмин.
Уравнения (15), (16) и (17) связывают между собой, содержание нижекипящего компонента в паре вверху колонны, в головке колонны, а значит и в дестиллате, его содержание в жидкости в кубе и число теоретических тарелок. Эти уравнения пригодны для разного рода расчетов (как, например, для определения N) при условии, что состав жидкости в кубе или состав дестиллата не изменяется во время работы.
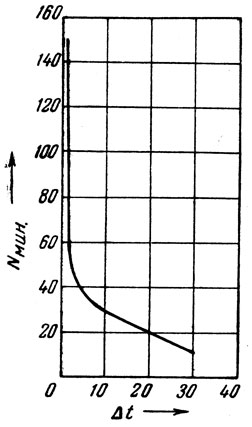
Рис. 11. Зависимость между разностью температур кипения компонентов (Δt) двойной смеси и минимальным числом теоретических тарелок (Nмин.)
Так как lqα пропорционален Δt [см. уравнение (13)], то Nмин.≈1/t. На рис. 11 показана приближенная кривая зависимости между разностью температур кипения компонентов и потребным для разделения смеси минимальным числом теоретических тарелок. Число теоретических тарелок весьма приближенно можно вычислить по уравнению
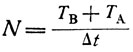 (17а)
(17а)где ТА и ТB - абсолютные температуры кипения компонентов А и В;
Δt - разность их температур кипения.
Однако при периодической ректификации, обычно применяющейся в лабораториях, когда состав жидкости в кубе и состав дестиллата изменяются в течение работы, часто бывает удобнее пользоваться другим уравнением, приведенным Оболенцевым и Фростом39
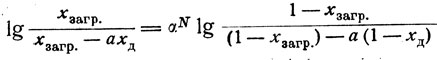 (18)
(18)где а - молярная доля дестиллата от загрузки;
xзагр. - содержание нижекипящего компонента в загрузке;
хд - содержание нижекипящего компонента в дестиллате.
Так как в реальных условиях полный возврат не может иметь места, а задержка имеет всегда определенную конечную величину, минимальное число тарелок, разумеется, недостаточно для разделения смеси.
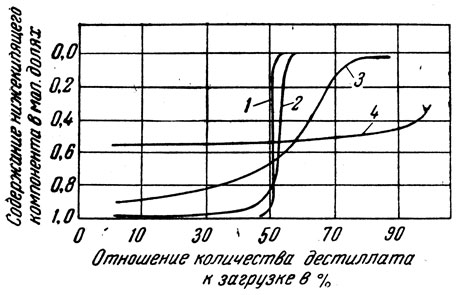
Рис. 12. Рассчитанные кривые разгонки двойной смеси: 1-Е-807; 2-Е=86; 3-Е=9,3; 4-Е=1,25
Как можно видеть из уравнения (18), содержание нижекипящего компонента в дестиллате зависит от отношения количества дестиллата к количеству загрузки и от αN. Эта величина названа "фактором фракционирования"; обозначается она через Е.
На основании уравнения типа (18) можно40, 41 составить ряд графиков, наглядно показывающих зависимость между фактором фракционирования Е (а значит и минимальным числом теоретических тарелок относительной летучестью) и точностью разгонки двойной смеси.
На рис. 12 приведены четыре рассчитанные кривые разгонок двойной смеси, содержащей 50% нижекипящего компонента при разных значениях Е (без учета заполнения, при полном возврате). Кривая 1 при Е=807 выражает весьма точную разгонку, при которой промежуточная фракция составляет 1 - 2% от взятой смеси. Так как Е=αN, то такое разделение может быть достигнуто или простой перегонкой из колбы Вюрца (N=1) смеси двух веществ, для которой α=807 (разность температур кипения Δt=200-250°), или смеси веществ, для которой α=1,25(Δt=6-9°) на колонке в 30 теоретических тарелок. Ниже приведены цифры, характеризующие кривые рис. 12.

Зависимость между величиной промежуточной фракции и фактором Е показана в табл. 2 и на рис. 13.

Таблица 2. Зависимость между фактором фракционирования и величиной промежуточной фракции
Практический интерес представляют разгонки, в которых промежуточная фракция составляет менее 10% и более 0,5% от взятой смеси. Это определяет довольно узкий диапазон для фактора Е.
Для данной смеси с определенным значением a и данной колонны с определенным значением N величина промежуточной фракции зависит в известной мере от времени, требующегося для перегонки смеси, т. е. чем точнее разгонка, тем больше обычно требуется времени. Поэтому в каждом конкретном случае следует ограничиться некоторой минимально допустимой точностью и максимально допустимым временем.
Действительно, поскольку полученные кривые зависимости величины промежуточной фракции от фактора Е представляют собой гиперболы, уменьшение фактора фракционирования в определенных пределах приводит, как это видно из рис. 13, к быстрому росту промежуточной фракции, так как кривые асимптотически приближаются к оси ординат. С другой стороны, увеличение Е в области больших значений весьма мало влияет на уменьшение промежуточной фракции, так как кривые асимптотически приближаются к оси абсцисс. Оптимальные пределы фактора фракционирования зависят от тех границ состава, в которых собирается промежуточная фракция.
Так, например, в тех случаях, когда собирают промежуточную фракцию при содержании нижекипящего компонента в дестиллате хд от 0,9 до 0,1 (т. е. начинают собирать как только содержание нижекипящего компонента упадет до 90 % и кончают собирать после того, как содержание вышекипящего компонента достигнет 90%), целесообразными пределами фактора фракционирования Е являются величины 55 и 800.
В тех же случаях, когда промежуточную фракцию собирают при содержании в дестиллате нижекипящего компонента, равном от 0,99 до 0,01, рациональными пределами Е являются величины 520 и 3500.
Если идеальная колонна начинает работать с частичным возвратом, то установившееся в ней ранее при полном возврате равновесие нарушается и она приходит к новому "псевдоравновесному" состоянию. Действительно, с дестиллатом из колонны уходит часть нижекипящего компонента. Следовательно, при отборе дестиллата орошение вносит в колонну меньшее количество нижекипящего компонента в единицу времени, чем это было при полном возврате; содержание нижекипящего компонента во флегме на тарелках таким образом уменьшается.
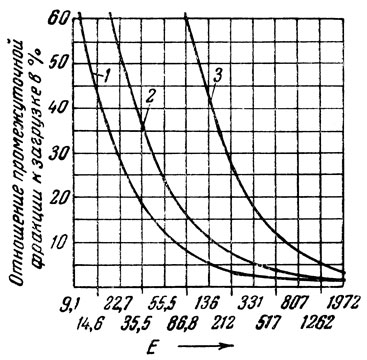
Рис. 13. Зависимость величины промежуточной фракции от фактора фракционирования (см. табл. 2): 1 - отбор промежуточной фракции от х =0,1 до х=0,9; 2 - отбор промежуточной фракции от х=0,05 до х=0,95; 3 - отбор промежуточной фракции от х=0,01 до х=0,99
Математический анализ показывает, что для графического изображения работы идеальной колонны при частичном возврате необходимо на диаграмме равновесия провести прямую, называемую линией концентрации или рабочей линией (рис. 14, прямая АВ); прямая эта отвечает уравнению
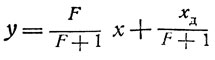
где Р - флегмовое число или отношение количества орошения к количеству дестиллата за один и тот же промежуток времени. Далее производится построение, аналогичное описанному выше (см. рис. 10), но горизонтальные отрезки прямых проводят при этом до пересечения с рабочей линией. В результате получается "лесенка", изображенная на рис. 14 сплошной ломаной линией. Для сравнения на рис. 14 пунктирной "лесенкой" показано построение, отвечающее ректификации с бесконечно большим флегмовым числом.
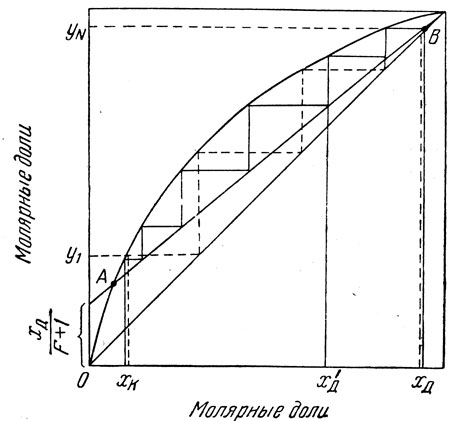
Рис. 14. Расчет процесса ректификации на диаграмме равновесия
Поскольку свободным членом уравнения (19) является одночлен 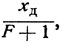 , а коэффициентом при х - одночлен
, а коэффициентом при х - одночлен 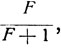 , то следовательно, рабочая линия отсекает на оси ординат отрезок, равный
, то следовательно, рабочая линия отсекает на оси ординат отрезок, равный 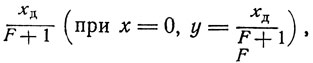 , а наклон прямой зависит от флегмового числа
, а наклон прямой зависит от флегмового числа 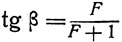 (в этом выражении β - угол наклона рабочей линии). Рабочая линия пересекает диагональ диаграммы равновесия в точке, абсцисса которой равна xд. Чем больше флегмовое число F, тем больше наклон прямой, и при F, равном ∞, рабочая линия совпадает с диагональю графика. С другой стороны, флегмовое число имеет свой минимальный предел, при котором теоретически еще возможно получить из жидкости в кубе, при данном содержании нижекипящего компонента, отгон требуемой концентрации. Рабочая линия, отвечающая минимальному флегмовому числу, пересекает кривую в точке, абсцисса которой равна хк. Минимальное флегмовое число вычисляют по приведенным ниже уравнениям (см.3, 4 и обзорную статью8):
(в этом выражении β - угол наклона рабочей линии). Рабочая линия пересекает диагональ диаграммы равновесия в точке, абсцисса которой равна xд. Чем больше флегмовое число F, тем больше наклон прямой, и при F, равном ∞, рабочая линия совпадает с диагональю графика. С другой стороны, флегмовое число имеет свой минимальный предел, при котором теоретически еще возможно получить из жидкости в кубе, при данном содержании нижекипящего компонента, отгон требуемой концентрации. Рабочая линия, отвечающая минимальному флегмовому числу, пересекает кривую в точке, абсцисса которой равна хк. Минимальное флегмовое число вычисляют по приведенным ниже уравнениям (см.3, 4 и обзорную статью8):
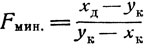 20
20где ук соответствует у1 на рис. 14.
Если вместо содержания нижекипящего компонента в паре, находящемся в кубе, в уравнение (20) подставить содержание нижекипящего компонента в жидкости куба, то уравнение (20) примет следующий вид:
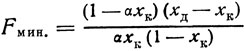 21
21Минимальное флегмовое число можно также определить по номограмме, приведенной в приложении I.
Так как при бесконечно большом флегмовом числе возврат оказывается полным, то число теоретических тарелок, необходимых для получения дестиллата заданной концентрации, при бесконечно большом флегмовом числе, является минимальным. С уменьшением флегмового числа необходимое для данной степени обогащения дестиллата число теоретических тарелок увеличивается. Это хорошо видно из сравнения пунктирной и сплошной ломаных линий на рис. 14. Так, для получения того же эффекта при разгонке с полным орошением потребовалось 4 теоретические тарелки, а при отборе дестиллата с флегмовым числом F - 6 теоретических тарелок. При работе колонны с минимальным флегмовым числом требуется бесконечно большое число теоретических тарелок. Таким образом, и флегмовое число и число теоретических тарелок изменяются от некоторого минимального значения до бесконечности.
Установлено43, что все экспериментальные данные хорошо укладываются на одну кривую, если по оси абсцисс отложить 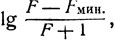 , а по оси ординат
, а по оси ординат 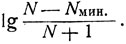 .
.
Правая часть номограммы для вычисления (см. приложение I, рис. 80) построена согласно такому корреляционному графику.
Из сказанного совершенно ясно, что при данном составе жидкости в кубе можно достичь одной и той же степени обогащения дестиллата, уменьшая в известных пределах число теоретических тарелок колонки и увеличивая соответственно флегмовое число.
Лонгинов и Зейфман42 установили, что увеличивать флегмовое число при ректификации целесообразно лишь до некоторого предела.
Существует мнение41, что флегмовое число, как правило, должно приближаться к числу теоретических тарелок колонки, причем нецелесообразно устанавливать F большим, чем 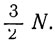 , или меньшим, чем
, или меньшим, чем 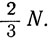 . Иначе говоря, флегмовое число должно находиться в пределах от
. Иначе говоря, флегмовое число должно находиться в пределах от 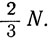 до -
до - 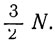 .
.
Действительно, если флегмовое число уже равно 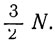 , то по мере его дальнейшего увеличения (что сопровождается увеличением времени, потребного для разгонки) степень влияния его на точность разгонки уменьшается; при уменьшении же F ниже
, то по мере его дальнейшего увеличения (что сопровождается увеличением времени, потребного для разгонки) степень влияния его на точность разгонки уменьшается; при уменьшении же F ниже 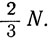 эффективность разгонки резко падает.
эффективность разгонки резко падает.
Недавно Крылов44 предложил весьма интересный метод аналитического расчета числа теоретических тарелок в рабочих условиях, т. е. при частичном орошении. Для двойных растворов Крылов вывел следующие уравнения:
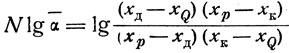 (22)
(22)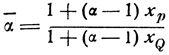 (23)
(23)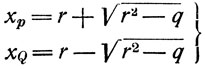 (24)
(24)В этих уравнениях
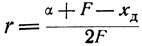
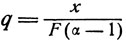
Ранее приведенное уравнение (17) является частным случаем уравнения Крылова, так как при полном возврате, для которого выведено уравнение (17):
хр=1 и хQ=0
Подставляя эти значения хр и хQ в уравнение (22), получаем уравнение, тождественное уравнению (17):
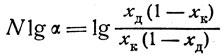
Уравнения (22) и (23) дают возможность вычислить необходимое число теоретических тарелок в рабочих условиях в зависимости от задач разгонки и построить соответствующую номограмму.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'