А. Описание решетки кристалла

§ 1. Группа трансляций - решетка кристалла

Трехмерная периодичность - обязательное свойство структуры идеального кристалла. Выберем три неком-планарных трансляционных направления в качестве координатных осей. Обозначим минимальный трансляционный вектор вдоль оси X через а, вдоль оси Y - через b, вдоль оси Z - через с. Допустим (временно, до более глубокого анализа симметрии кристаллической структуры), что оси X, Y и Z выбраны так, что параллелепипед, построенный на векторах а, b и с, не содержит (внутри себя или на своих гранях) точек, трансляционно эквивалентных его вершинам. Понятно, что самосовмещение пространства должно достигаться и при любом последовательном повторении любой из трех "первичных" трансляций а,b, с, т. е. при переносе на любой вектор t_mnp, удовлетворяющий условию

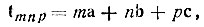(1)

где m, n, p - любые целые числа.

Такую совокупность векторов t_mnp называют трансляционной группой кристалла (трансляционной подгруппой пространственной группы симметрии) или коротко-решеткой кристалла.

Трансляционную группу обычно изображают в виде совокупности точек, отмечающих концы всех трансляционных векторов, отложенных от общего начала координат (рис. 1, а, б). Нетрудно видеть, что система таких точек, удовлетворяющая условию (1), действительно располагается по узлам трехмерной решетки.

Отметим, что термин "решетка" применяется в кристаллохимии в двух разных значениях. В теории симметрии решетка - это совокупность трансляций; узлы решетки - математические точки, а не материальные частицы. В описательной кристаллохимии и особенно в кристаллофизике тот же термин часто используется для пояснения способа размещения всех или части атомов кристалла. Во избежание путаницы можно рекомендовать применение термина "решетка кристалла" или "кристаллическая решетка" только в рамках теории симметрии и "атомная решетка" (или "атомная подрешетка", если имеется в виду лишь часть атомов) - при описании размещения атомов в кристаллической структуре. Такое терминологическое разграничение важно, в частности, потому, что некоторые поясняющие термины (такие, как объемно центрированная или гранецентрированная решетка) могут не совпасть применительно к симметрии и к размещению атомов определенного сорта в одной и той же кристаллической структуре.

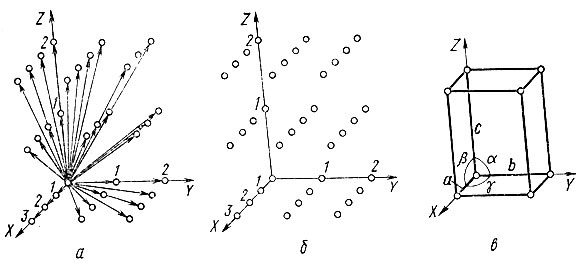
Рис. 1. Изображение трансляционной группы (решетки) кристалла (а и б); параллелепипед повторяемости (в)

В соответствии с соотношением (1) для задания решетки кристалла в общем случае необходимо указать три векторных параметра а, b, с или шесть скалярных: размеры трансляций а, b, с и углы между их направлениями α, β, γ (α - угол между осями Y и Z; β - между X и Z; γ - между X и Y, рис. 1, в). Эти шесть величин называются параметрами решетки, а построенный на них параллелепипед - параллелепипедом повторяемости. Если оси X, Y, Z выбраны в соответствии с определенными принятыми в кристаллографии правилами (см. ниже гл. I, § 10), то параллелепипед повторяемости называют элементарной ячейкой кристалла.