§ 2. Индексы узлов, узловых рядов и узловых сеток решетки кристалла

Трансляционная система кристалла играет определяющую роль в геометрии дифракционного эффекта, возникающего при прохождении рентгеновских лучей через кристалл. Параметры и другие характеристики решетки входят во все основные формулы рентгеноструктурного анализа. Поэтому следует познакомиться с некоторыми вспомогательными понятиями и обозначениями "решетчатой кристаллографии". К таковым относятся понятия узловых рядов и узловых сеток и вспомогательный образ - обратная решетка.

Индексы узлов.

При описании решетки кристалла один из ее узлов выбирают за начало координат. Все узлы решетки нумеруют по порядку вдоль координатных осей. Каждый узел характеризуется, следовательно, тремя целыми числами m, n и p называемыми индексами узла. Их совокупность, записанная в форме ·mnp·, называется символом узла. Любую трансляцию можно записать с помощью вектора, проведенного из начала координат в соответствующий узел ·mnp·, в виде

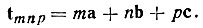
Аналогичным образом вектор, проведенный из начала координат элементарной ячейки в любую ее точку, можно представить как

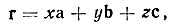(2)

где x, y, z - числа, меньшие единицы, имеют смысл координат некоторой точки ячейки, выраженных в долях ребер ячейки а, b и с соответственно (относительные координаты точки).

Индексы узловых рядов.

В решетке можно провести множество узловых рядов разной ориентации (рис. 2, а). Семейству (серии) параллельных друг другу узловых рядов приписывают в качестве символа индексы ближайшего к началу координат узла, через который проходит узловой ряд, непосредственно пересекающий начало координат. Серия узловых рядов обозначается [mnp]. В решетке, изображенной на рис. 2, а, показаны узловые ряды четырех разных серий. Их символы: [210], [010], [110] и [120]^*.

^* (Подразумевается, что изображенные ряды лежат в плоскости XY кристалла. Поэтому третий индекс всюду равен нулю.)

Индексы узловых сеток.

В любой решетке можно провести множество серий узловых сеток разной ориентации (рис. 2, б). Каждая серия характеризуется своим наклоном к координатным осям и своим межплоскостным расстоянием.

Наклон серии сеток передается ее символом (hkl). Индексами серии сеток h, k и l называют число частей, на которое разбиваются ребра элементарной ячейки (а, b и с соответственно) данной серией сеток. Так, на рис. 2, б приведены сетки с индексами (100), (110), (320)^*.

^* (Предполагается, что показанные решетки сетки параллельны третьей оси Z кристалла, т.е. не пересекает ребро c. Поэтому третий индекс всюду равен нулю.)

Будем, как и ранее, считать, что оси Х, Y и Z выбраны так, что параллелепипед, построенный на параметрах a, b, c остается "пустым" - не содержит дополнительных узлов ни в своем объеме, ни на гранях. Такую решетку называют примитивной.

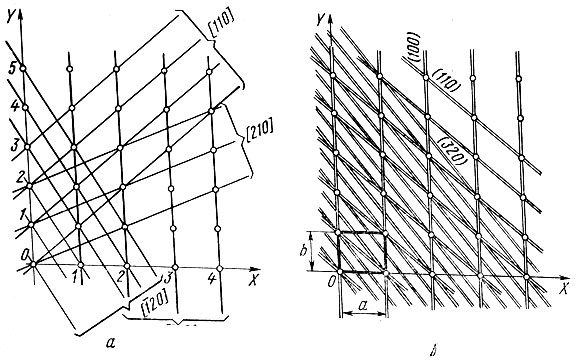
Рис. 2. Серии узловых рядов (а) и серии узловых сеток решетки (б)

Докажем следующее важное положение: в примитивной решетке индексы любой серии сеток (hkl) суть числа, не имеющие общего множителя.

Сетка, относящаяся к серии (hkl) и ближайшая к началу координат, отсекает на осях отрезки a/h, b/k и с/l. Уравнение этой сетки

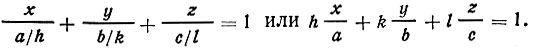
Сетка является узловой, т. е. проходит через некоторые точки с координатами x=ma, y=nb, z=pc, где m, n, p - целые числа. Следовательно, должно удовлетворяться равенство mh+nk+pl=1 с целочисленными m, n, p и h, k, l. Это возможно лишь при условии, что mh, nk, pl и, следовательно, h, k, l не имеют общего множителя.

Межплоскостные расстояния.

Вторая характеристика серии узловых сеток - межплоскостное расстояние d_hkl - зависит как от индексов этой серии сеток, так и от параметров решетки. В общем случае эта зависимость имеет вид^*

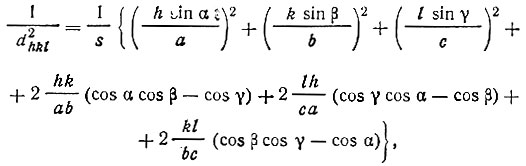(3)

где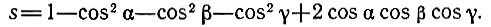

Она, естественно, упрощается при повышении симметрии кристалла. Так, например, если координатная система ортогональна, т. е. α= β= γ=90° (ромбическая симметрия), то

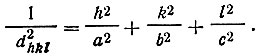
Если, кроме того, a=b (тетрагональная симметрия), то

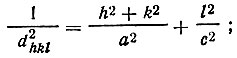
в случае a=b=c (кубическая симметрия)

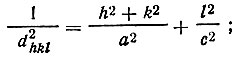
Эти формулы имеют практическое значение. Они позволяют определять индексы узловых сеток и параметры решеток по межплоскостным расстояниям, найденным из рентгенограмм (см. § 7 гл. И).

^* (Вывод формулы - см. § 3.)