§ 3. Обратная решетка

В физике часто приходится иметь дело со скалярными произведениями векторов: (rH)=rHcosφ, где φ - угол между векторами. Как известно, при использовании ортогональной системы координат с одинаковыми единичными векторами выражение скалярного произведения через компоненты векторов r_X, r_Y, r_Z и H_X, H_Y, H_Z имеет очень простой вид:

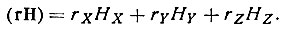(4)

Если, однако, система не ортогональна и (или) единицы измерения по осям различны, то представление (rH) через компоненты значительно усложняется. Чтобы сохранить запись в форме (4), помимо основной координатной системы вводится вторая, так называемая взаимная или обратная система координат, и один из векторов выражается через компоненты в основной системе, другой - через свои компоненты в обратной системе.

В частности, к этому средству приходится прибегать и в структурной кристаллографии.

Осевые орты взаимной системы a*,b*, c* определяются через осевые векторы кристаллографической системы a, b, c единичной матрицей скалярных произведений:

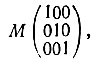
т. е. соотношениями

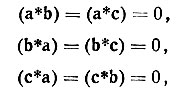(5)

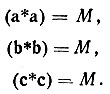(6)

Если теперь вектор r представить в кристаллографической системе 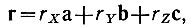, а вектор H - во взаимной системе 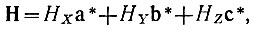, то, учитывая соотношения (5) и (6), снова получим 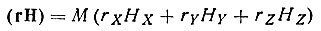, если M=1, и

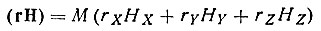(7)

в общем случае.

Геометрический смысл соотношений (5) и (6) очень прост.

Соотношения означают, что вектор а* перпендикулярен и вектору b и вектору с, т. е. плоскости YZ. Аналогично, вектор b* перпендикулярен плоскости XZ, а вектор с* - плоскости XY.

Соотношение (a*a)=М означает, что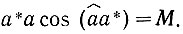
. Но 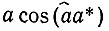-это межплоскостное расстояние между параллельными гранями YZ элементарной ячейки, т. е. межплоскостное расстояние d₁₀₀ (рис. 3, а). Следовательно, длина осевого вектора обратной решетки равна

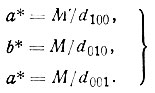(8)

По своей длине осевые орты a*, b*, c* обратны межплоскостным расстояниям серии плоскостей (100),(010) и (001) соответственно (с масштабным коэффициентом М).

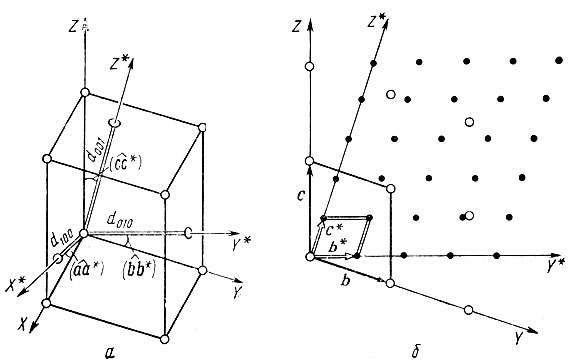
Рис. 3. Направление осей обратной координатной системы (а); построение обратной решетки (б)

Используем осевые орты а*, b*, c* для построения второй решетки, т. е. введем систему точек ·hkl·*, удовлетворяющих условию

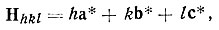(9)

где h, k, l - любые целые числа (рис. 3, б).

Решетку, построенную таким образом, называют обратной по отношению к кристаллографической. Этот вспомогательный геометрический образ широко используется в рентгеноструктурном анализе для интерпретации рентгенограмм.

На рис. 4, а изображены прямая и обратная решетки (условно взяты двумерные решетки; третий индекс каждого узла можно считать равным нулю). В обратной решетке проведен узловой ряд через точки ·110·*, ·220·*, ·330·*, т. е. узловой ряд [110]*. На том же рисунке показана серия плоскостей основной решетки, имеющая те же индексы (110). Как видно, они взаимно перпендикулярны. На рис. 4, б то же построение относится к узловому ряду [310]* обратной решетки и серии узловых сеток (310) основной решетки. Узловой ряд [310]* снова перпендикулярен плоскости (310). Кроме того, легко видеть, что чем больше длина вектора H_hkl обратной решетки, тем меньше межплоскостное расстояние в соответствующей серии плоскостей d_hkl основной решетки.

Рис. 4. Взаимные ориентации узловых рядов обратной решетки и узловых сеток решетки кристалла: а - сетки (110) и узловой ряд [110]*; б -сетки (310) и узловой ряд [310]*

В общем виде справедливо следующее соотношение.

Вектор Н_hkl, проведенный из начала координат в любой узел обратной решетки ·hkl·*, ближайший к началу в данном узловом ряду, всегда перпендикулярен узловой сетке основной (кристаллографической) решетки, имеющей те же индексы, а длина этого вектора |H_hkl| обратно пропорциональна межплоскостному расстоянию d_hkl. Если обозначить единичный по длине вектор нормали к серии плоскостей (hkl) через N_hkl (где |N|=1), то сформулированное свойство можно записать в виде соотношения

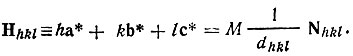(10)

Так как узловой ряд [hkl]* далее содержит узлы ·2h2k2l ·, ·3h3k3l ·, и т. д., то в более общей форме

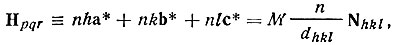(11)

где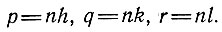

В скалярной форме 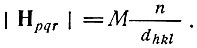. Соотношения (8) можно рассматривать как частные случаи этого общего соотношения.

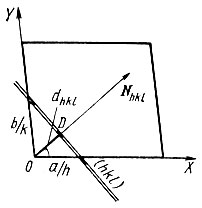
Рис. 5. К доказательству соотношения(11)

Для доказательства справедливости формулы (11) умножим обе части этого равенства скалярно на один из осевых векторов решетки кристалла, например а. С учетом соотношений (5) и (6) в левой части имеем

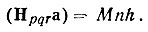(12)

В правой части соотношения (11) N_hkl по определению, есть единичный вектор нормали к серии плоскостей (hkl), следовательно, 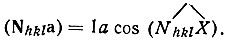. На рис. 5 изображена ближайшая к началу координат сетка (hkl) и проведена нормаль к ней N_hkl. На оси X отмечен отрезок a/h, отсекаемый этой сеткой, а на нормали N_hkl- расстояние d_hkl. Очевидно, что 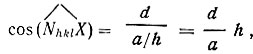, а вся правая часть (11)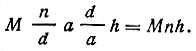. Повторив те же операции при скалярном

перемножении обеих частей равенства (11) на b и на с, убеждаемся, что все три компоненты (проекции на оси) векторов, представляющих левую и правую части равенства, совпадают. Значит, оба вектора Hpqr и 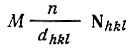равны по длине и совпадают по направлению.

Соотношения (10) и особенно (11) будут использованы в последующих разделах при выводе основных формул структурного анализа.

Соотношение (10) дает также основу для вывода формулы (3), связывающей межплоскостное расстояние некоторой серии плоскостей (hkl) с параметрами решетки a, b, c, α, β, γ. Положив М=1 и взяв скалярный квадрат от обеих частей равенства (10), получим

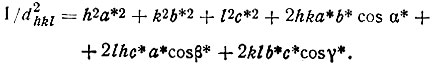(13)

Далее требуется выразить параметры обратной решетки через параметр кристаллографической, воспользовавшись скалярным представлением соотношений (5) и (6)^*. В частности, в случае ортогональной решетки (α= β= γ=90° и соответственно α*= β*= γ*=90°) мы имеем просто a*= 1/а, b*=1/b, с*=1/c и соотношение (13) упрощается до

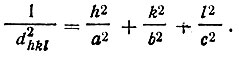
^* (См.: Бокий Г. Б., Порай-Кошиц М. А. Рентгеноструктурный анализ. Т. I. Изд-во МГУ, 1964. С. 316-317.)