Б. Пространственные группы симметрии

§ 4. Обозначения элементов симметрии конечных фигур, принятые в структурной кристаллографии

В фигурах и телах конечных размеров симметрия проявляется в том, что равные части фигуры могут быть совмещены друг с другом либо путем поворота всей фигуры в делом, либо зеркальным отражением в плоскости, пересекающей фигуру, либо одновременным проведением обеих этих операций - поворота и отражения в плоскости, перпендикулярной оси поворота. В частности, поворот на 180°, сопровождаемый отражением, приводит к инверсии фигуры. Обычно именно эти операции и соответствующие им геометрические образы - элементы симметрии - и берутся за основу при описании групп симметрии конечных фигур. Хорошо известны и их обозначения: поворотные оси С_n (n - порядок оси), зеркальное отражение C_s, зеркально-поворотные оси S_n и центр инверсии S₂ или С_i^*.

^* (Заметим, что понятие элемента симметрии соответствует не одной, а ряду операций симметрии, производных от одной из них. Так, например, поворотная ось С₃ содержит представление о самосовмещении фигуры при поворотах как на 120, так и на 240 и 360°.)

Можно, однако, взять за основу не повороты, зеркальные отражения и повороты, сопровождаемые отражением, а несколько иную исходную систему: повороты, инверсию и повороты, сопровождаемые инверсией.

В этом случае зеркальное отражение может рассматриваться как поворот на 180°, совмещенный с инверсией, а зеркальные повороты по определенным правилам, относящимся к порядку оси поворота, сводятся к инверсионным поворотам. В структурной кристаллографии принята именно эта втекая система опорных операций симметрии; на ней основана номенклатура групп симметрии, характеризующих атомную структуру кристаллов. Применяется и совсем иной способ обозначения элементов симметрий; поворотные оси обозначаются цифрами 1, 2, 3..., отвечающими порядку оси, инверсионные оси обозначаются теми же цифрами с чертой 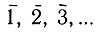В частности , 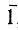- означает центр инверсии. Для плоскостей зеркального отражения принято обозначение m (хотя в принципе можно использовать и 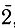). Соотношение между двумя системами и способами обозначений выглядит очень просто:

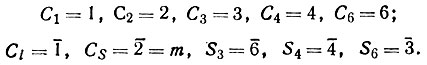
Само понятие симметрии наиболее просто и без внутренних противоречий можно ввести следующим образом.

Нам известны только три действия, которые не изменяют взаимное расположение всех точек любой произвольно выбранной фигуры (тела): это перемещение фигуры как целого, ее инверсия (отражения в точке) и зеркальное отражение. Но, как было сказано, зеркальное отражение может быть сведено к комбинации из перемещения и инверсии. Поэтому можно ограничиться лишь двумя действиями - движением и инверсией как единственными простыми операциями, сохраняющими взаимное расположение (расстояния, углы и т. д.) всех точек любой фигуры. Эта констатация и служит основой для введения понятия симметрии.

Фигуру называют симметричной, если в результате определенного движения, инверсии или совместного проведения этих двух действий все ее точки совпадут с точками, характеризующими первоначальное положение фигуры. Действия, приводящие к самосовмещению фигуры, называют операциями симметрии^*.

^* (Если фигура совмещается со своим первоначальным положением только при повороте на 360° или после совершения полного колебания, то ее можно считать асимметричной или тривиально симметричной. Такой симметрией обладает любое тело. В теории групп симметрии соответствующая операция считается единичной операцией симметрии.)