§ 14. Правильные системы точек

Пространственная группа лишь правило, по которому в материальные частицы - атомы или ионы. Задача рентгеноструктурного исследования состоит в том, что-бы найти само размещение частиц, их координаты. В этом разделе кратко рассматриваются некоторые понятия и термины, связанные с размещением частиц (точек), размножаемых операциями симметрии.

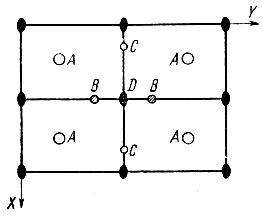
Рис. 21. Общая и частные позиции в пространственной группе Pmm2

Совокупность всех точек, получаемых из исходной всеми операциями симметрии пространственной группы, называется правильной системой точек; местонахождение исходной точки - ее позицией, а число точек системы, приходящихся на одну элементарную ячейку, - кратностью позиции.

Если точка не находится ни на одном из закрытых элементов симметрии, ее позицию называют общей. Такая позиция характеризуется тремя переменными параметрами: х, y, z. Если точка находится на одном из закрытых элементов симметрии или на их пересечении, ее позицию называют частной.

Частная позиция на плоскости зеркального отражения характеризуется двумя параметрами: позиция на поворотной оси любого порядка, начиная с 2, или инверсионной оси любого порядка, начиная с 3, характеризуется одним параметром; позиция в центре инверсии, в точке инверсии инверсионной оси или на пересечении элементов симметрии без параметрическая.

Кратность частной позиции всегда меньше (в целое число раз), чем кратность общей позиции. На рис. 21 в качестве примера приведена пространственная группа Рmm2. Общая позиция А здесь четырехкратная, позиции на плоскостях симметрии (В и С) -двукратные, на осях симметрии (позиция D)-однократные. Понижение кратности позиции при уменьшении числа варьируемых параметров можно рассматривать как результат слияния точек при перемещении их на элемент симметрии.

Каждая позиция характеризуется определенной собственной симметрией. Общая позиция всегда асимметрична. Частные позиции В и С на рис. 21 имеют симметрию m, позиция D - симметрию mm2.