§ 2. Параметры рентгеновских волн; рассеяние рентгеновских лучей

Любая электромагнитная волна задается четырьмя общими параметрами: направлением S, длиной волны λ, амплитудой Е₀, начальной фазой γ (рис. 22). Интенсивность луча пропорциональна квадрату его амплитуды: I∼Е²₀. Все эти параметры используются в ходе анализа структуры.

Рассеяние рентгеновских волн в рамках классической электродинамики описывается как двойной процесс:

а) заряженная частица вещества под действием переменного поля Е приходит в колебательное движение в соответствии с законом механики

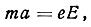(14)

где m - масса частицы; e - ее заряд; a - ускорение;

б) колебательное движение заряда является источником вторичных электромагнитных волн, распространяющихся во всех направлениях. Напряженность поля этих волн в соответствии с общим законом электродинамики определяется соотношением

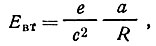(51)

где c - скорость света; R - расстояние от колеблющейся частицы.

Подставляя (14) в (15), имеем

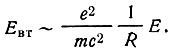
Это означает, в частности, что интенсивность рассеянных волн обратно пропорциональна m². Именно поэтому рассеяние рентгеновских волн определяется электронами, а не ядрами атомов.

Впрочем, приведенная формула требует некоторого уточнения. Она справедлива лишь для случая, изображенного на рис. 23, а: рассматривается рассеяние под углом φ в направлении, перпендикулярном вектору напряженности первичной волны Е, а следовательно, и вектору ускорения заряженной частицы а.

На рис. 23, б представлен другой предельный случай - рассеяние под тем же углом φ в том же направлении, но при условии, что вектор Е, а следовательно, и а лежат в плоскости рассеяния. В этом случае напряженность поперечного поля вторичной волны Е_вт определяется не полной величиной вектора а, а лишь его составляющей, перпендикулярной направлению рассеяния, т. е. величиной a cos φ. Следовательно, теперь

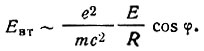
В общем случае, когда напряженность поля Е первичной волны не поляризована в какой-либо определенной плоскости, требуется произвести усреднение по всем возможным ориентациям вектора Е, а следовательно, и а. Это усреднение дает:

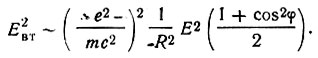(16)

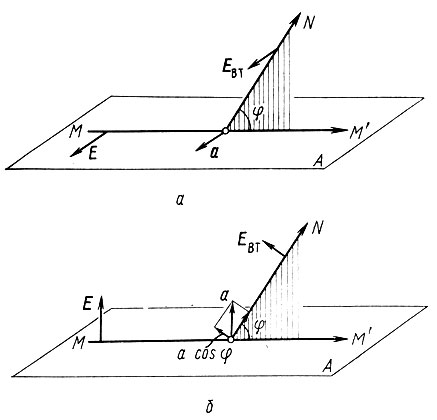
Рис. 23. Зависимость амплитуды рассеяния Е_вт от угла рассеяния: а- вектор напряженности поля первичного пучка Е лежит в плоскости А: б - тот же вектор лежит в плоскости, перпендикулярной А