§ 3. Задачи, решаемые в ходе рентгеноструктурного анализа кристаллов

При исследовании структуры кристалла возникают три задачи : 1) найти размеры и форму элементарной ячейки решетки кристалла (а следовательно, и число атомов, приходящееся на каждую ячейку); 2) определить закон симметрии, по которому атомы должны размещаться в ячейке, т. е. пространственную группу симметрии кристалла; 3) найти конкретное положение (ко-ординаты) каждого симметрически независимого атома ячейки^*.

^* (Здесь перечислены лишь задачи, решаемые в процессе расшифровки структуры. Целью исследования помимо определения координат атомов может быть также установление констант их тепловых колебаний и распределения электронной плотности по атомам и между ними (см. гл. V). )

Рассмотрим на одномерной модели принципиальную связь между характеристиками дифрагированных кристаллом рентгеновских лучей и параметрами структуры.

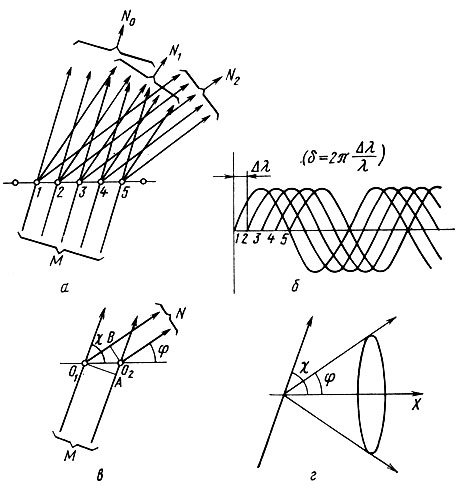
Рис. 24. Рассеяние рентгеновских лучей атомным рядом

На рис. 24, а изображен ряд одинаковых равноотстоящих (точечных) атомов. На него направлен пучок монохроматических рентгеновских лучей. Рассмотрим суммарный эффект рассеяния лучей атомами в разных направлениях. Вдоль направления, продолжающего первичный пучок N₀, путь от источника в точку наблюдения через любой атом одинаков; лучи, рассеянные атомами, совпадают по фазе. Лучи, рассеянные атомами в других направлениях (N₁, N₂ и т. д.), проходят различный путь и поэтому не совпадают по фазе. Если разность фаз лучей, рассеянных соседними атомами, в некотором направлении N_i составляет δ (рис. 24, б), то луч, рассеянный в том же направлении каждым последующим атомом, отличается дополнительным сдвигом по фазе на δ, 2 δ, 3 δ и т. д., и если ряд практически бесконечен (в миллиметровом кристалле более миллиона атомов в каждом направлении!), то для любого рассеянного луча найдется второй с противоположной фазой, и все они взаимно погасят друг друга. Но если δ - разность фаз лучей, рассеянных соседними атомами,- достигает 2 π (или в общем случае р2 π, где р - целое число), то лучи, рассеянные соседними атомами, а следовательно, и всеми остальными атомами ряда, снова совпадут по фазе и взаимно усилят друг друга. Возникает дифракционный луч. Его направление определяется условием, очевидным из рис. 24, в.

Разность пути лучей от источника М в точку наблюдения N через соседние атомы составляет ВО₁-АO₁. Но BO₁= acos φ,AO₂=a cos x. Следовательно, условие дифракции:

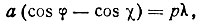(17)

где р= 0, 1, 2, ...^*.

^* ( Верхний предел числа р определяется требованием, чтобы cos φ и cos х оставались в пределах ±1, т. е. чтобы pλ/a≤2. Поэтому, в частности, длина волны вообще должна быть меньше 2а. )

Это условие определяет направления дифракционных лучей (углы φ_p) при заданной периодичности a, длине волны λ и заданном угле x между линией ряда и направлением первичного пучка.

Амплитуда любого дифракционного луча в этом при-мере составляет QE₀, где Е₀ - амплитуда волны, рассеянной одним атомом; Q - общее число атомов в модели.

Теперь представим, что наш ряд состоит из атомов двух сортов (рис. 25, а) (периодичность остается той же). Повторяя ход рассуждения применительно к атомам каждого из сортов в отдельности, получим то же условие (17). Направления дифракционных лучей останутся, следовательно, теми же. Но их интенсивность существенно изменится. Лучи, рассеянные атомом первого сорта O₁ и атомом второго сорта А₁ сдвинуты по фазе на δ, где δ пропорционально расстоянию между атомами. Если расстоянию а отвечает разность фаз 2 πр, расстоянию x должна соответствовать разность фаз δ=2πр(х/а). То же относится к паре 0₂ - A₂, O₃ - A₃ и т. д. В целом каждый дифракционный луч представляет собой наложение двух лучей, во-первых, имеющих разную амплитуду, поскольку мы имеем дело с атомами двух разных сортов, обладающих разной рассеивающей способностью, и, во-вторых, смещенных относительно

друг друга по фазе на δ (рис. 25, б). Поэтому и амплитуда, и начальная фаза результирующей волны зависят от относительной удаленности атомов х/а оба эти параметра, кроме того, различны для разных дифракционных лучей (разных р). В целом амплитуда Е_рез и начальная фаза δ_рез являются функциями атомных номеров элементов Z₁ и Z₂, относительного расстояния между атомами х/а и номера дифракционного луча р:

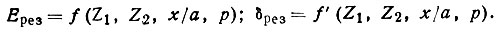
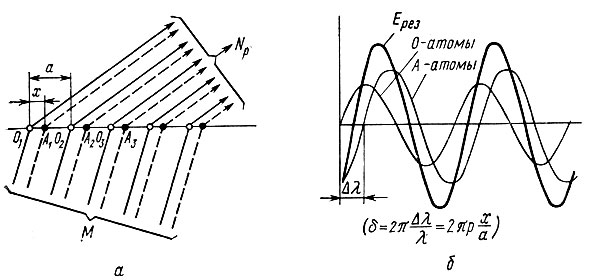
Рис. 25. Дифракция рентгеновских лучей атомным рядом, составленным из атомов двух сортов

Таким образом, направления дифракционных лучей однозначно определяются периодичностью атомного ряда (параметром а), а их интенсивность зависит от индивидуальности и взаимного расположения атомов разного сорта.

В соответствии с этим структурное исследование можно разбить на два основных этапа: 1) определение периодичности (размеров элементарной ячейки кристалла) из анализа геометрии дифракционной картины; 2) определение относительных координат атомов в ячейке из анализа интенсивности дифракционных лучей.

Определение пространственной группы можно считать второй, дополнительной задачей первого этапа.