§ 4. Условия Лауэ

Перейдем от одномерной модели к трехмерной. Так как интенсивность лучей пока не учитывается, будем рассматривать решетчатую модель из атомов одного сорта.

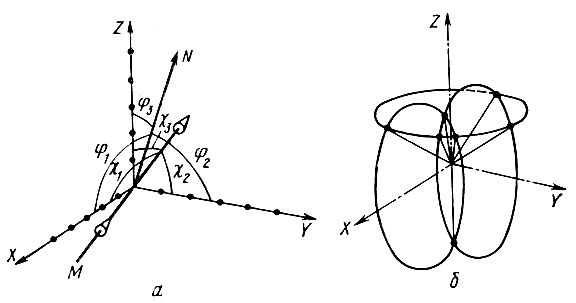
Рис. 26. Дифракция трехмерной системой атомов: а - угловые характеристики первичного и дифракционного лучей; б - интерференционные конусы

Выделим в решетке три ряда атомов, расположенных на координатных осях X, Y и Z (рис. 26, а). Пусть x₁, x₂ и х₃ - углы, образуемые с этими рядами падающим лучом; φ₁, φ₂ и φ₃ - аналогичные углы, образуемые одним из дифракционных лучей.

Как и в предыдущих случаях, лучи не гасятся лишь в таких направлениях, в которых волны, рассеянные всеми атомами, совпадают по фазе или отличаются на целое число периодов. Должны, следовательно, одновременно удовлетворяться три условия:

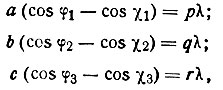(18)

где а, b, с - периоды повторяемости вдоль осей X, Y и Z^*, а р, q, r - целые числа.

^* (Первое условие относится и к ряду, расположенному вдоль оси X, и к любому ряду, параллельному ему. Аналогичное утверждение справедливо в отношении второго и третьего условий. )

Эти условия были найдены Лауэ в 1912 г. и носят его имя.

По своему физическому смыслу целое число р (или, соответственно, q и r) равно разности хода лучей (выраженных в длинах волн), рассеиваемых в дифракционном направлении соседними атомами, расположенными на оси X (или, соответственно, Y и Z). Вместе три числа р, q, r характеризуют одно из дифракционных направлений и называются индексами дифракционного луча. Каждый дифракционный луч характеризуется своей тройкой индексов pqr.

Теперь следует обратить внимание на одну важную деталь. Три направляющих угла любой прямой в пространстве (в нашем случае x₁, x₂ и x₃ или φ₁, φ₂ и φ₃) не являются независимыми. Например, в любой ортогональной системе координат

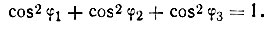(19)

Это означает, что в сущности мы имеем дело с системой, состоящей из четырех уравнений, из которой требуется найти три параметра дифракционного луча. В общем случае такая система не совместна, т. е. направлений, удовлетворяющих условиям дифракции, не существует.

Поясним это более наглядно. Каждое условие Лауэ в отдельности определяет собой конус, образующие которого направлены под углом φ к соответствующей координатной оси (см. рис. 24, г). Два таких конуса, например ориентированные по осям X и Y, пересекаясь, выделяют пару направлений, удовлетворяющих двум из трех условий Лауэ (с целыми числами р и q) (рис. 26, б). Однако третий конус, ориентированный вдоль оси Z, вообще говоря, не обязан пересекаться с остальными по тем же прямым, что и означает несовместимость трех уравнений.

Для создания такой совместимости требуется ввести еще один параметр, варьированием которого можно было бы изменить раствор конуса, а следовательно, создать условия, при которых все три конуса пересекались бы по одному общему направлению. Роль четвертого переменного параметра в принципе может играть либо длина волны рентгеновских лучей, либо поворот кристалла относительно первичного пучка.

Действительно, в условия (18) в качестве параметра входит длина волны λ. Изменение этого параметра означает и изменение углов полу

раствора φ₁, φ₂, φ₃ всех трех конусов. Например, на рис. 26, б достаточно несколько уменьшить эти углы (увеличив λ), и все три конуса пересекутся по общему направлению. Это и будет дифракционный луч с индексами pqr. Аналогичным образом на значение углов φ₁, φ₂, φ₃ влияет и изменение углов (всех трех или только двух) x₁, x₂, x₃ т. е. ориентации кристалла относительно первичного пучка лучей.

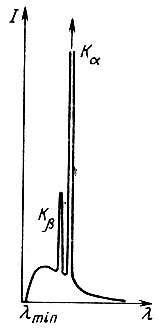
Рис. 27. Белый (непрерывный) и характеристический (К_α^- и K_β -линии) спектры рентгеновского излучения