Определение точечной группы. Закон центросимметричности рентгеновской оптики

По Брэггу, каждый дифракционный луч можно рассматривать как отражение от одной из серий узловых сеток. Поэтому симметрия расположения таких сеток в кристалле должна непосредственно отражаться на симметрии размещения рефлексов на рентгенограммах.

Взаимная ориентация симметрически связанных узловых сеток не зависит от того, включает ли соответствующая операция симметрии трансляционный перенос. В этом смысле узловые сетки нечувствительны к замене операции зеркального отражения на операцию скользящего отражения или простого поворота на аналогичный винтовой поворот. Поэтому по симметрии рентгенограмм можно судить лишь о точечной, но не пространственной группе симметрии кристалла.

Кроме того, возникает еще одно весьма существенное ограничение. Дифракционные лучи с индексами pqr и 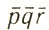по физическому смыслу представляют собой отражения от одной и той же серии плоскостей, но с противоположных сторон (рис. 36). Естественно, что их направления определяются одним и тем же уравнением Брэгга (одно и то же d_hkl), и углы θ_pqr и θ 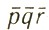- оказываются одинаковыми. Ниже будет показано, что и интенсивности лучей l_pqr и l 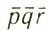- также всегда одинаковы^*.

^* (Это правило нарушается, если, некоторые из атомов, входящих в состав кристалла, попадают в область аномального рассеяния излучения (см. гл.IV, конец § 2))

Сказанное означает, что дифракционная картина, даваемая любым кристаллом, всегда центросимметрична, независимо от того, содержится ли в действительности операция инверсии в точечной группе симметрии кристалла. Это общее правило называется законом центросимметричности рентгеновской оптики (закон Фриделя).

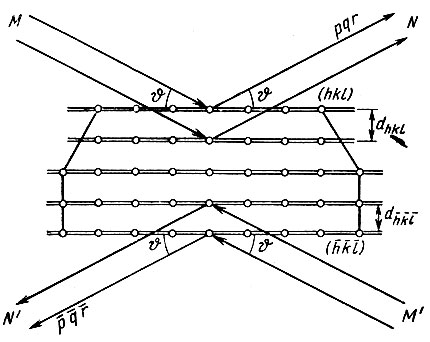
Рис. 36. Иллюстрация закона центросимметричности дифракционного эффекта

Таким образом, точечная группа определяется по симметрии рентгенограмм лишь с точностью до центра инверсии (и равнодействующих элементов симметрии). Например, кристаллы с симметрией 2, m и 2/m дадут рентгенограммы с одинаковой симметрией 2/m. Из 32 кристаллографических групп 11 содержат операцию инверсии. Следовательно, рентгенографически (по симметрии рентгенограмм) все точечные группы распределяются по 11 семействам - так называемым классам Лауэ^*.

^* (Закон Фриделя можно рассматривать как частный случай принципа Неймана; всякое физическое явление обладает определенной собственной симметрией, которая накладывается ("умножается") на симметрию кристалла. В данном случае собственная симметрия рентгеновской оптики - операция инверсии.)