Определение пространственной группы симметрии. Правила погасания

В табл. 3 были приведены правила, определяющие значения индексов h, k и l в символах серий узловых сеток в решетках разного типа: в примитивной решетке h, k, l - целые числа, не имеющие общего множителя; в не примитивных решетках соблюдаются дополнительные правила кратности. Поскольку порядок отражения n может быть любым целым числом, а дифракционные индексы р, q, r равны соответственна nh, nk и nl, то правила, установленные для h, k, l, легко преобразуются в правила, действующие в отношении индексов p, q, r. Эти правила приведены в последнем столбце табл. 3.

В литературе по рентгеноструктурному анализу дифракционные индексы принято обозначать теми же буквами h, k, l, что и индексы серий плоскостей. Поэтому в табл. 3 и далее в тексте обозначения pqr заменены на hkl [символ дифракционного луча hkl записывается без скобок в отличие от символа узловых сеток (hkl)].

Физический смысл правил, приведенных в табл. 3, поясняют рис. 15, а и б, изображающие две решетки с одинаковыми параметрами а, b, с; одна из них примитивная; вторая - С-центрированная. Проведем в первой серию сеток (210) и установим кристалл так, чтобы он давал отражение первого порядка от этой серии, т. е. чтобы 2d₂₁₀sinθ=1λ. Это означает, что лучи, отраженные соседними плоскостями, имеют разность хода в одну длину волны.

Установим С-центрированный кристалл в то же положение. Поскольку аналогичные плоскости проходят в этой решетке вдвое гуще^*, при такой ориентации кристалла разность хода лучей, отраженных соседними плоскостями, составит только половину длины волны, т. е. эти лучи будут иметь противоположные фазы и взаимно погасят друг друга. То же, естественно, произойдет при ориентации, отвечающей отражению любого другого нечетного порядка от плоскостей (210). В С-центрированной решетке соответствующие лучи оказываются "погашенными". Таким образом, сформулированные выше ограничения в значениях индексов hkl можно интерпретировать как правила погасания (точнее, правила не погасания) лучей, дифрагированных решетками, имеющими дополнительные (центрирующие) трансляции.

^* (Их индексы уже не (210), а (420).)

Аналогичное действие - погасание части дифракционных лучей - вызывают также те операции симметрии, которые содержат перенос в качестве одной из компонент операции. Имеются в виду скользящее отражение и винтовое вращение. Однако если понятие центрировки относится к решетке в целом, то понятие скользящего отражения относится лишь к определенной плоскости, а винтового вращения - к определенному направлению. Соответственно этому они вызывают погасания не среди отражений hkl общего типа, а лишь среди отражений определенного частного типа. Так, плоскости скользящего отражения, параллельные координатным плоскостям XY, XZ или YZ, вызывают погасания лишь среди соответствующих "зональных" отражений: hk0, h0l и 0kl, а винтовые оси, параллельные координатным осям X, Y или Z, - лишь среди отражений типа h00, 0k0 и 00l соответственно. Сам характер погасаний зависит от направления и величины трансляционного переноса. Так, например, плоскость скользящего отражения, параллельная плоскости XY, с переносом, равным 1/2 полной трансляции (рис. 37), вызывает погасания среди отражений hk0 по следующим правилам.

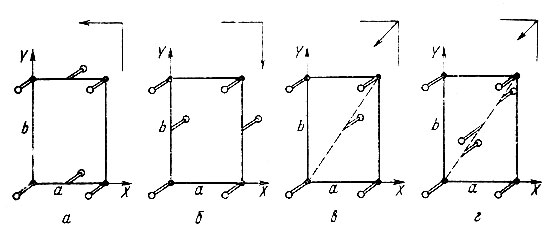
Рис. 37. Скользящие отражения, приводящие к погасаниям среди отражений типа hk0

Если скольжение направлено вдоль оси X (α -скольжение), сохраняются отражения hk0 лишь с h=2n (рис. 37, а); если скольжение направлено вдоль оси Y (b- скольжение), сохраняются hk0 с k=2n (рис. 37, б); если скольжение направлено вдоль диагонали XY (n- скольжение), сохраняются hk0 лишь с h+k=2n (рис.37, б)^*. Если в последнем случае величина скольжения равна не а трансляции (d-скольжение), то сохраняются лишь отражения с h+k=4n (рис. 37, г). Правила погасаний для плоскостей скользящего отражения, параллельных другим координатным плоскостям, естественно, аналогичны с соответствующей перестановкой индексов.

^* (Легко проследить аналогию между случаем n-скольжения в плоскости XY (рис. 37, в) и С-центрированностью решетки. В проекции на плоскость XY атомы, связанные скользящим отражением, образуют мотив, центрированный по грани ячейки ab. Естественно, что они вызывают погасания по аналогичному правилу h + k= 2п, но лишь среди отражений hk0, коль скоро речь идет только о проекции на плоскость XY. Это сопоставление позволяет понять, почему плоскости скользящего отражения вызывают погасания только среди отражений зонального типа (с одним нулевым индексом).)

Характер погасаний, вызываемых присутствием винтовой оси, также зависит от величины переноса вдоль оси вращения. Пусть ось n-ного порядка параллельна оси Z. При переносе, равном 1/2, 1/3, 1/4, 1/6 трансляции с, присутствуют отражения 00l лишь с l=2n, 3n, 4n 6n соответственно.

Правила погасаний дают сведения о центрированности решетки и о присутствии плоскостей скользящего отражения и винтовых осей. При отсутствии регулярных погасаний сохраняется известная неопределенность: остается неясным, заменяется ли в рамках данного класса Лауэ скользящее отражение на зеркальное, а винтовой поворот на простой поворот, или таких операций вообще в кристалле нет.

Если, например, в классе Лауэ 2/m (точечные группы 2, m или 2/m) среди отражений hkl погасаний нет, среди hk0 присутствуют лишь отражения с h=2n, а среди 00l - лишь с l=2n, то пространственная группа определяется однозначно как Р2₁/a (примитивная решетка, плоскость скольжения, винтовая ось). Но если срабатывает только правило: среди hk0h=2n, - то возможны как Р2/а, так и Ра. Аналогично, если действует только правило: среди 00l1=2n, - то возможны группы Р2,sub>1/m или Р2₁. И, наконец, если нет никаких регулярных погасаний, то возможны три группы: Р2/m, Рm и Р2.

С учетом симметрии рентгенограмм возможны всего 122 различные комбинации правил погасания. Их называют дифракционными группами. В 61 из них пространственная группа определяется однозначно^*, в остальных с точностью до двух-четырех возможных групп.

^* (Включая сюда и энантиоморфные пары. )

Дополнительные возможности для уточнения пространственной группы дает систематический анализ интенсивности дифракционных лучей. Суть дела в следующем. Понятно, что интенсивность любого дифракционного луча зависит от структуры кристалла и в принципе индивидуальна для каждого вещества. Однако статистическое распределение дифракционных лучей по их интенсивности, т. е. относительное количество дифракционных лучей ΔN/N_общ с интенсивностью в заданном интервале ΔI/I_max, подчиняется некоторым общим закономерностям, которые не зависят от индивидуальности исследуемого вещества, но определяются его симметрией. В частности, это распределение различно для центросимметричных и не центросимметричных кристаллов. Поэтому, анализируя статистическое распределение по интенсивности лучей, дифрагированных исследуемым кристаллом, можно судить, содержит ли его пространственная группа центры инверсии. К сожалению, этот критерий срабатывает не во всех случаях, так как разница в распределении отражений по интенсивности у центросимметричных кристаллов не столь уж велика.

Если пространственная группа определяется неоднозначно, дальнейшее структурное исследование приходится проводить, учитывая варианты, основанные на каждой из возможных групп симметрии.