
§ 7. Метод межатомной функции
Понятие о межатомной функции
В поисках метода, позволяющего исключить начальные фазы из соотношений, связывающих дифракционные данные со структурными параметрами, Паттерсон предложил воспользоваться математической функцией, известной под названием самосвертки*, т. е. интегралом типа
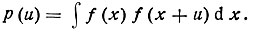 (44)
(44)В данном случае роль обрабатываемой функции выполняет электронная плотность. Под интегралом находится произведение электронных плотностей в двух точках ячейки r и r+u, разделенных вектором u. Интегрирование производится по всей ячейке, т. е. при перемещении вектора u параллельно самому себе, так что его "начало" располагается последовательно во всех точках ячейки:
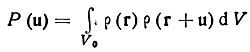
или
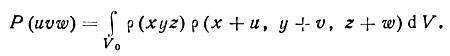 (45)
(45)Результат, естественно, зависит от выбранного вектора u.
* (См.: Китайгородский А. И. Теория структурного анализа.- М., Изд-во АН СССР, 1957. С. 20.)
Функция Р(u) называется межатомной или паттерсоновской*.
* (Идея А.Л. Панттесона, опубликованная в 1935 г., представляла собой естественное развитие метода радиального распределения, разработанного на год раньше Б.Е. Уорреном применительно к жидкостям и стеклам)
Какие возможности открывает введение этой функции?
- Расчет функции Паттерсона не требует знания начальных фаз отражений.
Действительно, представим p(xyz) и p(x+u, y+v, z+ω) в виде рядов Фурье по (35):
Интегралы от периодических функций типа
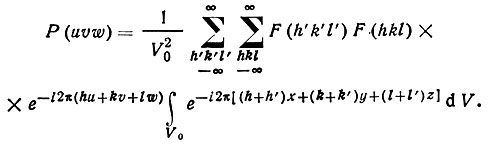 по величине полного периода отличны от нуля только при условии, что целое число n равно нулю" т. е. в данном случае при условии, что h' =-h, k' = -k, l'=l. При соблюдении этого условия результат интегрирования равен V0. С другой стороны
по величине полного периода отличны от нуля только при условии, что целое число n равно нулю" т. е. в данном случае при условии, что h' =-h, k' = -k, l'=l. При соблюдении этого условия результат интегрирования равен V0. С другой стороны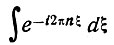
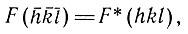 (см. гл. IV, § 2) и, следовательно, F(
(см. гл. IV, § 2) и, следовательно, F(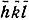 )F*(hkl)=|F(hkl)|2. В результате получим
Поскольку |F(hkl)|2 - вещественные величины, |F(hkl)|2=|F(
)F*(hkl)=|F(hkl)|2. В результате получим
Поскольку |F(hkl)|2 - вещественные величины, |F(hkl)|2=|F(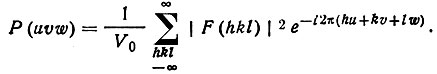 (46)
(46)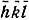 )|2, а суммирование ведется от- ∞до + ∞, то последнюю формулу можно также написать в виде*
*Если
)|2, а суммирование ведется от- ∞до + ∞, то последнюю формулу можно также написать в виде*
*Если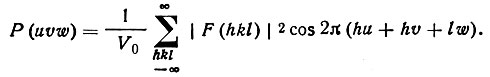 (47)Правая часть - ряд Фурье, похожий на тот, которым определялась электронная плотность, но содержащий в качестве коэффициента не F(hkl), a |F(hkl)|2. Начальные фазы в полученный ряд не входят. Паттерсоновская функция зависит только от значений |F(hkl)|2эксп∼Iэксп и, следовательно, может быть рассчитана по экспериментальным данным (для любого вектора u).
(47)Правая часть - ряд Фурье, похожий на тот, которым определялась электронная плотность, но содержащий в качестве коэффициента не F(hkl), a |F(hkl)|2. Начальные фазы в полученный ряд не входят. Паттерсоновская функция зависит только от значений |F(hkl)|2эксп∼Iэксп и, следовательно, может быть рассчитана по экспериментальным данным (для любого вектора u).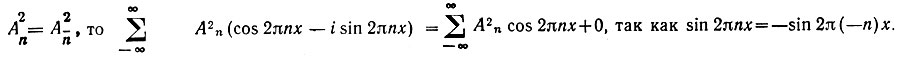
- Расчет функции Паттерсона позволяет выявить систему межатомных векторов в исследуемой структуре.
Рассмотрим предельный случай структуры, построенной из точечных атомов. На рис. 42, а изображена некоторая гипотетическая структура. Возьмем некоторый произвольный вектор u и рассчитаем Р(u). Результат будет равен нулю, поскольку при интегрировании (при перемещении вектора по ячейке) либо один, либо оба конца вектора будут находиться в точке с нулевой электронной плотностью. Функция Р(u) окажется отличной от нуля лишь в том случае, когда вектор u при перемещении соединит два атома структуры, т. е. если он будет межатомным вектором.
При таком условии
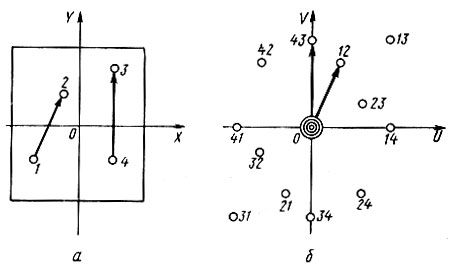
Рис. 42. Модельная структура из четырех атомов на ячейку (а) и соответствующая ей векторная система (б)Сказанное относится к межатомным векторам, связывающим любые пары атомов i и j структуры. Иначе говоря,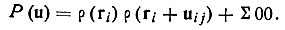 где ri - радиус-вектор i-го атома; uij - межатомный вектор, связывающий i-й и j-й атомы. Паттерсоновскую функцию Р(u) в общем случае можно представить как функцию типа "плотности", распределенную в некотором трехмерном пространстве, где роль координат играют компоненты вектора и, т. е. u, u и ω. ЕСЛИ структура построена из точечных атомов, то и в этом "паттероновском" пространстве выделятся лишь дискретные точки, расположенные в вершинах веера всех межатомных векторов, отложенных от общего начала координат (рис. 42, б). Поскольку в кристаллах центры тяжести атомов расположены на достаточно больших расстояниях друг от друга [максимумы р(r) хорошо разделяются], переход от точечных атомов к реальным не вызывает качественного изменения общей картины. Функция Р(u) становится, конечно, непрерывной. Но основное ее свойство остается неизменным: максимумы "плотности" Р(u) паттерсоновского пространства располагаются в концах векторов uij, отложенных от общего начала координат.
где ri - радиус-вектор i-го атома; uij - межатомный вектор, связывающий i-й и j-й атомы. Паттерсоновскую функцию Р(u) в общем случае можно представить как функцию типа "плотности", распределенную в некотором трехмерном пространстве, где роль координат играют компоненты вектора и, т. е. u, u и ω. ЕСЛИ структура построена из точечных атомов, то и в этом "паттероновском" пространстве выделятся лишь дискретные точки, расположенные в вершинах веера всех межатомных векторов, отложенных от общего начала координат (рис. 42, б). Поскольку в кристаллах центры тяжести атомов расположены на достаточно больших расстояниях друг от друга [максимумы р(r) хорошо разделяются], переход от точечных атомов к реальным не вызывает качественного изменения общей картины. Функция Р(u) становится, конечно, непрерывной. Но основное ее свойство остается неизменным: максимумы "плотности" Р(u) паттерсоновского пространства располагаются в концах векторов uij, отложенных от общего начала координат.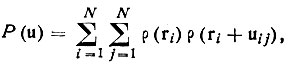 (48)Сказанное означает, что расчет P(uvω) по формуле (47) позволяет в принципе найти систему межатомных векторов, соединяющих атомы исследуемого кристалла.
(48)Сказанное означает, что расчет P(uvω) по формуле (47) позволяет в принципе найти систему межатомных векторов, соединяющих атомы исследуемого кристалла.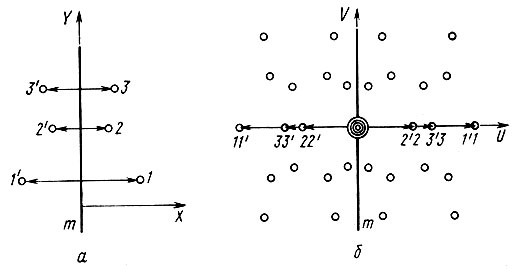
Рис. 43. Модельная структура с плоскостью зеркального отражения (а) и соответствующая ей векторная система (б) - Паттерсоновская функция обладает рядом свойств, существенных для ее использования в процессе анализа структуры:
а) поскольку электронная плотность периодична с периодами a, b и с, аналогичной периодичностью обладает пространство межатомной функции;
б) симметрия структуры отражается (с некоторыми изменениями) в симметрии пространства межатомной функции. Важнейшее изменение заключается в добавлении центра инверсии в начале координат. Это вытекает из рис. 42 (атомы i и j связаны как вектором uij и вектором uji=-uij формулы (45) (возможность замены переменных: t на r-u без изменения резутата) и, наконец, из формулы (46) (косинус - центроримметричная функция). Результат и не мог бы быть иным, поскольку по закону Фриделя дифракционный эффект центросимметричен, а паттерсоновская функция основана только на экспериментальных дифракционных данных;
в) условия симметрии, действующие на атомы в кристалле, приводят к определенным закономерностям в ориентации межатомных векторов, а следовательно, и во взаимном расположении максимумов в паттерсоновском пространстве. Так, например, в присутствии плоскости зеркального отражения все атомы связаны попарно векторами, перпендикулярными этой плоскости (11', 22', 33') (рис. 43, а). Будучи отложены от общего начала координат в паттерсоновском пространстве, эти векторы создают системы максимумов на оси, перпендикулярной плоскости отражения (рис. 43, б). Аналогичным образом поворотные оси симметрии создают максимумы, расположенные в координатной плоскости паттерсоновского пространства, перпендикулярной оси симметрии. Определенные правила размещения максимумов вызываются и другими элементами симметрии. Дополнительные закономерности возникают при сочетании нескольких элементов симметрии. Возьмем, например, кристалл с симметрией Ртт2 (примитивная решетка, две взаимно перпендикулярные плоскости зеркального отражения и ось второго порядка по линии их пересечения). На рис. 44, а показаны четыре атома, связанные этими операциями симметрии; на рис. 44, б - взаимное расположение максимумов, отвечающим векторам, соединяющим эти атомы. Взаимосвязь в координатах и, v, ω этих максимумов ясна из рис. 44, б*; г) если в элементарной ячейке кристалла имеется N атомов, то в аналогичной ячейке пространства межатомной функции их должно быть N (N-1) (каждый атом связан векторами uij с N-1 другими). Правда, некоторые из них могут налагаться друг на друга по условиям симметрии или из-за случайного совпадения векторов uij. Кроме того, каждый атом находится на нулевом расстоянии от самого себя, поэтому в начале координат пространства Р(u) налагается N максимумов; д) мощность максимума межатомной функции пропорциональна произведению мощности максимумов электронной плотности той пары атомов, которую этот максимум отображает. В первом приближении можно считать, что высота максимума Р(uij) пропорциональна ZiZj, где Z - атомный номер; е) можно показать, что максимумы Р(u) имеют более пологие (более размытые) склоны, чем максимумы р(r).
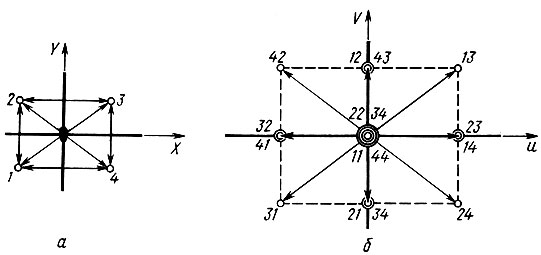
Рис. 44. Симметрически связанные атомы в группе Ртт2 (а) и соответствующее им расположение максимумов в паттерсоновском пространстве (б)
* (Подробнее см.: Порай-Кошиц М. А. Практический курс рентгеноструктурного анализа. М., Изд-во МГУ, 1960. Т. II. С. 439-444.)
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'