§ 6. Общая схема второго этапа анализа структуры

Согласно формуле (28) структурные амплитуды всех отражений зависят от одних и тех же координатных параметров x_j, y_j, z_j . Это означает, что разные F(hkl) как-то связаны между собой. Поскольку F(hkl)=|F(hkl)|e^{i φ(hkl)}, должна существовать и определенная взаимосвязь между амплитудами |F(hkl)\ и начальными фазами φ(hkl) разных отражений.

В структурах средней сложности число независимых координатных параметров не превышает 150-200^*, а общее число дифракционных лучей, даваемых таким кристаллам, достигает нескольких тысяч. Следовательно, число экспериментально определенных |F(hkl)| значительно больше числа неизвестных x_j, y_j, z_j. Это обстоятельство создает возможность либо обойти проблему начальных фаз и определить координаты некоторой части атомов структуры без оценки φ (hkl), либо решить проблему начальных фаз, т. е. определить значения φ (hkl) [в центросимметричном случае S(hkl)] некоторой части отражений. Алгоритмы, позволяющие это сделать, рассматриваются в § 7 и 8 этой главы. Пока же, забегая вперед, допустим, что координаты нескольких атомов уже удалось определить (стрелка 1 на схеме). Обычно это те атомы соединения, которые имеют наибольшие атомные номера и соответственно наибольшие f_j. Такие атомы вносят наибольший вклад в структурные амплитуды согласно формуле (28)^**.

^* (Если порядок точечной группы кристалла равен q, а в элементарной ячейке имеется N атомов, занимающих общие позиции, то симметрически независимых атомов будет n=N/g, а число координатных параметров x_j, y_j, z_j, подлежащих определению в процессе анализа структуры, будет 3n.)

^** (Далее эти атомы будут называться "тяжелыми".)

Используем координаты найденных t атомов и табличные значения их f_j для составления структурных амплитуд в первом, самом грубом приближении (стрелка 2):

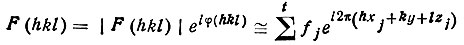
(в суммировании не учитываются все атомы от t+1 до N). Из полученных F(hkl) найдем лишь приближенные значения начальных фаз ∼ φ(hkl) (стрелка 3) и используем их вместе с экспериментальными |F(hkl)|_эксп (стрелки 4 и 5) для расчета обратной зависимости: распределения электронной плотности по дифракционным данным [уравнение (40)]. В полученном распределении обязаны выявиться все максимумы, отвечающие первым атомам, взятым за основу, но должны также проявиться и дополнительные максимумы, соответствующие некоторым другим (более легким) атомам (стрелка 6):

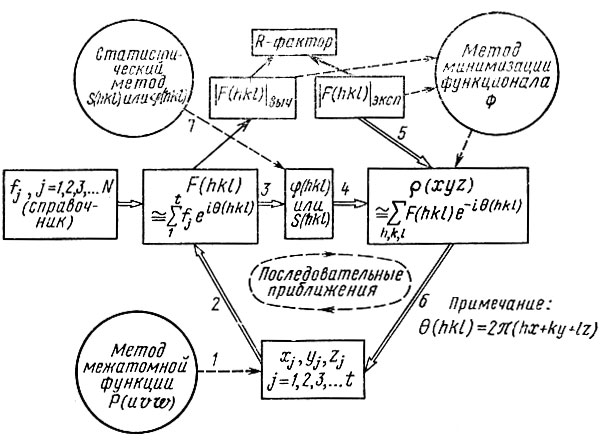
Поскольку при расчете использовались неточные значения φ (hkl), распределение р(х, у, z) не может еще содержать всех деталей. Но обогащение первоначального набора атомов позволяет повторить процедуру еще раз на основе большего числа атомов (см. схему). Процесс последовательных приближений может повторяться несколько раз, пока распределение p(xyz) не выявит всех атомов элементарной ячейки.

В рассмотренной схеме исходным пунктом послужили координаты нескольких наиболее тяжелых атомов элементарной ячейки. Это лишь одна из возможностей. Другим исходным пунктом могут послужить знаки структурных амплитуд (а в не центросимметричном случае грубо оцененные начальные фазы) некоторой части отражений (стрелка 7). Обычно удается определить знаки амплитуд, наибольших по абсолютной величине, т. е. вносящих наибольший вклад в формулу распределения электронной плотности. По этим отражениям, т. е. по их знакам и экспериментальным |F(hkl) |_эксп, и строит-ся распределение электронной плотности первого приближения, начинающее круговой процесс последовательных итераций.

Контролем правильности интерпретации новых деталей распределения плотности, выявляемых на каждом витке процесса последовательных приближений, служит характер распределения р(xyz): в нем должны постепенно исчезать "всплески" фона между максимумами и выявляться разумное размещение атомов. Дополнительным критерием служит постепенное сближение величин |F(hkl) |_выч и значений |F(hkl)|_эксп- Параметром, характеризующим это сближение, является так называемый R-фактор или фактор расходимости:

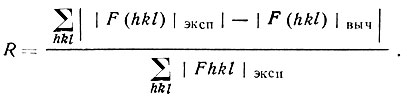(43)

Фактор R должен уменьшаться по мере выявления координат атомов.

После нахождения всех атомов исследование вступает в новую стадию - уточнения координат атомов (и констант их тепловых колебаний), которая проводится на основе метода наименьших квадратов. Уточнение завершается анализом полученных результатов: определением формы координационных полиэдров атомов, межатомных расстояний и валентных углов.

Таким образом, второй этап структурного исследования обычно состоит из четырех стадий: 1) получение опорных данных (координат некоторых атомов или начальных фаз части отражений); 2) установление координат всех атомов в процессе последовательных приближений; 3) их уточнение методом наименьших квадратов; 4) интерпретация результатов.

Вторая стадия была только что описана. Остальные рассматриваются более детально далее. Важнейшей является, естественно, первая стадия - получение опорных данных.

В настоящее время получили наибольшее признание два различных по своей принципиальной основе метода получения опорных данных: 1) метод межатомной функции, или метод Паттерсона, используемый для определения координат опорных атомов; 2) статистический метод (связанный, в первую очередь, с именем В. Г. Захариазена и значительно усовершенствованный Дж. Карлем и Г. Хауптманом), используемый для определения начальных фаз (знаков) опорных отражений.

Так как расшифровка паттерсоновской функции не всегда оказывается вполне однозначной, в первом из этих подходов иногда сохраняются элементы метода проб и ошибок. Поэтому термин "прямой метод" исторически закрепился за вторым подходом к задаче - за статистическим определением начальных фаз или знаков структурных амплитуд.

Помимо этих двух основных методов иногда применяется третий - метод минимизации структурного функционала типа R-фактора, предложенный советским математиком И. М. Гельфандом. Этот метод используется главным образом при анализе тех кристаллических структур, где форма молекулы (или по крайней мере основной ее части) известна заранее.