§ 8. Статистический (прямой) метод определения начальных фаз

Как уже упоминалось, структурные амплитуды разных отражений должны быть как-то связаны друг с другом, поскольку все они зависят от одних и тех же координатных параметров атомов. Это положение можно выразить и нагляднее.

В соответствии с формулой (40)

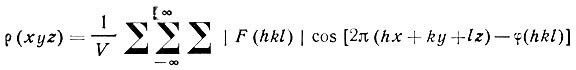
распределение электронной плотности в кристалле можно представить как совокупность плоских косинусоидальных волн плотности, имеющих разную амплитуду | F (hkl)|, разное направление в пространстве и разную периодичность. Направление и периодичность каждой из них определяется аргументом 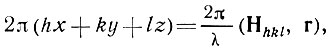т. е. каждая волна плотности hkl ориентирована перпендикулярно серии узловых сеток (hkl) и имеет периодичность, равную d_hkl (рис. 47). Начальная фаза φ (hkl) определяет сдвиг Δ ближайшего гребня волны по отношению к началу координат.

Любая структура должна удовлетворять двум общим условиям: в распределении электронной плотности р(r), во-первых, не должно быть отрицательных значений р, во-вторых, должно присутствовать конечное число приблизительно сферически симметричных максимумов. Выполнение этих требований, естественно, накладывает определенные ограничения как на амплитуды волн плотности |F(hkl) |, так и на их сдвиги φ (hkl). Даже при одном и том же наборе амплитудных значений волн плотности произвольное варьирование их фазовых смещений лишит распределение р(r) физического смысла: неизбежно появятся области р(r)<0 и произойдет размазывание максимумов плотности, отвечающих атомам.

Рис. 47. Волна плотности |F(hkl)|cos[2π(hx+ky+lz)- Φ(hkl)] сдвиг гребня волны определяется отношением Δd_hkl=Φ(hkl):2π (на рисунке показана волна с индексами 230)

Именно на основе двух сформулированных условий в 1952 г. Д. Сейр вывел наиболее общее уравнение, связывающее вместе тройные произведения структурных амплитуд всех отражений, а В. Г. Захариазен сформулировал статистически между знаками структурных амплитуд троек отражений от центросимметричного кристалла и продемонстрировал путь практического применения этого соотношения к анализу структур.

В последующие годы главным образом работами В. Кокрена, М. Вульфсона, А. И. Китайгородского, Дж. Карля и Г. Хауптмана была развита более строгая теория статистических соотношений между структурными амплитудами, охватывающих не только тройки, но и большее число отражений. Последовательное изложение всех аспектов этой теории, включающей несколько разных подходов, потребовало бы введения многих новых понятий и трудоемких математических выкладок, что не-возможно сделать в рамках этой книги^*. Поэтому мы ограничимся анализом только самого простого случая тройных произведений амплитуд и лишь вскользь упомянем о произведениях, охватывающих большее число амплитуд, в частности о четверных произведениях.

^* (Для подробного ознакомления можно рекомендовать сборник под ред. М. Ледда и Р. Палмера "Прямые методы в рентгеновской кристаллографии". М., Мир, 1983)

Автор все же обращает внимание читателя на то, что весь материал, связанный с проблемой прямого определения начальных фаз, требует обращения к концепциям совсем иного плана, чем те, которые рассматривались выше, и поэтому не может быть изложен столь же конспективно и прямолинейно. Учитывая, однако, что в современном РСА прямые методы определения начальных фаз отражений становятся главным инструментом расшифровки структур, представляется целесообразным изложить этот раздел несколько подробнее, чем остальные. В нем будут рассмотрены перечисленные ниже вопросы.

1. Наглядный (но нестрогий) вывод основного фазового соотношения для замкнутой системы из трех (а также четырех) отражений в не центросимметричной структуре и аналогичного соотношения между знаками структурных амплитуд троек отражений в центросимметричном случае.
2. Более строгий вывод того же фазового соотношения для системы из трех отражений на основе общего равенства Сейра.
3. Общие положения статистики тройных (а также четверных) произведений структурных амплитуд, позволяющие оценить вероятность выполнения фазовых соотношений, упомянутых в п. 1.
4. Практические приемы расшифровки структур на основе фазовых соотношений.