
Взаимосвязь между начальными фазами. Фазовые инварианты
Вполне понятно, что начальные фазы отражений зависят от выбора начала координат. Если начало сместить на вектор r0=x0a+y0b+z0c, то радиус-векторы всех атомов элементарной ячейки изменятся на ту же величину и вместо rj=xja+yjb+zjc будут иметь значения r'j=rj-r0. Начальная фаза луча, рассеянного в направлении hkl любым j-м атомом, равная, согласно (26), 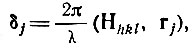
тоже изменится на одну и ту же величину 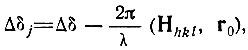 (Hhkl, rj) а значит, на ту же величину изменится и начальная фаза суммарного дифракционного луча hkl:
(Hhkl, rj) а значит, на ту же величину изменится и начальная фаза суммарного дифракционного луча hkl:
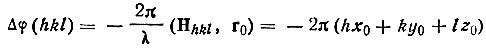
[см. формулу (25)]. Таким образом, смещение начала координат в точку x0y0z0 приводит к изменению начальной фазы каждого дифракционного луча на -2π(hx0+ky0lz0).
Существуют, однако, такие комбинации начальных фаз, которые не зависят от выбора начала координат. Их называют фазовыми инвариантами. К числу таких инвариантов относятся, в частности, суммы начальных фаз 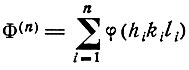 замкнутой системы отражений, т. е. совокупности n отражений, удовлетворяющих условиям h1+h2+…+hn=0,k1+k2+…+kn=0, l1+l2+…ln=0 или, иначе говоря, условию
замкнутой системы отражений, т. е. совокупности n отражений, удовлетворяющих условиям h1+h2+…+hn=0,k1+k2+…+kn=0, l1+l2+…ln=0 или, иначе говоря, условию
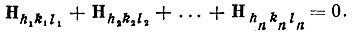 (51)
(51)
Действительно, при переносе начала координат на вектор r0 сумма Φ(n) должна измениться на
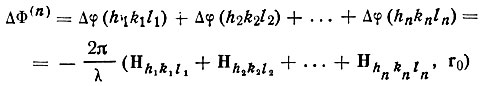
и в силу условия замкнутости системы обратных векторов ΔΦ(n)=0.
Из n взятых отражений п-1 независимы, а индексы n-го определяются условиями (51).
Для краткости введем условные обозначения:
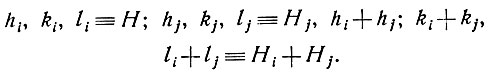
Практически наиболее существенны тройные и четверные варианты:
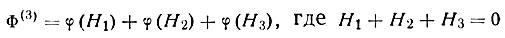
и
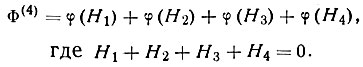
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'