Значения фазовых инвариантов Φ(3) и Φ(4) для сильных отражений

Предположим, что все отражения H₁, H₂ и H₃, входящие в замкнутую совокупность, имеют большие по модулю амплитуды |F(H₁)|, |F(H₂)| и |F(H₃)| (далее такие отражения мы будем называть "сильными"). Вероятнее всего, большие значения амплитуд определяются тем, что какие-то атомы структуры, скорее всего тяжелые, располагаются вблизи общих (или почти общих) точек пересечения волн плотности, отвечающих этим трем отражениям. На рис. 48, а выделены волны h₁k₁l₁ и h₂k₂l₂ гребни изображены сплошными линиями, впадины - пунктирными. Их точки пересечения выделяют максимум плотности А и отрицательные минимумы В. Теперь учтем волну плотности с индексами - (h₁+h₂), -(k₁+k₂), -(l₁+l₂). По своей ориентации она является "диагональной" по отношению к "сетке", создаваемой первыми двумя, и имеет периодичность, согласующуюся с периодичностью диагоналей этой сетки^*.

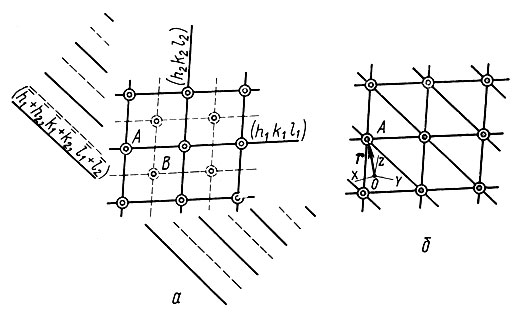
Рис. 48. Схема пересечения гребней и впадин волн плотности, отвечающих замкнутой системе из трех сильных отражений: а - волны плотности; б - волны плотности h₁k₁l₁ и h₂k₂l₂

Если эта волна также отвечает сильному отражению, то и она должна быть сдвинута по фазе так, чтобы гребни проходили через точки пересечения (или вблизи точек пересечения) гребней волн (h₁k₁l₁), (h₂k₂l₂) (рис. 48, б); это не только усилит максимумы A, но и ослабит ложные минимумы в точках В [первое требование к электронной плотности, р(r₀)≥0].

^* (Это положение с очевидностью справедливо для комбинации из серий плоскостей (100), (010) и (110). В обратной решетке вектор H₁₁₀ есть взятая с обратным знаком сумма векторов Н₁₀₀ и Н₀₁₀. Но аналогичным образом и вектор 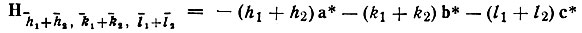, есть сумма векторов H_h1k1l1 и H_h2k2l2 с обратным знаком). Следовательно, и в прямой решетке ситуация с плоскостями (h₁k₁l₁), (h₂k₂l₂) и 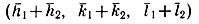должна быть такой же, как с плоскостями (100), (010) и (110): серия плоскостей 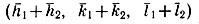должна быть диагональной по отношению к "сетке", выделяемой пересечениями плоскостей (h₁k₁l₁), (h₂k₂l₂) с периодичностью, соответствующей соотношению между длинами векторов.)

Как такое взаимное расположение гребней трех волн скажется на инварианте Φ⁽³⁾?

Пусть ближайшая к началу координат точка пересечения гребней А определяется радиус-вектором r_A с координатами x_A, y_A, z_A. Тогда начальная фаза отражения h₁k₁l₁ может быть представлена как

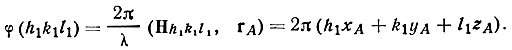
Аналогичный вид имеют и начальные фазы двух других отражений, а следовательно, их сумма равна

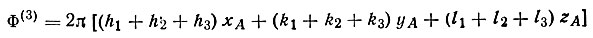
и в силу условия замкнутости трех взятых отражений (H₁+H₂+H₃=0) вся правая часть оказывается равной нулю.

В действительности этот результат является лишь вероятным и лишь приблизительно правильным: большие значения амплитуд всех трех отражений замкнутой системы, вероятно, определяются присутствием (тяжелого) атома вблизи одной из общих точек пересечения гребней трех волн плотности (максимумы в остальных точках пересечения гребней могут быть уничтожены совокупностью волн плотности, отвечающих всем другим отражениям); пересечение трех волн не обязано происходить точно в одной точке, и инвариант Φ⁽³⁾ должен быть лишь близок к нулю (с модулем 2π)^*.

^* (Выражение типа 2π(hx_A+ky_A+lz_A) может оказаться больше 2nπ (n - целое число), и тогда начальную фазу следует писать в виде φ(hkl)=2π(hx_A+ky_A+lz_A)-2πn. Поэтому в общем случае сумма Φ⁽³⁾ равна не нулю, а целому числу 2π или, как обычно говорят, равно нулю с модулем 2π.)

Общий результат коротко формулируется так: для трех сильных отражений замкнутой системы H₁+H₂+H₃=0 инвариант

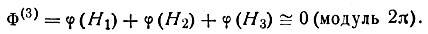(52)

Аналогичным образом можно найти и значение инварианта для замкнутого квартета H₁+H₂+H₃+H₄=0 сильных отражений. На рис. 49, а изображены соседние гребни трех независимых волн плотности h₁k₁l₁, h₂k₂l₂ и h₃k₃l₃. В общих точках их пересечения находятся максимумы А (кружки), посередине между ними - минимумы В (крестики). Серия плоскостей "телесно-диагональная" по отношению к параллелепипедам, выделяемым этими тремя сериями, имеет индексы h₄= -h₁-h₂-h₃, k₄= -k₁-k₂-k₃, l₄= -l₁-l₂-l₃^*. Коль скоро все четыре отражения сильные, вблизи одной или нескольких точек А должны находиться атомы; поэтому вероятно, что волны h₄k₄l₄ будут проходить гребнями через те же точки (рис. 49, б). А это последнее предположение сразу приводит к вероятному результату:

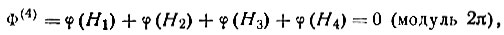(53)

если H₁+H₂+H₃+H₄=0 и все четыре отражения сильные.

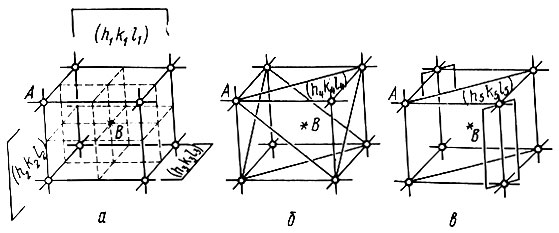
Рис. 49. Схема пересечения гребней и впадин волн плотности, отвечающих замкнутой системе из четырех и семи сильных отражений: а - волны плотности h₁k₁l₁, h₂k₂l₂, h₃k₃l₃; б - дополнение волновой плотности h₄=h₁+ h₂+h₃ , k₄=k₁+k₂+k3, l₄= l₁+l₂+l₃ ; в - дополнение волновой плотности h₅=h₁+h₂, k₅=k₁+k₂, l₅=l₁+l₂

^* (По аналогии с двумерным случаем: плоскости 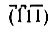являются телесно-диагональными по отношению к (100), (010) и (001). В обратной решетке вектор 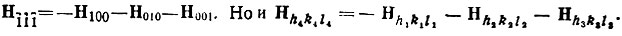. Следовательно, и в прямой решетке серия плоскостей (h₄k₄l₄) телесно-диагональна по отношению к параллелепипедам, выделяемым плоскостям (h₁k₁l₁), (h₂k₂l₂) и (h₃k₃l₃).)

Впрочем значимость (величина вероятности) этого результата ниже, чем в случае тройного инварианта, хотя бы потому, что гребень телесно-диагональной волны не проходит через точки В и, следовательно, не ликвидирует ложных минимумов.

Если, однако, сильными являются еще три отражения с индексами: H₅=-H₁-H₂, H₆=-Н₁-H₃ и Н₇= -Н₂-Н₃, то кроме Φ⁽⁴⁾(H₁H₂H₃H₄)=0 действуют и инварианты Φ⁽³⁾(H₁H₂H₅) =0, Φ⁽³⁾(H₁H₃H₆)=0, Φ⁽³⁾(H₂H₃H₇) =0 (на рис. 49, в показаны гребни волн плотности, отвечающих отражению H₅ с индексами h₅=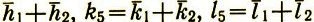) В этом случае минимумы В ликвидируются.