Определение параметров волновых функций

Рассмотренные выше примеры демонстрируют возможности РСА как вспомогательного средства решения квантовохимических задач. В более общем виде взаимосвязь между рентгеноструктурным анализом и квантовой химией устанавливается через соотношение

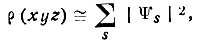(93)

где Ψ_s - волновые функции всех МО системы, заполненных электронами.

При решении уравнения Шредингера для системы любым из существующих приближенных методов приходится вводить те или иные параметры, оценить которые возможно либо на основе дополнительных теоретических соображений, либо исходя из экспериментально устанавливаемых свойств. Соотношением (93) в качестве одного из таких свойств привлекается электронная плотность, определяемая экспериментально в процессе рентгеноструктурного исследования.

Схематически это осуществляется следующим образом. Допустим, что волновые функции задаются лишь приближенно и определяются через совокупность параметров α_i, i= 1, 2, ... Соотношение (93) имеет, следовательно, смысл лишь приближенного равенства.

Выполним обращение Фурье обеих частей равенства. В левой части по (33) получим структурную амплитуду 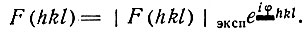. Обращение Фурье правой (теоретической) части имеет вид

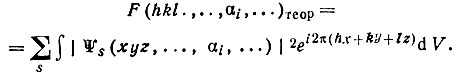(94)

Эта величина - функция не только целочисленных индексов hkl, но и искомых параметров α_i.

Составим функционал:

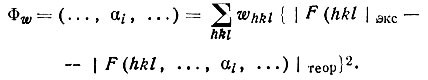(95)

Требуется найти такие α_i, которые делали бы этот функционал минимальным. Вопрос, следовательно, сводится к решению системы уравнений

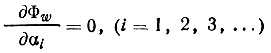(96)

относительно неизвестных α_i.

Если задача заключается лишь в уточнении параметров α_i по структурным данным, то ее решение попадает в рамки метода наименьших квадратов, описанного в предыдущем разделе [с заменой ξ_i на α_i в уравнении (78)].

Более конкретные формулы и схемы использования структурных задач в квантовой химии зависят от метода, принятого при решении уравнения Шредингера системы.