Электронная оболочка атома и спектры

Впервые идеи о сложной структуре атома были высказаны русскими учеными М. А. Павловым, Б. Н. Чичериным и Н. А. Морозовым, но только в 1911 г. английскому физику Э. Резерфорду удалось разработать планетарную, или ядерную, модель строения атома. К ядерной модели атома Резерфорд пришел в результате исследования рассеивания α-лучей, проникающих сквозь тонкую металлическую фольгу (рис. 2). Для большинства α-частиц прямолинейная траектория их полета не менялась. Однако в единичных случаях наблюдалось изменение траектории полета α-частицы, что можно было объяснить только сильным электростатическим отталкиванием положительно заряженной α-частицы от одноименно заряженной части атома, заряд которой и должен быть сосредоточен в меньшем объеме по сравнению с объемом всего атома. Эта часть атома была названа ядром. Чадвик, ученик Резерфорда, по углу отклонения траектории α-частицы (отклонение на некоторый угол φ, φ' или отталкивание почти под углом 180°) вычислил величину положительного заряда ядра атомов ряда элементов, совпавшую с величиной, находимой по методу Мозли из рентгеновских спектров. Было установлено, что радиус ядра в десятки тысяч раз меньше радиуса атома в целом. Именно поэтому Резерфорд образно говорил, что атом в основном - пустота.

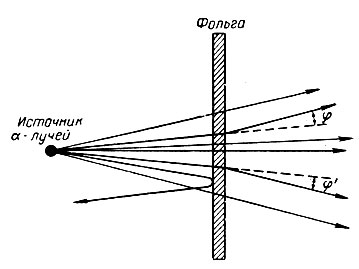
Рис. 2. Рассеивание α-лучей при прохождении через металлическую фольгу

Эрнест Резерфорд (1871-1937)

Так как, по мнению Резерфорда, атом является системой электронейтральной, то естественным оказалось утверждение, что положительное ядро окружено движущимися электронами, число которых равно заряду ядра или порядковому номеру. Совокупность всех электронов, окружающих данное ядро, получила название электронной оболочки атома.

Планетарная модель атома сыграла важную роль в начальной стадии изучения строения атома. Однако ряд вопросов оставался нерешенным. Например: Изменяется ли во времени энергия движущегося вокруг ядра электрона? На каких расстояниях от ядра движется электрон? Как объяснить линейный спектр атомов элементов?

Значительный шаг в развитии теории строения атома был сделан в 1913 г. датским физиком Н. Бором. Используя квантовые представления о природе излучения, введенные немецким физиком М. Планком, он высказал ряд постулатов относительно величины энергии движущегося электрона в атоме водорода. В обычных условиях единственный электрон в атоме водорода вращается вокруг ядра на расстоянии от него, разном 0,53 А^*. Энергия электрона при этом не изменяется; такое состояние атома водорода и называют нормальным или основным. В этом состоянии энергия связи электрона с ядром максимальна - 13,6 эв^**.

^* (Ангстрем (А) - одна стомиллионная доля сантиметра.)

^** (Электрон-вольт (эв) - энергия, которую приобретает электрон при перемещении в электрическом поле в вакууме с разностью потенциалов 1 вольт.)

Нильс Бор (1885-1962)

При сообщении атому водорода энергии извне он поглощает энергию определенными порциями - квантами. Квант энергии E = h·v, где h = 6,62517·10^-27 эрг·сек - постоянная величина, называемая постоянной Планка, a v - частота колебаний (сек^-1). В зависимости от числа поглощенных квантов энергия электрона увеличивается до E₂, E₃, ..., Е_n (где n - любое целое число) и электрон переходит из нормального в различные возбужденные состояния. Причем между состояниями с энергиями Е₂ и Е₃ или Е₃ и E₄ не может быть ни одного промежуточного. Отвечающие этим энергиям уровни были названы энергетическими или квантовыми уровнями (рис. 3). Про электрон, находящийся в данном энергетическом состоянии, стали говорить, что он находится на данном уровне. Расстояние электрона от ядра в атоме определяется энергетическим состоянием электрона, т. е. каждому электрону соответствует свой энергетический уровень. Расстояние электрона от ядра в атоме водорода можно вычислить по формуле Н. Бора r_n = 0,53·n² А (где r_n, так называемые, боровские радиусы); радиусы относятся между собой как квадраты целых простых чисел, т. е. как 1²:2²:3²: ...: n². Чем дальше электрон отстоит от ядра, тем он слабее связан с последним; энергия связи определяется по формуле Е_св = - 13,6/n² эв (знак минус указывает, что возбуждение электрона требует затраты энергии).

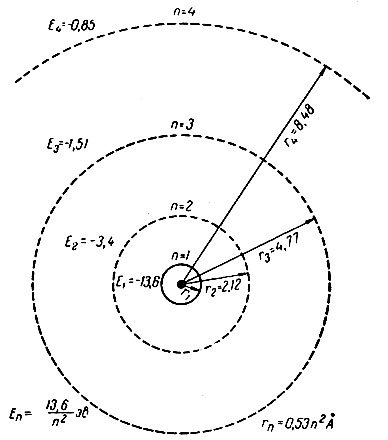
Рис. 3. Энергия электрона атома водорода в нормальном и возбужденном состояниях (по Бору)

Следовательно, энергия электрона в атоме, а значит и расстояние от ядра атома, на котором может находиться электрон, определяются значением особого числа n, названного главным квантовым числом, имеющим значение 1, 2, 3, 4, ..., n.

В возбужденном состоянии электрон обычно пребывает лишь 10^-8 сек и по истечении этого короткого времени возвращается в менее возбужденное или нормальное состояние. В этом случае говорят, что электрон переходит с высокого энергетического уровня на более низкий (или просто - с высокого уровня на низкий уровень). Конечно, никаких уровней в атоме нет; говоря так, понимают лишь энергетическое состояние электрона, что и определяет его положение в атоме. При переходе электрона с уровня на уровень разность энергий выделяется в виде излучения, характеризующегося определенной частотой v или длиной волны λ.

Каждому отдельному переходу электрона с уровня на уровень соответствует определенная линия в оптическом спектре. Совокупность линий, отвечающая переходу электронов с любых квантовых уровней на какой-либо один, называется спектральной серией. Так, при переходе с любого энергетического уровня на первый возникает серия линий, лежащих в коротковолновой части спектра - серия Лаймана. Серия линий, лежащих в видимой части спектра - серия Бальмера, возникает при переходе электронов с более дальних энергетических уровней на второй. При переходе электронов с дальних энергетических уровней на третий, четвертый и пятый получаются длинноволновые серии, отвечающие инфракрасной части спектра. Совокупность всех серий называется оптическим спектром (рис. 4). В настоящее время для водорода известны шесть спектральных серий, получивших свои названия по имени ученых, обнаруживших эти серии экспериментальными методами.

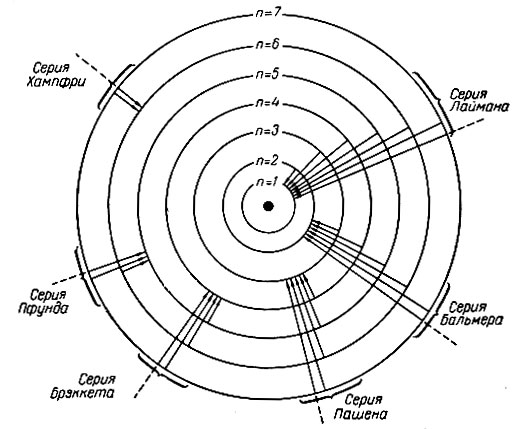
Рис. 4. Схема возникновения спектральных серий оптического спектра водорода

Зная полную энергию электрона (она равна сумме кинетической и потенциальной энергий) на дальнем E_д и ближнем E_б квантовых уровнях, можно вычислить частоту излучения по формуле Бора v = (Е_д - E_б)/h. Длина волны, отвечающая данной частоте, может быть рассчитана по формуле λ = c/v, где с - скорость света. Сопоставим значения длин волн, вычисленных по формуле Н. Бора и найденных экспериментально (табл. 19). Совпадение данных настолько близко, "...что истинная природа атомной структуры угадана глубоко и верно", как отмечал в одной из своих работ академик С. И. Вавилов.

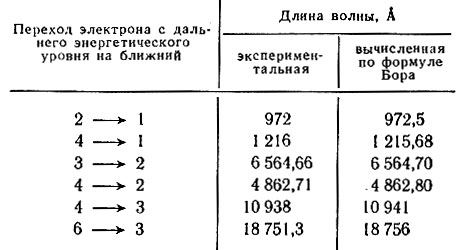
Таблица 19. Длины некоторых волн в оптическом спектре водорода

Теория строения атома Бора позволила не только качественно, но и количественно расшифровать механизм возникновения оптического спектра самого простого атома - атома водорода. Однако попытки использовать теорию Бора для объяснения ряда особенностей в строении более сложных атомов не привели к положительным результатам.

Впоследствии оказалось, что для характеристики электрона в атоме недостаточно знать только одно главное квантовое число n. Изучение тонкой структуры спектральных линий, расщепление их на составные компоненты под влиянием электрического и магнитного полей и наличие собственного момента движения электрона или спина (вращение вокруг собственной оси) показали, что для оценки состояния электрона в атоме необходимо пользоваться четырьмя квантовыми числами: n, l, m и s.

Для нормальных состояний атомов всех известных элементов n может иметь значение от 1 до 7, т. е. электроны электронной оболочки самых сложных атомов располагаются на семи уровнях (слоях). Максимальное число электронов на n-уровне можно найти по формуле Х_n = 2n². Например, на первых четырех уровнях максимально может разместиться:

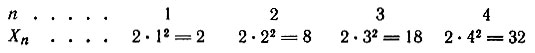
Из восьми электронов второго уровня два электрона несколько отличаются по своей энергии от остальных шести. Таким образом было установлено, что энергетические уровни расщепляются на подуровни и электроны одного уровня располагаются на разных подуровнях, число которых равно номеру уровня, т. е. первый уровень включает один подуровень, второй - два, третий - три, четвертый - четыре и т. д. Каждому подуровню отвечает определенное значение орбитального квантового числа l = 0, 1, 2, 3, ..., (n - 1). Физический смысл этого квантового числа заключается в том, что движущийся вокруг ядра электрон создает орбитальный механический момент, возможные значения которого и определяются величинами l. Обычно вместо числовых значений l применяют буквенные обозначения, а именно: для l = 0 букву s, для l = 1 - р, для l = 2 - d и для l = 3 - f. Максимальное число электронов в подуровне (X_l) определяется по формуле X_l = 2(2l + 1). Например, 32 электрона в четвертом уровне (n = 4) распределятся по четырем подуровням следующим образом:

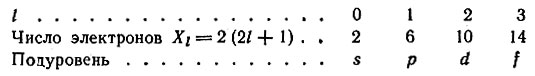
Максимальная емкость подуровней записывается так: s²p⁶d¹⁰f¹⁴. Числа в правом верхнем углу символа, обозначающего подуровень, равны максимально возможному числу электронов данного подуровня.

Зная порядковый номер элемента, т. е. заряд ядра его атома, а следовательно, и число электронов в атоме, можно проследить распределение этих электронов по энергетическим уровням и подуровням. Суммарная запись распределения максимального числа электронов в атоме по уровням 1, 2, 3 и 4 и возможным подуровням имеет вид:

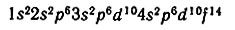
Например, 12 электронов в оболочке атома магния (Z = 12) следующим образом распределятся по уровням и подуровням:

Условно распределение электронов в атоме магния можно записать: 1s²2s²2p⁶3s².

Из схемы и записи распределения видно, что в атоме магния три энергетических уровня и на внешнем из них содержится два s-электрона.

Шесть электронов р-подуровня характеризуются также различным энергетическим состоянием. Подуровни в атоме подразделяются на энергетические группы, или атомные орбитали. Число атомных орбиталей в подуровне равно максимальному числу электронов в нем, деленному на два. Так, на s-подуровне - одна атомная орбиталь (2 : 2=1), р-подуровне - три (6:2 = 3), d-подуровне - пять (10 : 2 = 5) и на f-подуровне семь атомных орбиталей (14:2 = 7). Каждой атомной орбитали отвечает определенное значение магнитного квантового числа т. Это квантовое число позволяет определить проекции орбитального механического момента на произвольно выбранное направление. Магнитное квантовое число может принимать значения от +l до -l, включая нулевое, где l - орбитальное квантовое число. Так, при l = 1 (р-подуровень) m может иметь только три значения: +1, 0, -1, которые отвечают трем орбиталям.

На любой атомной орбитали максимально может находиться два электрона, отличающиеся друг от друга тем, что вращаются вокруг своей оси в противоположном направлении. Следовательно, их собственные моменты количества движения, называемые спинами, также противоположны. Спин характеризуют спиновым, квантовым числом, которое определяет величину проекции спина. Спиновое квантовое число s может иметь два значения: +¹/₂ и -¹/₂.

Таким образом, каждый электрон атома характеризуется четырьмя квантовыми числами: n - определяющим энергетический уровень, l - соответствующим подуровню, m - отвечающим орбитали и s - говорящим о спине электрона. Электроны располагаются в атоме в "разрешенном" порядке, определяемом принципом, или "запретом", Паули:

"В атоме не может быть двух электронов, обладающих одинаковыми значениями всех четырех квантовых чисел".

Следовательно, каждые два электрона, даже если у них одинаковые n, l и m, должны различаться значениями s. Например, со значениями n = 1, l = 0 и m = 0 может быть только два электрона, располагающиеся на одной орбитали и, следовательно, различающиеся спиновым квантовым числом s:

При графическом изображении распределения электронов по орбиталям орбиталь изображают в виде прямоугольника, а электроны с разными спинами, находящиеся на орбитали, - в виде стрелок, направленных в противоположные стороны:  

В атомной орбитали могут находиться:

либо одиночные (или непарные) электроны  

либо парные электроны с антипараллельными спинами  

В последнем случае суммарный спин электронов равен нулю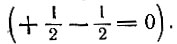  

Атомные орбитали, подуровни и уровни с суммарным значением спина, равным нулю, называются замкнутыми. Суммарный электронный спин атома в целом определяется лишь наличием одиночных, или непарных, электронов.

Определить однозначно, как распределяются электроны в атоме, зная все четыре квантовые числа - n, l, m и s - и исходя из принципа Паули, не всегда возможно. Распределение в данном подуровне числа электронов, равного или меньшего половины максимальной емкости подуровня (т. е. для р ≤ 3, d ≤ 5 или f ≤ 7 электронов), теоретически может быть самым разнообразным. Допустим, например, что по атомным орбиталям распределяется в р-подуровне три электрона, в d-подуровне - четыре и в f-подуровне - шесть электронов. В этом случае можно составить, по крайней мере, по две комбинации распределения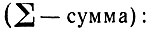  

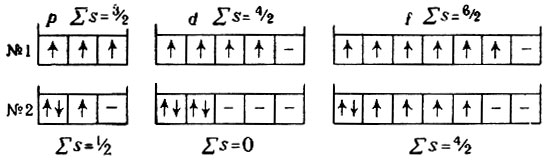
Как видно, в комбинации распределения № 1 занято большее число атомных орбиталей и суммарный спин электронов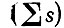  
больше, чем в комбинациях № 2. Возможная комбинация распределения электронов определяется правилом Гунда:

"В данном подуровне электроны должны занять по возможности все свободные орбитали, так как при этом суммарный спин электронов достигает наибольшего значения".

Этому правилу отвечает только комбинация № 1. В качестве примера рассмотрим строение атомов кислорода и натрия. На основании всего сказанного возможны только такие схемы распределения электронов в оболочке:

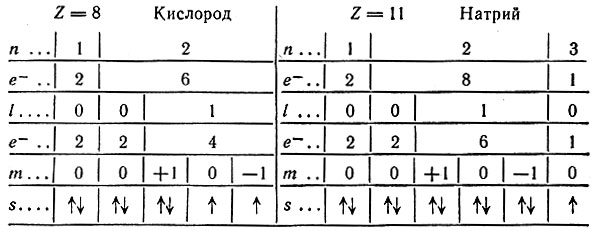
Из схем следует, что в атоме кислорода из шести внешних электронов одиночными являются два, а в атоме натрия - один внешний электрон. Электронная оболочка атома кислорода состоит из двух уровней, а атома натрия - из трех.

Таким образом, атомы имеют как бы слоистую структуру, и аналогичные внутренние уровни у атомов всех элементов построены одинаково. Однако чем больше Z, тем сложнее становится закономерность, определяющая последовательность заполнения электронами энергетических подуровней в атоме. Общим является только то, что электрон стремится занять подуровень энергетически более выгодный (наиболее низкий). Именно поэтому 19-й электрон атома калия располагается не на 3d-подуровне, а на 4s. Точно также подуровень 5s заполняется раньше, чем 4d, а подуровень 5р раньше подуровня 4f. Условно энергетические подуровни в атоме можно представить по их величине и порядку заполнения следующим образом:

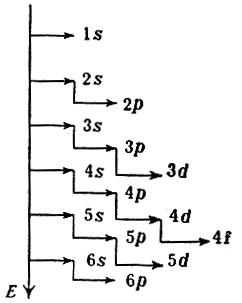
Наиболее существенную роль в раскрытии тайн строения атома сыграл метод спектрального анализа. Следует различать оптические и рентгеновские спектры.

Оптический спектр является отображением всех возможных "незапрещенных" переходов электрона из возбужденных состояний в менее возбужденные или в основное состояния (внешний уровень). Оптические спектры очень сложны. Они состоят из десятков, сотен и тысяч спектральных линий.

Рентгеновский спектр возникает при переходе электронов на вакантное место внутренних электронных уровней, образовавшееся в результате возбуждения атома вследствие соударения с электроном или фотоном (электронный или фотонный удар) при рентгеновском облучении. Если электроны перемещаются на самый близкий к ядру внутренний слой, то возникает серия К рентгеновского спектра; при переходах на иные внутренние слои появляются другие серии (рис. 5). Для самых сложных атомов известны семь серий рентгеновского спектра K, L, M, N, О, Р, и Q, отвечающих семи энергетическим уровням в электронной оболочке атома.

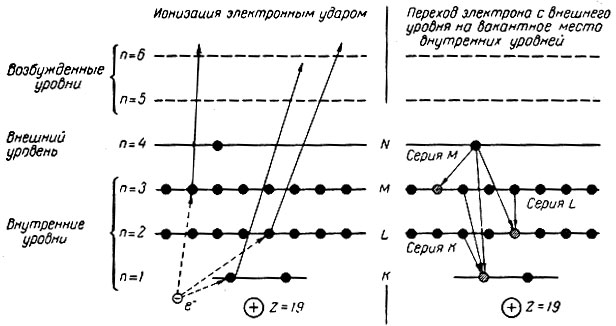
Рис. 5. Схема возникновения рентгеновского спектра калия (Z = 19; 1s²2s²2p⁶3s²3p⁶3d⁰4s¹

От оптических спектров рентгеновские спектры отличаются небольшим числом линий, например, в серии К всего пять линий.

Выше отмечалось, что по длинам волн характеристического рентгеновского излучения можно определить важнейшую количественную характеристику элементов - порядковый номер.

Расшифровка оптических спектров элементов, атомы которых имеют сложное строение, представляет собой трудную задачу. Здесь в упрощенной форме рассматриваются некоторые общие вопросы расшифровки оптических спектров водородоподобных атомов. Водородоподобными атомами называются атомы, состоящие, подобно атому водорода, из ядра и одного электрона. Такими атомами являются ионизированные атомы с Z ≥ 2, потерявшие все электроны, кроме одного. Например, если от атома лития, имеющего три электрона (Z = 3), оторвать два электрона, то получим водородоподобный изонизированный атом лития Li²⁺. Энергия (в эв) электрона в квантовом уровне сложного атома определяется по формуле Е = - 13,6(Z^*)²/n². Здесь Z^* - эффективный заряд ядра, равный Z - σ, где σ - коэффициент экранирования, характеризующий уменьшение силы притяжения внешнего электрона к ядру вследствие отталкивания его остальными электронами; для водородоподобных атомов σ = 0.

В спектроскопии энергию электрона принято выражать определенным термом (T), который находят делением энергии (E), выраженной в эргах, на скорость света (с) и постоянную Планка (h), т. е. Т = E/ch.

Одиночному электрону отвечает определенное значение орбитального квантового числа l. Если в атоме несколько электронов, то отдельные орбитальные моменты складываются в суммарный орбитальный момент L. Каждому значению L отвечает свой терм. Суммарные орбитальные моменты L обозначаются теми же буквами, что и орбитальный момент электрона, но только не строчными (s, р, d ...), а прописными (S, Р, D ...), теми же буквами обозначаются и соответствующие термы. Таким образом, возможные числовые значения суммарных орбитальных моментов и принятые обозначения их и их термов следующие:

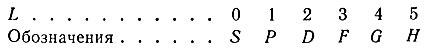
Аналогично рентгеновскому спектру важнейшие линии в оптическом спектре группируются в серии: главную, резкую, диффузную и фундаментальную (основную). Спектральные линии названных серий образуются при следующих переходах электронов:

Термы, отвечающие этим переходам электронов, многообразны. Терм, соответствующий наименьшей энергии, называется основным. Например, из схемы возникновения оптического спектра натрия (рис. 6) следует, что основной терм - ²S, а все другие термы являются возбужденными. В данной схеме указаны только наиболее важные спектральные линии, а в действительности их значительно больше. Так, в главной серии оптического спектра натрия можно наблюдать не менее 57 спектральных линий.

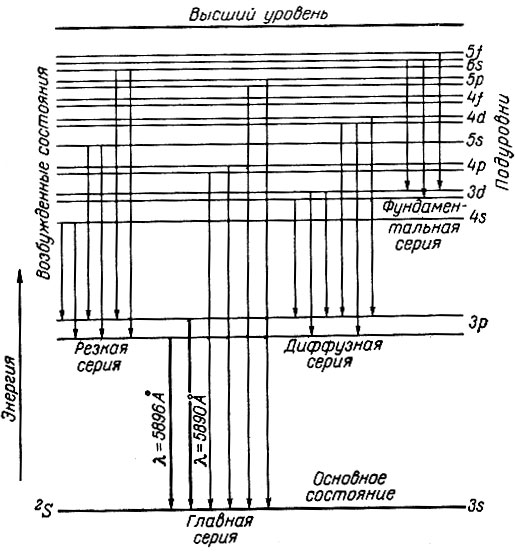
Рис. 6. Схема возникновения оптического спектра натрия

С помощью спектроскопов большой разрешающей силы было обнаружено, что многие спектральные линии состоят из двух, трех или большего числа тонких линий. Например, в главной серии оптического спектра натрия наблюдаются двойные (дублетные) линии с длинами волн 5890 и 5896 А. Этот эффект вызван тем, что все термы, кроме S-термов (последние на схеме обозначены каждый одной горизонтальной линией, отвечающей состоянию 3s, 4s, 5s или 6s), расщепляются на ряд близких энергетических состояний (на схеме они обозначены двойными линиями), или, как говорят, обладают мультиплетностью (М)^*. Мультиплетность может быть меньше и больше двух, т. е. термы могут быть синглетные (одиночные), дублетные, триплетные, квартетные и более сложные. Мультиплетность терма обозначается числовым индексом при буквенном обозначении терма. Например, ²S означает "дублетный терм S". Основное состояние натрия характеризуется этим термом (см. схему).

^* (Объем этой книги не позволяет детально анализировать явление мультиплетности. Здесь рассматриваются лишь некоторые общие положения.)

Мультиплетность спектра позволяет определить число непарных электронов в атоме, которое на единицу меньше мультиплетности. Так, в атоме натрия должен быть один непарный электрон, ибо разность М - 1 = 2 - 1 = 1. Действительно, у натрия Z = 11 и формула распределения электронов будет: 1s²2s²2p⁶3s¹, т. е. непарным является один электрон, расположенный на 3s-подуровне. Для кислорода характерен терм 3Я, что свидетельствует о наличии в его атоме двух непарных электронов (Z = 8; 1s²2s²2p⁴; см. схему распределения электронов на стр. 66). При терме ¹S число непарных электронов равно нулю. Таким термом обладают атомы благородных газов, бериллия и щелочноземельных металлов, цинка, кадмия, ртути и палладия. Терм ⁷S характерен для атома, имеющего шесть непарных электронов, из которых один s- и пять d-электронов (атом хрома). По спектроскопическим данным определяются термы элементов и расшифровывается строение электронных оболочек их атомов.

Мультиплетность терма (М) - чисто физическое свойства атома - оказалось связанным с основным химическим свойством элементов - валентностью (В), в ее классическом представлении. По Льюису - Лондону, валентность определяется числом непарных электронов в атоме, т. е. валентность на единицу меньше мультиплетности (В = М - 1). Следовательно, оптические спектры тесно связаны с конструкцией периодической системы, в которой номера групп указывают на характеристичную валентность элементов.

Периодичность в изменении свойств элементов получила объяснение не только на основе закономерного изменения структуры электронной оболочки атомов, но и на основе периодического изменения мультиплетности термов. При движении по периоду слева направо в системе элементов мультиплетность возрастает с попеременным чередованием четности (дублет, квартет, секстет, октет) и нечетности (синглет, триплет, квинтет, септет). В спектрах испускания, полученных в пламени электрической дуги (дуговые спектры), для элементов, атомы которых имеют нечетное число электронов, наблюдается четная мультиплетность, и наоборот (табл. 20).

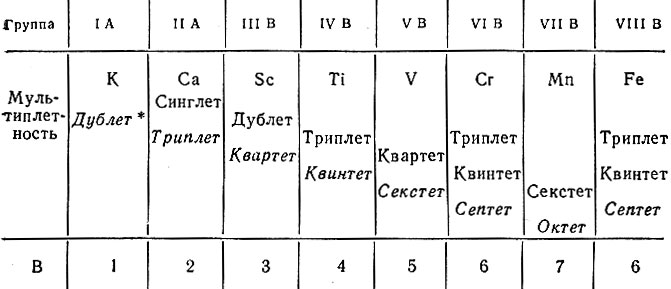
Таблица 20. Изменение мультиплетности и характеристичной валентности у элементов начала четвертого периода

^* (Курсивом набраны термы, которые отвечают характеристичной валентности (В) элементов.)

Для основного состояния атомов элементов 2-го периода в зависимости от числа эквивалентных s- и p-электронов (эквивалентными называются электроны с одинаковыми значениями квантовых чисел n и l) термы обозначаются так:

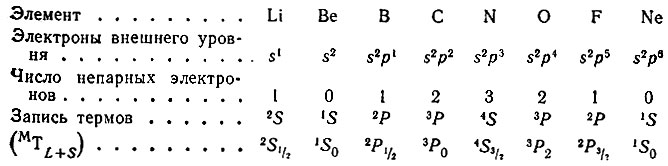
Индексами внизу справа отмечаются квантовые числа J, определяющие полный момент атома в целом J = L + S (L - суммарный орбитальный момент, S - суммарный спиновый момент).

s- и р-элементы одной и той же группы периодической системы характеризуются одинаковым основным термом. Так, термы всех щелочных металлов - ²S, а отсюда В = 1, и, действительно, характеристическая валентность этих элементов равна 1.

Основной терм атомов d-элементов зависит от суммарного числа эквивалентных s- и d-электронов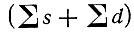  
и от числа s-электронов (n) во внешнем уровне (sⁿ):

Вследствие наблюдающегося "провала" электронов у атомов d-элементов, являющихся аналогами, термы основного состояния могут быть различными. Например, у элементов-аналогов VIB-группы - хрома, молибдена и вольфрама, электронные конфигурации отличаются и термы в основном состоянии будут неодинаковые:

Как отмечалось выше, терм основного состояния бериллия и щелочноземельных металлов (Mg, Ca, Sr, Ba, Ra) должен быть ¹S, а следовательно, мультиплетность М = 1 и характеристическая валентность В = М - 1 = 0. Но, как известно, эти элементы в соединениях проявляют валентность, равную 2. Как же эта объяснить? Дело в том, что, помимо основного состояния, за счет подвода энергии извне, атомы могут быть переведены в возбужденное состояние при условии, что в подуровнях атомов имеются незанятые места (орбитали). Например, во внешнем уровне атома кальция (n = 4) два парных электрона занимают s-подуровень (конфигурация атома - 4s²). Но на этом же уровне имеется p-подуровень с тремя незанятыми орбиталями, на одну из которых может быть переведен один из электронов 5-подуровня. Атом кальция в возбужденном состоянии (конфигурация - 4sp) имеет два непарных электрона, характеризуется мультиплетностью М = 3 и валентностью В = М - 1 = 2. Действительно, в спектре кальция и других щелочноземельных металлов (см. табл. 20) обнаруживается как синглет (М = 1), так и триплет (М = 3).

Если разность между энергиями подуровней невелика, то возможность возбуждения реально осуществима, что и имеет место. Увеличение числа непарных электронов приводит к возрастанию валентности. Например, алюминий может проявлять валентность - 1 и 3, кремний - 2 и 4, фосфор - 3 и 5, сера - 2, 4 и 6 и т. д. Возбуждению атомов сопутствует явление гибридизации, о чем будет сказано ниже (см. стр. 103, 124-126).

Причина многообразия валентности элементов объясняется различной мультиплетностью термов одного и того же элемента. Так как термы высокой мультиплетности (септеты, октеты, нонеты) проявляются редко, то и высшая валентность наблюдается относительно редко.