Глава 1. Основы теории атома

Поведение макроскопических тел описывается законами Ньютона классической механики, а поведение атомов - законами квантовой механики. И те и другие законы основаны на эксперименте. Мы не можем вывести уравнение классической механики, согласно которому сила равна произведению массы на ускорение. Однако это уравнение удовлетворяет нас, поскольку оно дает правильные результаты в задачах классической механики. Аналогичным образом будем рассматривать и уравнения квантовой механики: окончательный критерий их справедливости - согласие с экспериментом полученных при их решении результатов.

Свойства интерференции и дифракции видимого света указывают на то, что он имеет волновой характер. Максвелл показал, что видимый свет составляет лишь часть электромагнитного излучения, которое распространяется в пространстве с постоянной скоростью с (2,998·10¹⁰ см/сек в вакууме) и представляет собой гармонически осциллирующие электрическое и магнитное поля. Это излучение характеризуется частотой (ν) или длиной волны (λ), которые связаны соотношением с = νλ. Спектр электромагнитного излучения условно разбивают на несколько областей в соответствии с длиной волны λ (см. рис. 1.1).

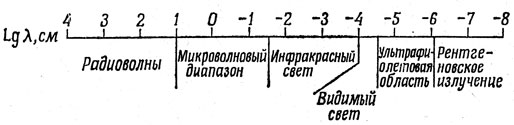
Рис. 1.1. Электромагнитный спектр

Излучение или поглощение электромагнитных волн телом происходит таким образом, что в конце концов устанавливается равновесие с окружающей средой. Интенсивность равновесного излучения (так называемого излучения абсолютно черного тела) зависит от температуры. На рис. 1.2 представлено распределение энергии в спектре абсолютно черного тела для различных температур. Планк показал, что это распределение можно объяснить, если предполагать, что тело содержит осцилляторы всевозможных частот, которые могут поглощать или испускать электромагнитные волны. Однако согласие с экспериментом можно получить только в том случае, если предположить, кроме того, что осциллятор, испускающий излучение частоты ν, может поглощать энергию только дискретными порциями величины hν (h называется постоянной Планка и равна 6,6·10^-27 эрг·сек; hν - энергия кванта). Это было первое предположение о том, что атомные системы (осцилляторы) пребывают только в дискретных энергетических состояниях.

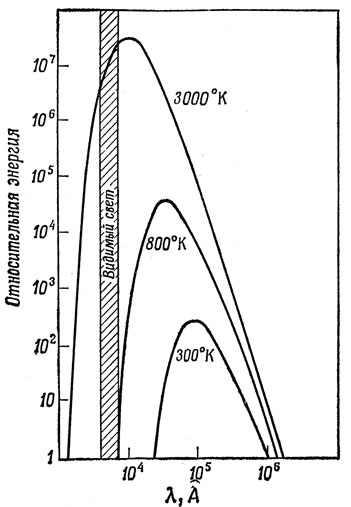
Рис. 1.2. Зависимость распределения энергии в спектре излучения черного тела от температуры

Когда свет падает на металл, из металла могут быть вырваны электроны. Это не удивительно, поскольку свет представляет собой электромагнитное излучение. Но особенности этого фотоэлектрического эффекта нельзя понять, исходя только из волновой природы света. Оказывается, что электроны совершенно не испускаются, если частота света не превышает некоторого минимального значения; если же частота света достаточно высока, то число испускаемых электронов пропорционально интенсивности света; однако энергия их зависит только от частоты падающего света. Эйнштейн показал, что эти факты можно понять, если предположить, что свет ведет себя как пучок частиц, каждая с энергией hν. Он предсказал, что кинетическая энергия выбитых электронов должна определяться соотношением

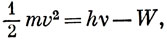
где W - минимальная энергия, необходимая для выбивания электрона из металла (ее называют работой выхода). Позднее эти выводы были экспериментально подтверждены.

Результаты, полученные Планком при изучении равновесного излучения и Эйнштейном при исследовании фотоэффекта, можно объединить, связав энергию и частоту соотношением

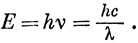
Оно известно как соотношение Планка - Эйнштейна и применимо к атомным осцилляторам и к свету.

В 1911 г. Резерфорд предложил модель атома, основные идеи которой остались неизменными. Диаметр атома равен приблизительно 10^-8 см (единица длины 10^-8 см называется ангстремом и обозначается А), однако эксперименты по рассеянию α-частиц (ионов Не²⁺) показали, что рассеивающим центром в атоме является малое положительно заряженное ядро (с диаметром 10^-13-10^-12 см). Оно окружено электронами, которые занимают остальной объем атома. Масса электрона составляет 1/1840 часть массы протона.

Детали структуры ядра - область, которую изучают физики. При химическом подходе достаточно сказать, что ядро состоит из протонов и нейтронов, имеющих одинаковые массы. Заряд протона равен заряду электрона по величине и противоположен ему по знаку. Нейтрон - нейтральная частица. Он был открыт Чэдвиком в 1932 г., хотя Резерфорд предсказал существование нейтрона еще раньше. В нейтральном атоме число электронов равно числу протонов, и это число есть атомный номер.

Общее число протонов и нейтронов в ядре называют массовым числом, а атомы с данным атомным номером и различными массовыми числами - изотопами. Например, известны пять изотопов свинца с массовыми числами 206, 207, 208, 210 и 214. Все они содержат 82 протона, но разное число нейтронов в соответствии со значением массового числа. Атомный вес обычного свинца равен 207,2^*), изотопы ²⁰⁶Pb и ²⁰⁸Pb являются наиболее распространенными и встречаются почти одинаково часто.

^*) (В настоящее время за единицу измерения атомных весов принята ¹/₁₂ веса наиболее часто встречающегося изотопа углерода (с массовым числом 12).)

Согласно классической механике, атом Резерфорда не может быть устойчивой статической системой. Если бы это было так, то электроны упали бы на ядро. Но даже динамическая модель, в которой электроны движутся вокруг положительного ядра, с классической точки зрения нестабильна, поскольку электроны будут взаимодействовать с электрическим полем ядра, излучать энергию и, двигаясь по спирали, падать на ядро. Однако при отсутствии внешнего воздействия атомы не излучают, а при его наличии атомы излучают лишь дискретный набор частот, характерный для данного атома.

Атомы водорода могут излучать в видимой области спектра свет четырех длин волн: λ = 6563 4861, 4341, 4102 А. В 1895 году Бальмер установил, что эти четыре числа укладываются в формулу

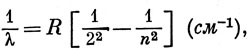
где n = 3, 4, 5 и 6, a R - постоянная Ридберга, равная 109678 см^-1. Позднее в инфракрасной и ультрафиолетовой областях спектра были обнаружены другие линии, и Ритц показал, что их длины волн подчиняются аналогичной формуле

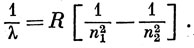
В спектре излучения водорода найдены 5 серий линий, которые названы по имени обнаруживших их ученых:

Другие атомы не имеют столь простой спектральной картины. Но во всех случаях спектральные линии можно описывать формулами, аналогичными формуле (1.4), хотя n₁ и n₂ - не обязательно равны целым числам.

В 1913 г. Бор предложил теорию строения атома, которая объясняет эти результаты спектральных наблюдений. В теории Бора электроны, движущиеся по орбитам вокруг ядра, рассматриваются на основе классической механики. Однако для объяснения того обстоятельства, что электроны не падают по спирали на ядро, Бор ввел квантовые условия, определяющие допустимые орбиты движения электронов. Далее, Бор постулировал, что переходы электронов с одной орбиты на другую возможны только в том случае, если различие в энергиях электрона компенсируется поглощением или излучением, причем частоту поглощенного или излученного кванта связана с разностью энергий соотношением Планка - Эйнштейна.

Налагая ограничения на допустимые орбиты и энергии разрешенных переходов электрона, Бор объяснил с помощью созданной им теории спектр атома водорода. Целые числа, содержащиеся в формуле Ритца, связаны с так называемыми квантовыми числами в теории Бора. Истинным триумфом теории Бора было, однако, не объяснение спектральной картины, а выражение постоянной Ридберга через фундаментальные константы^*):

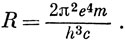
^*) (Стандартные обозначения, использованные в этой книге, приведены в списке, помещенном в начале книги.)

Вычисленное значение постоянной Ридберга согласуется с экспериментальным с точностью до 0,02%.

В течение десяти лет теория Бора применялась для объяснения спектральных явлений, главным образом Бором, а также Зоммерфельдом. Однако эта теория эклектична, поскольку в ней квантовые условия не появляются естественно, а вводятся для того, чтобы получить соответствие с экспериментом. Еще более серьезным недостатком этой теории является ее неспособность объяснить тонкую структуру спектральных линий атомов, отличных от атома водорода.

Пользуясь уравнениями Максвелла, можно показать, что если электромагнитное излучение содержит волновые пакеты с энергией hν, то эти пакеты обладают импульсом hν/c. В 1923 г. Комптон подтвердил это экспериментально, изучая рассеяние рентгеновских лучей электронами в графите, в результате которого возникают свободные электроны. Анализируя изменение частоты рентгеновских лучей в зависимости от угла рассеяния, он показал, что столкновение фотона и электрона подчиняется законам сохранения энергии и импульса классической механики и что импульс рентгеновских лучей действительно равен hν/c или h/λ. Это было новым подтверждением корпускулярной природы света.

Таким образом, до сих пор мы не встречались ни с чем таким, что было бы совершенно неприемлемо с точки зрения классической физики. Загадочной является все же двойственная корпускулярно-волновая природа света. В явлениях дифракции и интерференции свет ведет себя подобно волне, а в фотоэлектрическом эффекте и эффекте Комптона - как поток частиц.

В 1923 г. де Бройль связал идеи теории относительности с идеями Планка и Эйнштейна. В теории относительности энергия связана с массой, а в соотношении Е = hν - с частотой. Объединяя эти соотношения, можно получить связь массы с частотой. Другими словами, вещество подобно свету имеет волновую природу. Де Бройль предположил, что частица с импульсом p обладает связанной с ним длиной волны

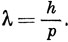
Это есть то же самое соотношение, которое имеет место для импульса фотонов^*).

^*) (В классической нерелятивистской механике масса и импульс связаны соотношением

p = mυ.

В релятивистской механике оно заменяется следующим соотношением:

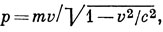
где m - масса покоя. Поэтому частица, обладающая отличной от нуля массой покоя и движущаяся со скоростью света, имеет бесконечный импульс. Фотон, однако, характеризуется нулевой массой покоя и конечным импульсом, определяемым соотношением (1.6).)

Например, электрон, ускоренный под действием разности потенциалов 100 в, имеет кинетическую энергию 100 эв (1 эв = 1,6·10^-12 эрг). Для этого электрона (масса 9,1·10^-28 г) р²/2m = 1,6·10^-10; р = 5,4·10^-19 г·см/сек; λ = 1,2·10^-8 см.

Для того чтобы получить дифракцию волн, необходима регулярная система центров дифракции с расстоянием между ними порядка λ. Решетками с постоянными порядка 10^-8 см обладают ионные кристаллы и металлы. Соотношение де Бройля было подтверждено Дэвиссоном и Джермером (1927 г.) и Томпсоном (1928 г.) путем наблюдения дифракционной картины (аналогичной рассеянию рентгеновских лучей), возникающей при бомбардировке металла пучком электронов.

Таким образом, эксперимент показал, что и вещество и излучение имеют двойственные корпускулярно-волновые свойства. Они ведут себя как волны в одних условиях и как пучок частиц в других; это зависит от характера эксперимента. Следует подчеркнуть, однако, что мы не рассматриваем вещество и излучение как два различных аспекта одной и той же субстанции. Например, электрон обладает зарядом и массой, а фотон не имеет ни массы, ни заряда. Дифракционная картина, возникающая при облучении кристалла рентгеновскими лучами, в общем, похожа на ту, которая возникает при падении пучка электронов на кристалл, но они не идентичны. Распределения интенсивности в обеих картинах различны, так как фотоны взаимодействуют с веществом по другим законам, нежели электроны.

Если электрон обладает волновыми свойствами, то его поведение должно описываться волновым уравнением, подобно тому как описывают световые и звуковые волны, колебания струны и т. п. Такое уравнение было предложено Шредингером в 1926 г. Его можно либо сразу рассматривать как основное уравнение квантовой механики, причем его решения должны приводить к согласию с экспериментом, либо это уравнение может быть выведено из совокупности основных постулатов и экспериментальных данных. На данной стадии изложения мы будем следовать второму подходу, поскольку опыт показывает, что такой подход позволяет легче воспринять волновое уравнение тем, кто впервые приступает к изучению квантовой механики. Однако важно понимать, что это основное уравнение квантовой механики невозможно получить из каких-либо уравнений классической механики, не вводя неклассических постулатов, и что уравнение Шредингера обосновывается тем, что его решения согласуются с экспериментом.

Уравнения классического волнового движения имеют некоторые частные решения, известные как стоячие волны, которые обладают неизмененными во времени точками нулевой амплитуды (узловыми точками). Эти стоячие волны для натянутой струны представляют собой основные колебания струны и обертоны. Их можно нумеровать числами 0, 1, 2 ... по числу узлов в струне между двумя ее концами. Шредингер пришел к заключению, что целые числа, содержащиеся в формуле Ритца и являющиеся квантовыми числами в теории Бора, могут возникнуть аналогичным образом, т. е. из решений электронного волнового уравнения, имеющих вид стоячих волн.

Общее выражение для амплитуды гармонической стоячей волны в одном измерении (х) имеет вид

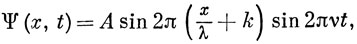
где k - постоянная. Дифференцируя уравнение (1.7) дважды, получим, что Ψ удовлетворяет дифференциальному уравнению

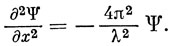
Если теперь введем импульс, пользуясь соотношением де Бройля (1.6), это уравнение примет вид

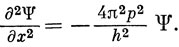
Полная энергия есть сумма потенциальной и кинетической энергий, следовательно,

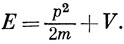
Подставляя р² из уравнения (1.10) в уравнение (1.9), получим

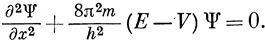
Это одномерное уравнение Шредингера для электрона. Трехмерное уравнение можно записать в виде

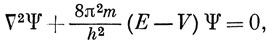
где ∇² - сокращенное обозначение выражения

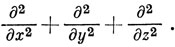
Более общий вывод уравнения Шредингера рассматривается в гл. 6. Ψ представляет собой амплитуду электронной волны и называется волновой функцией. В 1926 г. Борн предположил, что функция Ψ должна быть связана с некоторым физически наблюдаемым свойством электрона через функцию Ψ² (в более общем случае через Ψ^*Ψ¹), если Ψ - комплексная функция), которая интерпретируется как плотность вероятности нахождения электрона в некоторой точке пространства. Эта интерпретация более удовлетворительна, чем та, которую дал сам Шредингер: электрон есть облако заряда, распределенного с плотностью Ψ^2**). Борновская трактовка лучше, поскольку, как видно из дальнейшего, уравнения квантовой механики основаны на представлении об электроне, как о точечном заряде, а не зарядовом облаке. Однако, измеряя среднюю по времени электронную плотность в атоме или молекуле, невозможно различить эти две интерпретации Ψ²; поэтому часто бывает удобно и физически наглядно представлять себе Ψ² как плотность электронного облака.

^*) (Если Ψ - функция, содержащая чисто мнимое число i = √-1, то Ψ^*, комплексно сопряженная с W, получается заменой i на -i в Ψ. Например, если Ψ = а + ib, то Ψ^* = а - ib; если Ψ = ei^x, то Ψ^* = e^-ix. Таким образом, Ψ^*Ψ - вещественная, повсюду неотрицательная функция, которая физически интерпретируется как плотность вероятности нахождения электрона в точке пространства.)

^**) (Данное Шредингером толкование волновой функции не "менее удовлетворительно", а просто ошибочно и может представлять лишь исторический интерес. - Прим. ред.)

Для того чтобы функция Ψ была приемлема с точки зрения физики, необходимо наложить на нее некоторые условия. Так, например, она должна быть однозначной функцией (в любой точке пространства х, у, z иметь единственное значение). Кроме того, поскольку вероятность нахождения электрона хотя бы в какой-нибудь точке пространства равна единице, при интегрировании Ψ² по всему пространству должна получаться единица. Это дает второе условие, которое налагают на функцию Ψ, - так называемое условие нормировки^*):

^*) (По этому вопросу см. также примечание на стр. 93. - Прим. ред.)

Статистическая интерпретация Ψ² как плотности вероятности находится в согласии с волновой природой электрона и принципом неопределенности Гейзенберга (1927 г.). Согласно этому принципу, координата и импульс атомной частицы не могут быть одновременно измерены точно; измеряя ее координату, мы неизбежно воздействуем на частицу и изменяем ее импульс. Гейзенберг показал, что в одномерном случае произведение неопределенностей в координате и импульсе есть величина, приблизительно равная h/2π. В трехмерном случае

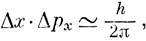
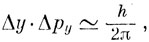
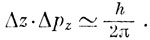
Если определяется точно импульс электрона (и тем самым дебройлевская длина волны электрона), то его координата остается неопределенной, и волновая функция представляет собой плоскую волну в пространстве. Если определяется точно координата электрона, то будет неопределенным импульс, так что волновая функция должна быть суперпозицией волн со всевозможными значениями λ = h/p, которые, интерферируя, усиливаются в одной точке (где находится электрон) и гасятся во всех остальных точках пространства.

В последующих двух главах исследуются решения уравнения (1.12) для относительно простых случаев: электрон в поле постоянного потенциала и электрон в сферически симметричном кулоновском поле (атом водорода). На этих примерах будут проиллюстрированы основные свойства квантовомеханических систем. Прежде чем обсуждать более сложные и тонкие вопросы теории валентности (гл. 7-18), рассмотрим в гл. 6 более детально фундаментальные положения квантовой механики.