7.2. Приближение Борна - Оппенгеймера

Гамильтониан для системы ядер (обозначаемых здесь греческими буквами (μ, ν ...) с координатами X и электронов (обозначаемых латинскими буквами i, j, k ...) с координатами х имеет следующий вид:

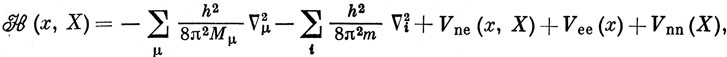
где V_ee, например, представляет собой межэлектронное отталкивание:

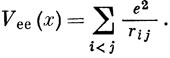
Если выделить кинетическую энергию ядер,

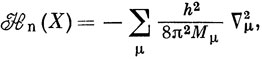
то разность

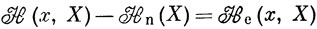
представляет собой гамильтониан, описывающий движение электронов при фиксированных ядрах. Заметим, что H_e зависит только от координат, но не от импульсов ядер.

Предположим теперь, что полная волновая функция, являющаяся решением уравнения

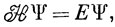
может быть представлена в виде

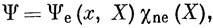
где "электронная" волновая функция удовлетворяет уравнению

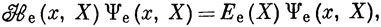
а ядерная волновая функция - уравнению

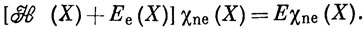
Система этих двух уравнений соответствует приближению Борна - Оппенгеймера ^*).

^*) (Такое приближение часто называют также адиабатическим приближением. - Прим. перев.)

Каков же смысл этих уравнений? Прежде всего в них содержится предположение, что полная волновая функция молекулы может быть представлена в виде произведения электронной функции на ядерную. Электронная волновая функция получается при решении уравнения (7.13) для различных конфигураций ядер. Это дает также электронную энергию Е_е, которую для двухатомной молекулы (X в этом случае есть межъядерное расстояние) можно представить графически, как это сделано на рис. 5.1. Эта электронная энергия рассматривается далее в качестве потенциальной энергии в уравнении, определяющем движение ядер, так что уравнение Шредингера имеет вид (7.14). Его решения χ_ne (X) не зависят от электронных координат, но зависят от характера электронного состояния, так как последнее определяет форму потенциальных кривых. Каждому электронному состоянию Ψ_е соответствует свой набор ядерных волновых функций.

Электронная энергия не является наблюдаемой величиной, хотя и может быть вычислена. Обычно полную энергию представляют в виде суммы электронной энергии, вычисленной при равновесной конфигурации ядер, и ядерной энергии

Таким образом, электронная и ядерная энергии могут быть разделены в выражении для полной энергии.

Спектроскопия дает убедительное подтверждение того, что в общем приближение Борна - Оппенгеймера является достаточно хорошим. В инфракрасных спектрах наблюдаются переходы между различными колебательными уровнями основного электронного состояния; соответствующая картина колебательного спектра может быть выражена через волновые функции χ_ne и энергии Е_n, определенные выше. В видимой и ультрафиолетовой областях спектра наблюдаются переходы между различными электронными уровнями, так что результирующий спектр содержит структуры, возникающие из различных колебательных компонент рассматриваемых электронных состояний. Расположение этих колебательных структур и относительные интенсивности их отдельных компонент могут быть объяснены также на основе рассмотренных выше уравнений.

Теперь обсудим условия, при которых справедливо приближение Борна - Оппенгеймера. Подставляя уравнения (7.10) и (7.12) в уравнение (7.11), можно получить

Оператор H_e содержит дифференцирование только по электронным координатам х и поэтому, используя уравнение (7.13), можно написать

Оператор H_n - оператор дифференцирования по ядерным координатам X, от которых зависит как χ_ne, так и Ψ_e; следовательно, применяя выражение (7.9), получим

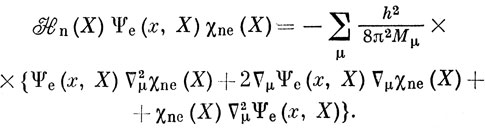
Подставляя уравнения (7.17) и (7.18) в уравнение (7.16)" мы приходим к уравнению (7.14) для ядерной волновой функции, если можно пренебречь членами ∇_μΨ_e и ∇_μ²Ψ_е в уравнении (7.18). Иначе говоря, приближение Борна - Оппенгеймера справедливо, если электронная волновая функция Ψ_e есть медленно меняющаяся функция ядерных координат. Единственный случай, когда приближение Борна - Оппенгеймера, по-видимому, непригодно - это наличие вырожденных или почти вырожденных электронных состояний. В таких случаях члены ∇_μΨ_e, которыми пренебрегают в приближении Борна - Оппенгеймера, приведут к заметному взаимодействию между двумя вырожденными или почти вырожденными электронными состояниями, и только одна волновая функция типа (7.12) не даст хорошего описания системы.

В этой книге рассматриваются методы вычисления только электронной волновой функции Ψ_е и электронной энергии Е_е. По этой причине в дальнейшем под волновой функцией, энергией или гамильтонианом мы будем подразумевать соответствующие электронные величины, хотя и не будем писать в каждом случае значок "е".