Глава 7. Волновые функции многоэлектронных систем

7.1. Свойство антисимметрии

Для многоэлектронной системы члены

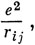
учитывающие отталкивание электронов, должны быть включены в волновое уравнение как часть потенциальной энергии. Тогда электронная волновая функция зависит от координат всех электронов. Если бы не учитывались члены, описывающие электронное отталкивание, то волновое уравнение можно было бы решать, представив многоэлектронную волновую функцию в виде произведения одноэлектронных функций:

Тогда волновое уравнение распалось бы на систему уравнений, каждое из которых содержит координаты только одного электрона, и решениями этих уравнений были бы функции ψ. Однако это невозможно из-за электронного отталкивания, и поэтому точное решение волнового уравнения для многоэлектронной системы не было получено. Это является особенностью не только квантовой механики: многочастичная задача не решена и в классической механике.

Поскольку очень трудно табулировать функции многих переменных и работать с ними, нет другого выбора, как рассматривать многоэлектронные системы, используя функции типа (7.1), и строить их таким образом, чтобы по возможности они были близки к точным решениям волнового уравнения, например, пользуясь вариационным принципом. Только при использовании функций, подобных функциям (7.1), можно построить орбиталь, так как, по определению, орбиталь есть одноэлектронная волновая функция.

Способ получения наилучших атомных орбиталей по методу самосогласованного поля рассматривался в общих чертах в гл. 4. Аналогичную методику можно использовать при построении молекулярных орбиталей; этот вопрос будет обсуждаться в гл. 10.

Рассмотрим набор атомных или молекулярных орбиталей ψ. Поместим на эти орбитали электроны и свяжем с каждой из орбиталей определенный спин. Как уже говорилось в гл. 4, существует два различных спиновых состояния электрона

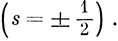
Обозначим спиновые волновые функции этих двух состояний через α и β, соответственно для

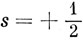
и

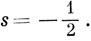
Функция, представляющая собой произведение пространственной части на спиновую, называется спин-орбиталью. Например, полная волновая функция электрона, находящегося на 1s-орбитали, может быть 1sα или 1sβ. Для краткости будем записывать иногда эти спин-орбитали в виде 1s и 1s соответственно, если необходимо указать значение спина электрона.

Волновую функцию многоэлектронной системы можно представить в виде

где первому электрону приписывается спин-орбиталь ψ_a, второму - ψ_b и т. д. ^*). Однако электроны невозможно отличить один от другого, и поэтому наряду с функцией (7.2) можно написать с равным правом функцию

или любую из n! функций, которые можно получить, переставляя n электронов на этих спин-орбиталях. Наиболее общая волновая функция будет линейной комбинацией n! таких функций, в которую все они входят с одинаковым весом. Оказывается, что только одна линейная комбинация дает результаты, согласующиеся с экспериментом, а именно такая комбинация, которая изменяет знак при перестановке координат двух любых электронов. Говорят, что волновая функция антисимметрична по отношению к перестановке двух любых электронов. Например, для системы из двух электронов этому условию удовлетворяет функция

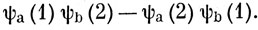
^*) (Например, для основного состояния атома Be это отвечало бы 1s(l) 1s‾ (2) 2s (3) 2s‾ (4).)

В общем же случае свойством антисимметричности обладает волновая функция, записанная в виде определителя

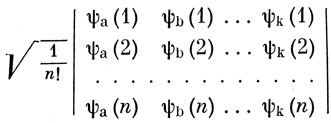
Действительно, перестановка координат двух электронов эквивалентна перестановке соответствующих строк в определителе, что приводит к изменению знака функции. Вместе с нормировочным множителем 1/√n! функция вида (7.5) называется слэтеровским определителем. Полная запись функции типа (7.5) довольно громоздка; сокращенно ее будем представлять в виде

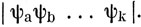
Волновая функция такого вида удовлетворяет принципу Паули. Действительно, если два электрона в одном атоме имеют четыре одинаковых квантовых числа, то в волновой функции будут две одинаковые спин-орбитали. Это означает, что два столбца определителя (7.5) совпадают, и он, следовательно, обращается в нуль; другими словами, такой волновой функции не может существовать.

Было найдено, что свойством антисимметричности обладают не только волновые функции для электронов, но также функции многих других элементарных частиц, и прежде всего протонов и нейтронов. Например, именно это обстоятельство в применении к системе протонов приводит к существованию двух видов Н₂ - орто- и пара-водорода; однако этот вопрос лучше обсудить в другом месте, а не в этой книге.