Глава 8. Симметрия

8.1. Введение в теорию групп симметрии

Если молекула обладает какой-либо симметрией, то можно получить некоторые сведения о характере ее волновых функций, не решая волнового уравнения. Поясним это на примере формальдегида.

Допустим, что нужно построить молекулярные орбитали для формальдегида при равновесной конфигурации ядер. Если электрон находится на орбитали ψ, то плотность вероятности его нахождения в некоторой точке пространства равна значению ψ² в этой точке. Пусть произвольная точка пространства (отмеченная цифрой 1 на рис. 8.1) определена радиусом-вектором rr и расположена над плоскостью молекулы. Плотность вероятности нахождения электрона в этой точке равна ψ²(r₁). Однако существуют в пространстве еще три точки (отмеченные на рис. 8.1 цифрами 2, 3, 4), которые полностью эквивалентны выбранной. Например, точка 2 расположена под плоскостью молекулы, но на тех же расстояниях от каждого из ядер, что и точка 1. Очевидно, что плотность вероятности в точках 1 и 2 должна быть одинаковой, т. е. ψ²(r₁) = ψ²(r₂). Этому условию можно удовлетворить двумя способами: или ψ(r₁) = ψ(r₂), или ψ(r₁) = -ψ(r₂). Таким образом, волновая функция либо симметрична по отношению к замене точки 1 точкой 2, либо антисимметрична относительно такой замены.

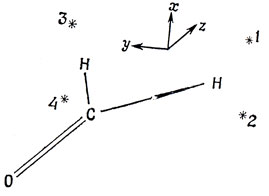
Рис. 8.1. Точки, эквивалентные по отношению к ядрам молекулы формальдегида. Точки с номерами 1 и 3 расположены над плоскостью молекулы, а с номерами 2 и 4 - под ней

Точки 1 и 2 переводятся друг в друга при операциях симметрии, сохраняющих неизменной конфигурацию ядер. В общем случае операция симметрии есть такое перемещение тела, которое переводит его в эквивалентное положение, так что после этого перемещения каждая точка тела совпадает с точкой, эквивалентной ей в первоначальном положении тела (или, в частности, остается неизменной). Иначе говоря, если мы видим тело до и после такой операции, но не во время ее действия, то совершенно невозможно сказать, выполнена ли была операция симметрии или нет.

Если осуществляется поворот на 180° вокруг оси z, то в молекуле формальдегида точки 1 и 4, 2 и 3 переходят друг в друга, но конечное расположение молекулы будет эквивалентно исходному. Аналогично при отражении в плоскости yz, в которой расположены ядра, меняются местами точки 1 и 2, 3 и 4, однако после отражения снова имеем эквивалентную ориентацию молекулы. Наконец, операцией симметрии для молекулы формальдегида является также отражение в плоскости xz, при котором переходят друг в друга эквивалентные точки 1 и 3, 2 и 4.

Таким образом, рассматриваемую молекулу можно перевести в эквивалентное положение в результате одной из трех операций симметрии: двух отражений и поворота. Операции симметрии составляют предмет специальной области математики - теории групп. В любом случае должен быть элемент, играющий роль числа 1 в обычной алгебре, т. е. при умножении его на функцию последняя остается неизменной. Например, в матричной алгебре таким элементом является единичная матрица. В теории групп этот элемент называется тождественным преобразованием. Для групп симметрии тождественное преобразование есть такая операция симметрии, при которой тело остается неподвижным. В рассматриваемом примере молекулы формальдегида (см. рис. 8.1) тождественное преобразование, поворот и два отражения образуют совокупность операций, которую называют точечной группой симметрии молекулы.

Согласно общему определению, группа есть совокупность элементов, связанных между собой в соответствии с некоторыми правилами. Для того чтобы получить формальные результаты теории групп, нет необходимости уточнять, приписываем ли мы элементам групп какой-либо физический смысл или нет. Хотя в этой книге придется иметь дело лишь с группами, образованными операциями симметрии, целесообразно начать с некоторых основных определений и теорем, которые применимы к любой группе.

1. Число элементов группы называют порядком группы (его принято обозначать буквой h).

2. Произведение двух любых элементов группы, в частности квадрат любого из элементов, также является элементом группы. Таким образом, АВ = С, где А, В и С - элементы группы. Однако элементы группы не всегда коммутируют, так что АВ и В А могут и не совпадать. Мы не будем более строго определять произведение двух элементов группы до тех пор, пока не придадим элементам группы конкретный смысл.

3. Один из элементов группы является единичным. Обозначим его буквой I, хотя чаще используют обозначение Е. Для любого элемента группы А имеет место равенство IA = AI = А.

4. Выполняется ассоциативный закон умножения, т. е. произведение ABC не зависит от того, как объединены сомножители: А(ВС) = (АВ)С.

5. Каждый элемент имеет обратный ему элемент, который также является элементом группы. Элемент В называется обратным по отношению к элементу А, если ВА = АВ = I. Можно записать это так: В = А^-1.

6. В любой группе имеются подгруппы меньшего порядка, для которых выполнены условия 2-5 (очевидно, например, что I - подгруппа первого порядка). Можно показать, что порядок подгруппы является делителем порядка полной группы. Например, группа порядка 6 может иметь подгруппы только порядков 1, 2, 3.

7. Если А и X - элементы группы, то Х^-1 АХ - также элемент группы, например В.

Говорят, что элемент В получается из A с помощью преобразования подобия с элементом X, а элемент В называют сопряженным элементу А. Заметим, что, умножая обе части уравнения (8.1) слева на X, а справа на X^-1, получаем

Но XX^-1 = 1, и если обратным элементу X является элемент Y, то

Другими словами, свойство сопряженности элементов А и В является взаимным. Полная совокупность взаимно сопряженных элементов называется классом. Например, если каждый из элементов Х^-1АХ, Х^-1ВХ и Х^-1СХ равен одному из элементов А, В или С для произвольного элемента X, то говорят, что элементы А, В и С образуют класс. Число элементов в классе должно быть делителем порядка группы, но совсем не обязательно, чтобы каждому такому делителю соответствовал какой-либо класс. В группе шестого порядка, например, классы могут содержать 1, 2 или 3 элемента.

Вернемся теперь к обсуждению групп симметрии и выясним прежде всего, какие операции симметрии вообще возможны. С тремя из них мы уже познакомились: тождественное преобразование, поворот вокруг оси и отражение в плоскости. Нам встретятся еще два преобразования симметрии: инверсия в центре симметрии (при этой операции точка с координатами x, y, z переходит в точку с координатами -x, -y, -z) и поворот вокруг оси с последующим отражением в плоскости, перпендикулярной к этой оси. В табл. 8.1 приведены общепринятые обозначения для этих операций симметрии.

Таблица 8.1. Обозначения операций групп симметрии^*

^*) (Мы будем иметь дело лишь с так называемыми точечными группами симметрии, возможные элементы которых перечислены в этой таблице. Существуют также группы симметрии, элементами которых являются трансляции; их называют пространственными группами. Они важны при изучении кристаллов.)

На рис. 8.2 показаны операции симметрии молекулы формальдегида: I, С₂(z), σ_υ(xz), σ_υ'(yz). Совокупность этих операций образует группу симметрии, которую называют С_2υ. Убедимся сначала, что они действительно образуют группу, т. е. удовлетворяют основным групповым законам, перечисленным выше.

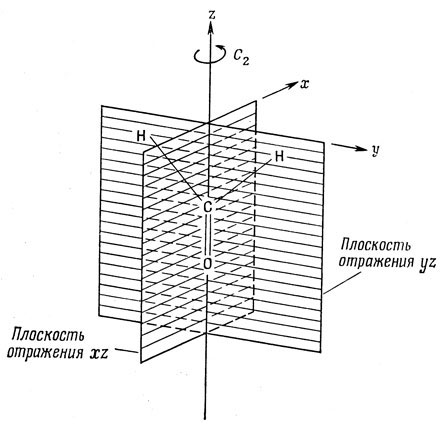
Рис. 8.2. Операции симметрии молекулы формальдегида

Проверим сначала, что произведение двух любых преобразований группы симметрии есть элемент этой же группы. Результаты перемножения элементов группы приведены в табл. 8.2, которая называется таблицей группового умножения.

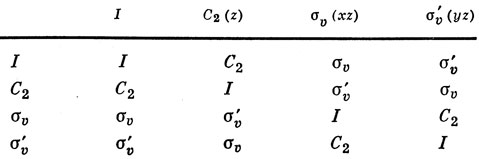
Таблица 8.2. Таблица группового умножения для группы C_2υ

Например (см. рис. 8.2), применение сначала операции отражения σ_υ(xz), а затем σ_υэ(yz) эквивалентно одной операции С₂. В алгебраической форме это записывается так: σ_υ' σ_υ = С₂, а в табл. 8.2 элементом, стоящим на пересечении столбца σ_υ и строки σ_υ', является С₂. Для рассматриваемой группы произведение двух любых элементов не зависит от порядка сомножителей, т. е. операции группы коммутируют. Такая группа называется абелевой. Если среди элементов группы симметрии молекулы нет осей вращения порядка выше второго, то такая группа всегда является абелевой. Из табл. 8.2 видно также, что, так как на главной диагонали стоит элемент I, каждый из элементов группы равен своему обратному. Операции I и С₂ образуют подгруппу второго порядка, однако I, σ_υ и σ'_υ не образуют подгруппы, потому что σ_υσ'_υ = С₂.

Поскольку все элементы рассматриваемой группы коммутируют, имеем

так что каждый элемент образует класс. Это является общим свойством абелевых групп.

Рассмотрим теперь неабелеву группу С_3υ, которая является группой симметрии молекулы NH₃. Как видно из рис. 8.3, операции симметрии таковы: тождественное преобразование, повороты на угол 2π/3(С₃) и 4π/3(С₃²), а также отражения в трех вертикальных плоскостях симметрии, каждая из которых содержит один из атомов водорода. Обозначим атомы водорода буквами a, b и с, а отражения в трех плоскостях - соответственно σ_υa, σ_υb и σ_υc. На рис. 8.3 показан результат последовательного применения к молекуле операций С₃ и σ_υa. Окончательные положения атомов a, b и с зависят от того, в какой последовательности выполняются эти операции: σ_υaC₃ = σ_υb; C₃σ_υa = σ_υc.

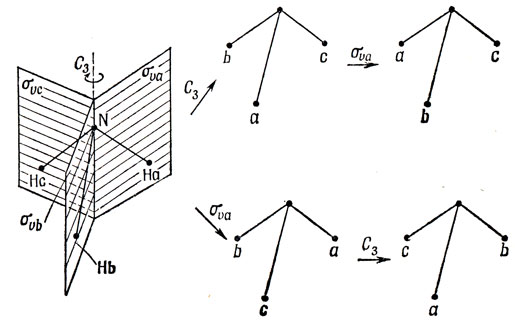
Рис. 8.3. Результат последовательного применения операций вращения и отражения к молекуле, обладающей симметрией С_3υ

Таблица 8.3. Таблица группового умножения для группы C_3υ

Из этой таблицы видно, что каждое отражение совпадает с обратным ему элементом, но для С₃² обратной операцией является С₃, и наоборот. Элементы I, С₃ и С₃² образуют подгруппу порядка 3.

Можно показать, что группа С_3υ разбивается на три класса: единичный элемент, С₃ и С₃², а также класс, состоящий из отражений σ_υa, σ_υb и σ_υc. Докажем, что, например, повороты С₃ и С₃² образуют класс, рассматривая преобразования подобия их (8.1) со всеми элементами группы.

Аналогично, применяя к элементу С₃² преобразование подобия с элементами I, С₃ и С₃², получим С₃², а с элементами σ_υa, σ_υb и σ_υc - С₃. Итак, элементы С₃ и С₃² действительно образуют класс. Действуя таким образом, можно показать, что три отражения σ_υa, σ_υb, σ_υc также образуют класс. Следовательно, элементы трех различных классов группы симметрии С_3υ - это преобразования трех различных типов, и этот результат является общим правилом. Две операции принадлежат к одному и тому же классу в том случае, если одна из них сводится к другой в новой системе координат, которая может быть получена преобразованием симметрии.

Первый шаг на пути применения теории групп симметрии в молекулярных задачах - установление группы симметрии молекулы. При этом целесообразно руководствоваться следующими правилами:

1. Существуют три группы симметрии, имеющие несколько осей симметрии высших порядков: группа тетраэдра T_d (например, молекула СН₄), группа октаэдра O_h (молекула SF₆) и группа икосаэдра I_h (к которой относятся некоторые соединения бора).

2. Если молекула не относится ни к одной из этих трех групп симметрии, то сначала нужно определить, какие оси симметрии возможны. Если их нет вообще, но молекула имеет плоскость симметрии, то группой симметрии молекулы является группа С_s (например, хинолин).

3. Если молекула имеет одну или несколько осей симметрии, то группа симметрии обозначается С_n, где n - наивысший возможный порядок оси симметрии (порядок главной оси). Может и не быть главной оси, а вместо этого три взаимно перпендикулярные оси второго порядка С₂ (например, как в нафталине). В этом случае любую из этих осей можно выбрать в качестве главной оси симметрии.

4. Если молекула имеет операцию симметрии S_n (см. табл. 8.1), где n равно удвоенному порядку главной оси, но в группе симметрии не содержится никаких других операций симметрии, кроме, может быть, инверсии, то группа симметрии молекулы есть S_n (например, группа S₄ молекулы тетрафенилметана).

5. Далее следует выяснить, имеется ли n осей симметрии второго порядка, перпендикулярных к главной оси порядка n. Если они есть, это группа типа D, если нет, - группа типа С.

6. С-Группы бывают трех видов: С_n, не имеющая вообще плоскостей симметрии (к группе С₁ относится любая молекула, не обладающая никакой симметрией); C_nυ, характеризующаяся вертикальной плоскостью симметрии (например, группа C_3υ аммиака); C_nh, содержащая горизонтальную плоскость симметрии (например, группа C_2h транс-дибромэтилена).

7. D-Группы также бывают трех видов: D_n, не имеющая плоскостей симметрии (например, группа D₂ скрученной молекулы этилена); D_nh, характеризующаяся горизонтальной плоскостью симметрии (например, группа D_6h бензола); D_nd, не содержащая горизонтальной плоскости симметрии, но включающая n диагональных плоскостей (например, группа аллена D_2d),

8. Для линейных молекул прямая, на которой расположены ядра, является осью вращения бесконечного порядка. Такие молекулы принадлежат к бесконечным группам, которые бывают двух типов: С_∞υ (при отсутствии горизонтальной плоскости симметрии, например, как у молекулы HCl) и D_∞h (при наличии такой плоскости, например, как у молекулы CO₂).

На рис. 8.4 приведен пример применения перечисленных выше правил (определена группа симметрии молекулы аллена). Решая задачу 8.1, можно приобрести некоторый навык в определении группы симметрии молекул.

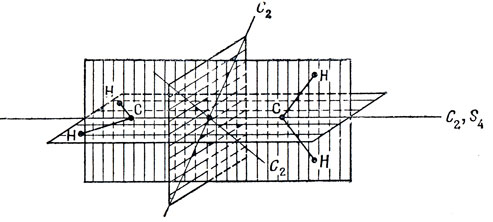
Рис. 8.4. Операции симметрии для молекулы аллена, имеющей группу симметрии D_2d