8.2. Представления групп

В начале этой главы уже говорилось, что молекулярная орбиталь формальдегида или должна оставаться неизменной, или менять знак при действии на нее операций симметрии группы С_2υ. Применяя операторные обозначения (см. разд. 6.1), можно написать, например,

так что ψ является собственной функцией оператора С₂ с собственным значением ±1. Если имеется МО, для которой

Iψ = + 1·ψ    συ = + 1·ψ,
С2ψ = + 1·ψ    συ' = + 1·ψ,

то набор из четырех чисел +1, +1, +1, +1 характеризует симметрию орбитали, и в этом случае говорят, что орбиталь полностью симметрична.

Симметрия других орбиталей определяется иными наборами чисел. Однако правила группового умножения (см. табл. 8.2) налагают некоторые ограничения на эти наборы и выделяют из них допустимые. Например, поскольку σ_υ'σ_υ = С₂, то, если орбиталь симметрична по отношению к σ_υ и антисимметрична относительно σ_υ', она должна быть антисимметрична по отношению к С₂. Таким образом, возможны только четыре набора чисел, которые соответствуют таблице группового умножения для группы С_2υ, при условии, что оператор I имеет собственное значение +1. Эти наборы приведены в табл. 8.4.

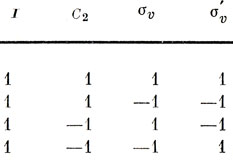
Таблица 8.4. Наборы чисел, удовлетворяющие таблице группового умножения для группы C_2υ

Однако наряду с этими наборами чисел существуют также и наборы матриц, удовлетворяющие таблице группового умножения ^*). Два таких набора приведены ниже:

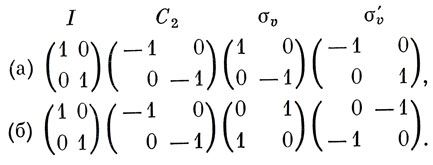
^*) (Для полного понимания материала, изложенного в настоящей главе, требуются элементарные сведения из матричной алгебры. Прежде всего надо знать правило умножения матриц. Если С = АВ, то элемент r-й строки и s-го столбца матрицы С определяется так: c_rs = ∑_ta_rtb_ts, где суммирование проводится по всем столбцам матрицы А и строкам матрицы В.)

Легко проверить, что матрицы каждого из наборов удовлетворяют правилам умножения в группе. Например,

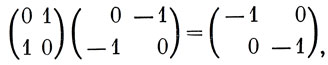
что соответствует условию σ_υσ_υ' = С₂.

Всякую совокупность матриц, которые перемножаются в соответствии с таблицей группового умножения, называют представлением группы. Частным случаем матриц являются числа, приведенные в табл. 8.4 и дающие одномерное представление группы.

Представления группы - это наборы матриц, которые показывают, как при операциях группы преобразуются функции (или их совокупность). Например, при действии всеми операциями группы на полносимметричную функцию получаем представление, состоящее только из чисел +1. Рассмотрим теперь две функции x и y (декартовы координаты, выбранные в соответствии с рис. 8.1): при тождественном преобразовании точка (x, y) остается насесте, при повороте С₂ она переходит в точку (-x, -y); при отражении σ_υ - в точку (x, -y); наконец, при отражении, σ_υ' - в точку (-x, y). Эти преобразования в матричной форме выражаются следующим образом:

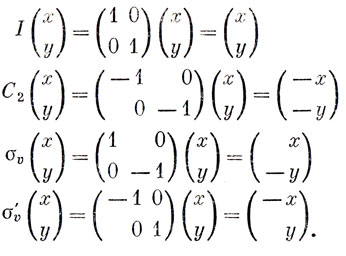
Таким образом, матрицы второго порядка, образующие набор (а), дают представление группы. Говорят, что функции x и y являются базисом представления группы или что функции x и y преобразуются по представлению группы (а).

Очевидно, что число различных представлений группы, которые можно построить, зависит только от нашего умения получать разные наборы функций, образующие базисы. Любая совокупность функций f₁ ... f_n, которые при операциях группы переходят в функции f₁' ... f_n', являющиеся линейными комбинациями исходных функций, образует базис представления группы. Это очень важная теорема, к которой мы еще вернемся в следующем разделе.

Хотя каждая группа имеет бесчисленное множество представлений, среди них существует конечное число представлений, которые называются неприводимыми представлениями. Этот термин будет довольно часто употребляться в дальнейшем, так что удобно использовать сокращенное обозначение НП. Мы увидим позднее, что весьма полезно провести аналогию между представлением и вектором. В конечном пространстве можно построить бесчисленное множество векторов, однако ортогональных единичных векторов будет конечное число. Аналогично у конечной группы существует бесконечное число представлений, но конечное число НП. Подобно тому как произвольный вектор можно выразить через базисные ортогональные единичные векторы (коэффициентами являются соответствующие компоненты), так и любое представление группы можно выразить через НП.

Для разложения представления на неприводимые используется преобразование подобия [см. соотношение (8.1)]. Пусть имеется набор матриц А, В, С, ..., которые дают представление группы. Представление называется приводимым, если существует такое преобразование подобия с матрицей X, которое преобразует исходные матрицы в блочные матрицы следующей структуры: на диагонали расположены субматрицы меньшего порядка, чем исходные, а все остальные элементы - нули.

Например,

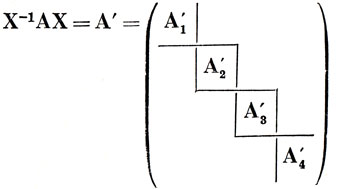
Субматрицы А_k', В_k', C_k', ... должны иметь один и тот же порядок, а матрицы А₁', А₂', ... могут иметь различные порядки.

Допустим, что в соответствии с таблицей группового умножения

Тогда

следовательно,

Но из правила перемножения матриц вытекает, что

поэтому всякий набор субматриц A_k'B_k', C_k', ... подчиняется таблице группового умножения, и поэтому такие наборы образуют представления группы.

Если невозможно найти такое преобразование подобия, которое приводит все матрицы представления к виду (8.4), то представление называют неприводимым. Любое представление группы можно разложить на неприводимые представления этой группы.

Теперь сформулируем (без доказательства) некоторые важные свойства НП группы ^*).

^*) (Строгое доказательство перечисленных свойств НП можно найти лишь в полных курсах по теории групп (см., например, [24]). В книге [11] ясно излагаются сами свойства, но не даются полные доказательства.)

1. Сумма квадратов размерностей НП равна порядку h группы.

2. Сумма квадратов характеров матриц в любом НП равна h. Характером (или следом) матрицы называется сумма ее диагональных элементов; он обозначается буквой χ. Таким образом,

где i - номер НП и χ(R) - характер, соответствующий преобразованию симметрии R.

3. Характеры НП можно рассматривать как компоненты векторов в пространстве h измерений. Векторы, соответствующие двум различным НП, ортогональны ^*). Учитывая также равенство (8.9), получаем

^*) (В более общем случае, если Г_mnⁱ (R) - элемент m-й строки, n-го столбца матрицы i-го НП, то совокупность их для всех операций R подобна компонентам полного набора ортогональных векторов в пространстве h измерений. Однако в дальнейшем этот более общий результат не используется.)

4. Следы матриц, относящихся к операциям одного и того же класса, одинаковы для всех матриц данного представления.

5. Число НП группы равно числу классов группы.

В качестве первого примера рассмотрим группу С_2υ. В ней содержится четыре элемента и четыре класса, а следовательно, четыре одномерных НП. Наборы чисел, удовлетворяющих таблице группового умножения, приведены в табл. 8.4. Эти числа, являющиеся одновременно характерами НП, если их рассматривать как матрицы первого порядка, помещены в таблице характеров НП группы С_2υ (см. табл. 8.5).

Таблица 8.5. Таблица характеров группы C_2υ

Каждое НП обозначается символом, приведенным слева в табл. 8.5. Эти обозначения являются стандартными и вводятся в соответствии со следующими правилами:

1. Буквами А и В обозначаются одномерные НП; Е - двумерные; Т - трехмерные (иногда последние обозначают также буквой F).

2. Представления, характеры которых равны +1 для поворотов вокруг главной оси на угол 2π/n, обозначаются буквой А, а представления, для которых эти характеры равны -1, обозначаются буквой В.

3. Если молекула обладает центром симметрии, то индексы g и u указывают на симметрию по отношению к инверсии в центре: для g-представлений характер операций инверсии равен +1; для u-представлений равен -1.

4. Всегда существует одно НП, характеры которого равны +1 для всех операций. Оно называется полносимметричным НП и обозначается буквой A (A_g - при наличии центра симметрии); если в группе имеется несколько представлений типа A, то они обозначаются A₁, А' или A_1g.

В таблице характеров часто указывают также простейшие функции, образующие базис НП. Например, координаты z, x, y, xy (система координат введена согласно рис. 8.1) образуют базисы неприводимых представлений А₁, В₁, В₂, А₂ соответственно для группы С_2υ.

Вернемся теперь к рассмотрению группы С_3υ с таблицей группового умножения 8.3. Порядок этой группы равен 6, она состоит из трех классов. Поэтому должны быть три НП - два одномерных и одно двумерное: 1² + 1² + 2² = 6.

Эти три НП рассмотрены ниже (убедитесь на этом примере, что результат, сформулированный в примечании на стр. 134, справедлив):

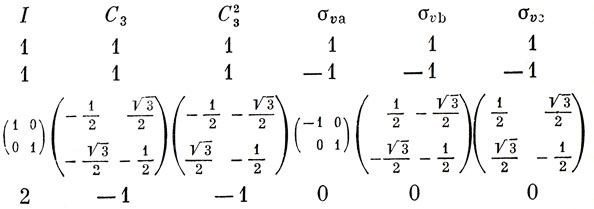
В последней строке содержатся характеры двумерного представления. Отметим, что правила 3 и 4, упоминавшиеся на стр. 134, выполняются для характеров всех трех неприводимых представлений, как в этом легко убедиться. В таблице характеров группы приводят характеры лишь для операций разных классов, как это сделано в табл. 8.6.

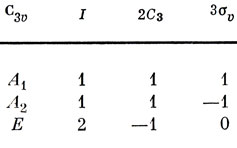
Таблица 8.6. Таблица характеров группы С_3υ

Здесь не приводятся таблицы характеров тех групп симметрии, которые не упоминаются в этой книге. В списке литературы к настоящей главе даны ссылки на книги, в которых имеются таблицы характеров для всех известных групп симметрии.