8.3. Применения теории групп в задачах теории валентности

В начале этой главы было выяснено, что МО для формальдегида должны преобразовываться определенным образом при действии на них операций группы симметрии ядерного остова, так чтобы электронная плотность в эквивалентных точках молекулы была одинакова. Теперь рассмотрим более подробно свойства симметрии волновых функций и покажем, как результаты, полученные в предыдущих разделах, можно использовать для упрощения задач теории валентности.

Прежде всего, что подразумевается под операциями симметрии молекулы? До сих пор рассматривались операции симметрии таким образом, как если бы молекула была твердым телом или даже просто набором точек пространства. На самом деле молекула не является ни тем ни другим, а представляет собой совокупность электронов и ядер, положения которых в пространстве можно описывать только с помощью плотностей вероятности. Симметрия волновой функции должна определяться на основе симметрии гамильтониана, для которого волновая функция является собственной. Другими словами, симметрия волновой функции характеризуется теми операциями симметрии, которые оставляют электронный гамильтониан неизменным.

Выясним это снова на примере формальдегида. Электронные волновые функции определены в приближении Борна - Оппенгеймера (разд. 7.2), т. е. при фиксированных положениях ядер. Если ядра рассматриваются в их равновесной конфигурации, то перестановка двух протонов не изменяет потенциального поля, действующего на электроны, т. е. электронный гамильтониан не изменяется при такой перестановке. В общем случае любая операция симметрии остова, образованного ядрами, не меняет электронный гамильтониан. Если H инвариантен относительно операции симметрии R, то H и R коммутируют. Отсюда следует, что если Ψ есть собственная функция оператора H,

то

так что

Другими словами, функция Ψ_k = RΨ_k есть также собственная функция оператора H c тем же самым собственным значением, что и функция Ψ_k. Но известно, что это возможно только в том случае, если Ψ_k' - линейная комбинация функций, соответствующих вырожденному состоянию с энергией E_k. Если же состояние с энергией E_k невырождено, то для нормированных функций Ψ_k' = ±Ψ_k. Таким образом, действие операции R на любую из функций набора, соответствующего вырожденному состоянию, преобразует каждую из этих функций в их линейную комбинацию, так что собственные функции, отвечающие данному вырожденному состоянию, образуют базис представления группы. Точнее говоря, набор этих функций образует базис НП группы. Если бы это было не так, то можно было бы из функций данного набора построить такие комбинации их, которые образовывали бы малые поднаборы, являющиеся базисами НП группы. Но тогда было бы не ясно (по крайней мере из требования симметрии), почему функции различных поднаборов относятся к одному и тому же вырожденному состоянию. Другими словами, если нет вырождения, не связанного со свойствами симметрии гамильтониана (случайного вырождения), то функции вырожденного состояния образуют базис НП группы симметрии. Иначе это можно выразить так: все собственные функции, соответствующие одной и той же энергии, преобразуются по НП группы симметрии.

В качестве примера рассмотрим две волновые функции молекулы, обладающей симметрией C_3υ (см. рис. 8.5). Коэффициенты, отмеченные на рисунке, обозначают веса волновых функций, отнесенных к каждой из трех эквивалентных точек молекулы. Нетрудно заметить, что вращения на угол 2π/3 или 4π/3 переводят каждую из этих функций в линейную комбинацию функций (а) и (b). Если функции (а) и (b) соответствуют вырожденному состоянию, то их линейные комбинации также являются собственными функциями этого состояния и по отношению к операциям вращения из группы С_3υ они удовлетворяют требованиям симметрии. Можно показать, что это выполняется и для любой другой операции, т. е. они образуют базис представления группы. Из рассмотрения характеров вытекает, что это представление является НП типа Е; мы вернемся еще к нему позднее.

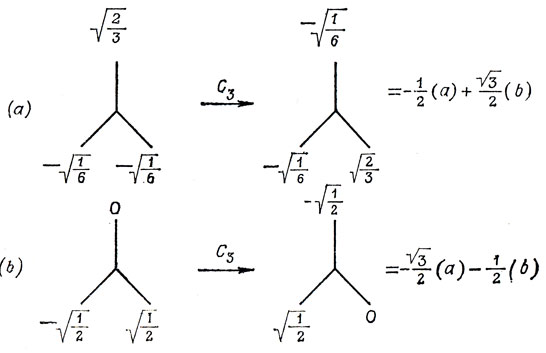
Рис. 8.5. Действие операции поворота на две функции, образующие базис представления Е группы С_3υ

Этот результат находит важные применения при построении молекулярных волновых функций. В гл. 6 отмечалось, что, когда невозможно получить точное решение уравнения Шредингера, как это имеет место для всех многоэлектронных систем, обычно строят приближенное решение в виде разложения по системе функций, образующих полную систему. Поскольку собственные функции гамильтониана преобразуются по НП группы симметрии, функции, по которым производится разложение, удобно брать в такой форме, чтобы они тоже преобразовывались по НП группы. Тогда приближенные решения являются такими линейными комбинациями базисных функций, которые преобразуются по тому же НП, что и точные собственные функции гамильтониана. Этот результат будет использован при построении МО для молекулы Н₂O (гл. 12) и октаэдрического комплекса (гл. 13).

Чтобы применять описанный выше способ, необходимо выяснить, по каким НП преобразуются отдельные элементы исходного набора, или, если они вообще в отдельности не являются базисами НП группы, построить такие их комбинации, которые являются базисами. Это не всегда просто. Рассмотрим теперь методику такого построения.

Будем исходить из набора функций, которые преобразуются друг через друга при операциях группы. Они образуют базис представления группы. Найдем разложение этого представления на неприводимые. Для этого, к счастью, достаточно знать только характеры представления, а не сами матрицы, дающие представление и вид приводящей его матрицы. Таким образом, сначала разыщем характеры представления.

Допустим, что две исходные функции f₁ и f₂ при операции из группы симметрии переходят в две другие функции f₁' и f₂', согласно формулам

так что в матричном виде это преобразование записывается в форме

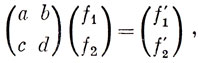
где матрица (_c^a_d^b) является одной из матриц представления группы (эта матрица соответствует операции R), а f₁ и f₂ - функции базиса.

След матрицы равен а + d, причем а характеризует вклад f₁ в f₁' a d - вклад f₂ в f₂', т. е. вклад первоначальных функций в получающиеся после преобразования. Таким образом, для того чтобы определить характер представления, соответствующий какой-либо из операций, необходимо выяснить, каков вес каждой из исходных функций в преобразованной, и полученные результаты сложить.

Возьмем в качестве примера группу С_3υ. Допустим, что строится МО для молекулы NH₃. Сначала построим линейные комбинации водородных 1s-АО, которые преобразуются по НП группы. Обозначим исходные функции через φ_а, φ_b и φ_с (см. рис. 8.3). Чтобы найти характеры представления, для которого φ_а, φ_b и φ_с являются базисными функциями, надо выяснить, какие из этих функций остаются неизменными при данной операции симметрии (поскольку при операции симметрии функции либо сохраняются неизменными, либо переходят в другие функции). При тождественном преобразовании все функции неизменны, при повороте С₃ все три функции изменяются, переходя друг в друга; при каждой операции отражения только одна из функций не изменяется (например, при операции σ_υa функция φ_а остается неизменной, а функции φ_b и φ_c переходят друг в друга). Характеры представления, которое обозначим Г, равны

    I   2С3   3συ 
Г = 3    0     1

В случае если функции не остаются совершенно неизменными или не переходят полностью в другие функции при операциях группы, иногда бывает трудно определить даже характеры представления. В гл. 13 будет получена полезная формула, определяющая характер для произвольной операции вращения при выборе в качестве базисных функций сферических гармоник. Пользуясь этой формулой, можно легко вычислить характер любого представления, для которого базисом является набор АО, центрированных в точке, инвариантной относительно любой операции группы.

Разложим теперь представление Г на НП. Достаточно знать только характеры представления, чтобы это сделать, поскольку след матрицы остается неизменным при преобразовании подобия ^*). Отсюда следует, что характер представления, соответствующий какой-либо операции симметрии R, равен сумме характеров НП, входящих в разложение, для этой операции. Таким образом,

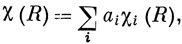
^*) (Это легко можно показать, пользуясь правилами умножения матриц.)

где i - номер НП и a_i показывает, сколько раз каждое из них входит в приводимое представление (это всегда положительное целое число).

Вернемся теперь к рассматриваемой молекуле NH₃. Из табл. 8.6 легко получить, что единственная комбинация характеров НП, дающая характеры представления Г, соответствует разложению Г = A₁ + Е.

В более сложных случаях только из рассмотрения таблицы характеров не удается получить разложение приводимого представления на неприводимые. Для этого существует, однако, простой метод, основанный на том, что характеры НП можно рассматривать как набор ортогональных векторов, с длиной h^1/2 [см. выражение (8.10)]. Беря вектор, задаваемый характерами представления, можно непосредственно найти компоненты ортогональных векторов, которые являются характерами НП, используя закон скалярного умножения векторов. Таким образом, если

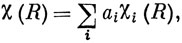
то, умножая обе части равенства на χ_j(R) и суммируя по всем R, имеем

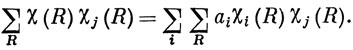
Но, согласно уравнению (8.10),

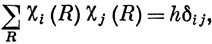
следовательно,

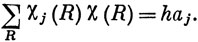
Иначе говоря, если вектор Р задан совокупностью характеров χ(R), а вектор Q_j - совокупностями характеров χ_j(R),

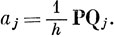
Для рассматриваемого случая

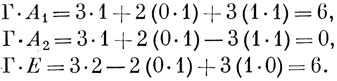
Отсюда получается в соответствии с тем, что имеет место из простого рассмотрения таблицы характеров, что Г = A₁ + Е.

Следующий шаг в проводимом рассмотрении - найти линейные комбинации базисных функций, преобразующиеся по НП группы. В простых случаях это можно сделать на основе таблицы характеров. Например, выясним, какие комбинации водородных 1s-орбиталей формальдегида преобразуются по НП группы С_2υ. Если φ₁ и φ₂ - две АО, то методом, описанным выше, можно легко показать, что эти две функции образуют базис представления, которое раскладывается на сумму НП A₁ и B₂. Поскольку А₁ - полносимметричное представление, то соответствующая ему базисная функция есть φ₁ + φ₂. Для всех операций группы R (φ₁ + φ₂) = + 1·(φ₁ + φ₂). Комбинация, преобразующаяся по B₂, должна быть антисимметрична относительно операций С₂ и σ_υ, поэтому она представляет собой φ₁ - φ₂. Эти две комбинации функций φ₁ и φ₂ называют симметризованными комбинациями.

Общий метод построения функций, преобразующихся по НП группы, заключается в следующем. Берем одну из функций набора φ и применяем к ней по очереди все операции группы, результат действия каждой из операций умножаем на соответствующий характер и все полученные произведения суммируем. Таким образом,

где ψ_t - симметризованная функция, преобразующаяся по представлению с номером t. При таком методе получаются, вообще говоря, ненормированные функции.

Докажем этот результат для невырожденных (одномерных) НП. Всегда можно любую из базисных функций φ выразить через симметризованные функции ψ_s:

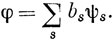
Отсюда следует, что

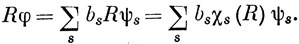
Умножая обе части равенства на χ_t(R) и суммируя по всем R, получаем

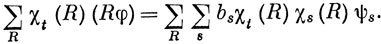
Но из условия ортогональности характеров различных НП следует, что в двойной сумме справа остаются лишь слагаемые, в которых t = s, т. е.

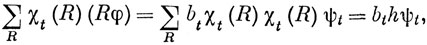
что дает выражение (8.20) без учета нормировки.

Соотношение (8.20) справедливо также для многомерных НП (см. [24]), однако в этом случае, чтобы получить компоненты набора k-кратно вырожденных функций, необходимо выполнить эту процедуру k раз, выбирая различные исходные функции φ. Построенные таким путем k-функции не являются, вообще говоря, взаимно ортогональными, так что затем их следует ортогонализовать.

Чтобы пояснить это на примере, еще раз вернемся к уже рассмотренной молекуле NH₃:

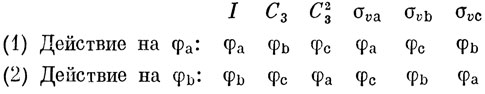
Умножая функции первой строки на соответствующие характеры НП А₁ и складывая, находим

После нормировки получаем симметризованную функцию ^*)

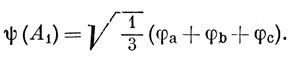
^*) (Здесь нормировочный множитель вычислен без учета перекрывания атомных функций. - Прим. перев.)

Следует заметить, что тот же результат получается, если использовать функции второй строки. Для получения симметризованных функций типа Е нужно построить две компоненты. Умножая первую строку на характеры НП Е и складывая, имеем

что дает после нормирования функции

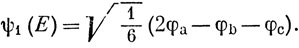
Действуя аналогичным образом с функциями, записанными во второй строке, получим

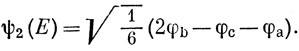
Однако функции ψ₁ и ψ₂ не ортогональны. Для нахождения ортогональных функций можно использовать процедуру Шмидта. Возьмем функции

и найдем с таким образом, чтобы ψ₁ и ψ₂' были ортогональны. Заметим, что

Это условие выполняется, если

В нашем примере

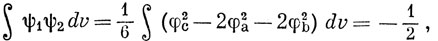
так что

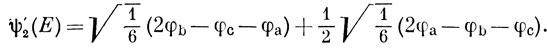
Нормируя функцию, получим

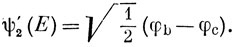
Эти две функции, ψ₁(Е) и ψ₂'(E), как было показано (см. рис. 8.5), являются базисными для представления Е группы С_3υ.

В квантовой механике часто возникает еще одна проблема. Допустим, имеются два набора функций f₁ ... f_m и g₁ ... g_n, причем функции f являются базисными для представления группы с характерами χ_f(R), а функции g образуют базис представления с характерами χ_g(R). Набор функций f_ig_j (их всего m·n штук) должен также образовывать базис представления группы; каковы характеры этого представления?

Поскольку

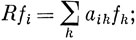
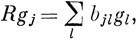
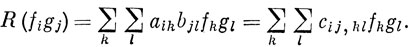
Отсюда следует, что

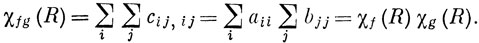
Набор функций fg называется прямым произведением наборов f и g. Характеры представления, по которому преобразуется прямое произведение, равны произведению соответствующих характеров перемножаемых представлений.

Если два набора функций преобразуются по НП группы, то их прямое произведение преобразуется, вообще говоря, по приводимому представлению, но его можно легко разложить на неприводимые методом, описанным выше. Приведем некоторые примеры для группы С_3υ:

Заметим, что полносимметричное НП А₁ получается только при перемножении представления самого на себя. Этот результат является общим для точечных групп симметрии.

Рассмотрим интеграл по всему пространству:

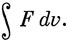
Разложим функцию F по системе функций, преобразующихся по НП группы. Интеграл обращается в нуль, если в этом разложении нет функций, преобразующихся по полносимметричному НП; для всех других функций разложения вклады положительных и отрицательных областей компенсируются при интегрировании по всему пространству.

Теперь рассмотрим два интеграла, которые важны в квантовой механике:

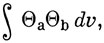
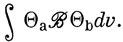
Первый интеграл обращается в нуль, если функции Θ_a и Θ_b не преобразуются по одному и тому же НП группы, поскольку в этом случае прямое произведение представлений не может содержать полносимметричное НП. Аналогично, чтобы второй интеграл не обращался в нуль, необходимо, чтобы прямое произведение представлений, по которым преобразуются функции Θ_a и Θ_b, содержало представление, в котором можно выделить компоненту с теми же свойствами симметрии, что и у оператора Β. Например, если группа симметрии молекулы есть С_3υ, а возмущение обладает симметрией А₂, то это возмущение вызовет взаимодействие двух состояний невозмущенной молекулы в том случае, если одно из них имеет симметрию A₁, а другое - симметрию А₂, или же если оба они обладают симметрией Е.

В последующих главах этой книги теория групп будет использоваться двояким образом. Во-первых, будут применяться обозначения теории групп для характеристики волновых функций там, где это целесообразно для достижения большей ясности. Во-вторых, теория групп позволит упростить вычисления при построении волновых функций и выяснении того, как эти функции изменяются под действием возмущения. Важно понимать, что эти проблемы можно разрешить и без применения теории групп, но в случае высокой симметрии, как, например, у октаэдрических комплексов переходных металлов; математические упрощения, получаемые при помощи теории групп, оказываются довольно значительными.