12.5. Метод ВС и метод атомов в молекуле

Термин "метод ВС" часто употребляется в применении к довольно широкому классу молекулярных расчетов. С одной стороны, к ним относятся строго неэмпирические расчеты, и если при этом используются функции, учитывающие ионную и ковалентную структуры, то такие расчеты соответствуют неэмпирическим расчетам по методу МО с наложением конфигураций. С другой стороны, существует эмпирический подход, основанный на понятии резонанса, который вообще едва ли можно назвать расчетом. Промежуточное положение между этими двумя крайними подходами занимают полуэмпирические расчеты, среди которых наиболее важным является метод атомов в молекулах ^*).

^*) ("Эмпирический" означает, что рассмотрение основано на результатах эксперимента.)

Существенной особенностью метода ВС является то, что волновые функции представляются в виде линейной комбинации функций, соответствующих различным структурным химическим формулам. В эмпирических методах, для того чтобы определить, какие из этих структур вносят наибольший вклад в рассматриваемое состояние молекулы, используют данные химического эксперимента. При этом руководствуются следующими принципами:

1. Ковалентная (двухэлектронная) связь является стабилизующей.

2. Коротким связям соответствуют более низкие энергии, чем длинным.

3. Среди ионных структур наиболее стабильны те, в которых отрицательные заряды находятся у атомов с большей электроотрицательностью, а положительные заряды - у атомов с меньшей электроотрицательностью.

4. Ионные структуры, в которых расстояние между положительными и отрицательными зарядами мало (в силу кулоновского притяжения), имеют более низкую энергию по сравнению с теми, в которых это расстояние велико.

5. Ковалентной гомоядерной структуре А - А почти всегда соответствует более низкая энергия, чем ионной структуре А⁺А^-.

Проиллюстрируем эти положения на примере молекулы воды. На рис. 12.7 приведены структуры, которые следует рассматривать, если предполагать, что кислородная 2s-орбиталь не участвует в образовании связи.

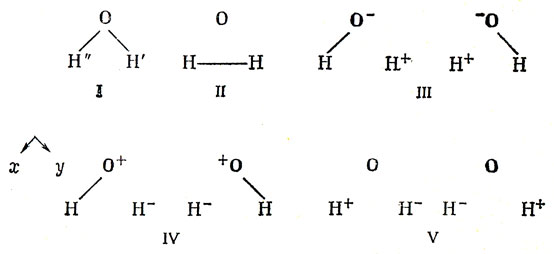
Рис. 12.7. Валентные структуры молекулы Н₂O

В волновой функции основного состояния, очевидно, будет преобладать структура I; она соответствует двух-электронным связям кислородных 2р_х-, 2p_у-орбиталей с водородными 1s-орбиталями. Структуре II будет отвечать более высокая энергия, так как атомы водорода расположены довольно далеко. Маловероятно, чтобы эта энергия была существенно ниже, чем энергия системы изолированных атомов. Ионные структуры III имеют более низкую энергию, чем структуры IV, так как кислород является более электроотрицательным атомом, чем водород; структуры III, вероятно, играют важную роль при построении волновой функции основного состояния. Структуры V характеризуются довольно высокой энергией, потому что для образования ионов Н⁺ и Н^- на расстоянии, соответствующем межъядерному расстоянию молекулы воды, требуется энергия около 4 эв.

Для молекулы воды приводятся только две структуры I и II типа Гайтлера - Лондона, хотя существует три способа группировки четырех орбиталей по парам

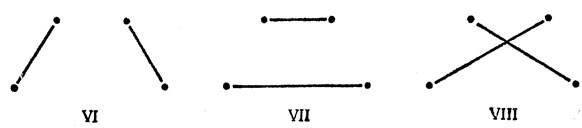
Диаграммы VI и VII соответствуют структурам I и II на рис. 12.7, а диаграмма VIII - двухэлектронной связи между орбиталью 2р_х и 1s-орбиталью атома Н' и такой же связи между орбиталью 2р_у и 1s-орбиталью атома Н". Однако можно показать, что структуры VI, VII и VIII не являются независимыми. Это означает, что волновая функция, написанная для структуры VIII, является линейной комбинацией функций, отнесенных к структурам VI и VII. Иначе говоря, если при построении волновой функции уже учтены структуры VI и VII, то добавление структуры VIII не даст ничего нового.

Существует простое правило, предложенное Румером, для построения независимых структур, в которых 2n орбиталей образуют двухэлектронные связи. Символы орбиталей располагают по кругу (такое расположение не имеет никакого отношения к форме молекулы) и соединяют их попарно линиями. Затем выбирают все те структуры, в которых отсутствуют пересечения этих линий; эти структуры и являются независимыми. Число независимых структур дается формулой

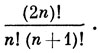
Например, для шести орбиталей найдены следующие пять структур:

которые известны как структуры Кекуле и Дьюара для π-связей бензола (см. гл. 14).

Обратимся теперь к рассмотрению вековых уравнений, которые получаются при использовании набора валентных структур. Во-первых, точное вычисление интегралов с гамильтонианом и интегралов перекрывания в общем случае - сложная задача и в книге этому вопросу отводится лишь очень небольшое место. Недиагональные элементы H_ij и S_ij зачастую имеют тот же порядок величины, что и диагональные. В частности, нередко S_ij бывает больше 1/2. Это, пожалуй, самое неудачное обстоятельство с точки зрения применения метода ВС. Оно означает, что в случае больших молекул надо рассматривать очень много структур (в особенности, если учитывать и ионные структуры); однако многие из них дают, по существу, одно и то же; например, если имеется десять структур и функция одной из них, будучи разложенной по функциям оставшихся девяти, передается на 90%, то можно сказать, что только 10% этой структуры действительно способствует улучшению волновой функции.

Как было показано в гл. 11, при расчете с волновой функцией Гайтлера - Лондона для молекулы Н₂ выражение для энергии содержит два члена - кулоновскую энергию Q и обменную энергию А. Аналогичные члены возникают и в общем интеграле с гамильтонианом при расчете по методу ВС. Существует эмпирический вариант метода ВС, так называемое приближение полного спаривания, в котором полная энергия молекулы выражается через интегралы Q и А сравнительно просто. Считают, что молекулу можно описывать с помощью одной структуры, в которой все АО связаны друг с другом попарно. Кроме того, допускают, что интегралы перекрывания между различными АО равны нулю, а из обменных интегралов учитывают лишь интегралы типа (11.10); интегралы, соответствующие многократному обмену электронов, предполагаются равными нулю. В этих предположениях энергию структуры можно записать в виде

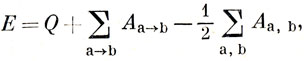
где а → b означает пару орбиталей, образующих связь, и a, b - две орбитали, относящиеся к разным связям.

Хотя приближения, приводящие к выражению (12.31), трудно обосновать, они по крайней мере позволяют получить выражение, на основе которого можно хотя бы качественно представить картину химической связи. Интегралы A_a→b, вносящие наибольший вклад, определяют аддитивность энергии связей, в то время как интегралы A_a,b в основном ответственны за отклонения от этой аддитивности. Рассмотрение этих членов в свое время привело к ряду полезных обсуждений в стереохимии. Однако к настоящему времени в этой области сделано мало. Основное возражение против приближения полного спаривания состоит в том, что весь характер функции Гайтлера - Лондона (см. стр. 248) изменяется, если ее составлять из ортогональных орбиталей; хотя формула (12.31) была выведена в приближении нулевого перекрывания, интегралы A_a→b нельзя вычислять в таком приближении, так как в этом случае не будет получена связь.

Существует еще одно направление в развитии метода ВС, называемое расширенным методом ВС [41], которое приводит к относительно простым формулам для матричных элементов. В этом методе волновые функции строят из гибридных атомных орбиталей так, чтобы интегралы S_a,b были равны нулю при не равных нулю S_a→b. Таким образом, перекрывание имеет место лишь между орбиталями, образующими связь. Однако, хотя эти требования и упрощают задачу, получаемые формулы все же слишком сложны, чтобы рассматривать их здесь.

Метод ВС имеет одно существенное преимущество перед методом МО, которое еще не обсуждалось. Это преимущество заключается в том, что в методе ВС способ построения волновой функции позволяет гораздо легче связать полную энергию молекулы с энергиями отдельных образующих ее атомов. Как уже указывалось, квантовомеханические расчеты довольно точны, если оценивать их по результатам расчетов полной энергии молекулы, но недостаточно удовлетворительны в отношении энергий диссоциации. Например, наилучший расчет по методу ССП для молекулы N₂ дает 99,2% от величины полной энергии, в то время как вычисленная энергия диссоциации равна всего лишь 2,6 эв при экспериментальном значении 9,9 эв.

В 1951 г. Моффит [58] высказал мнение, что причина больших ошибок в вычисленных значениях энергий диссоциации обусловлена тем, что волновые функции, используемые в расчетах, дают также довольно плохое согласие с экспериментом для энергий состояний отдельных атомов. Для иллюстрации этой мысли он в качестве примера приводит молекулу 02. Расчет по методу МО дает для разности энергий возбужденных состояний ³∑_u⁺ и ³∑_u^- величину 10 эв, что плохо согласуется с экспериментальным значением 2 эв. В методе BC ³∑_u⁺ - в основном ковалентная структура, диссоциирующая на нейтральные атомы, в то время как ³∑_u^- - ионная структура O⁺ - О^-. Если выполнить расчеты для отдельных атомов и сравнить суммарную энергию двух ионов O⁺ и О^- с энергией двух нейтральных атомов, то ошибка снова составит около 8 эв.

Моффит заключил тогда, что ошибка в молекулярных расчетах определяется главным образом ошибкой вычисления энергии атомов. Поэтому желательно иметь способ выделения из энергии молекулы той ее части, которая представляет собой энергию отдельных атомов (она может составлять 99% от полной энергии), и затем, вместо того чтобы вычислять значения энергии отдельных атомов, использовать соответствующие экспериментальные величины. Другими словами, надо попытаться вычислять лишь ту часть энергии молекулы, которая действительно является молекулярной. Этот полуэмпирический вариант расчета называется методом атомов в молекулах. Идеи, возникшие первоначально у Моффита, были развиты Хёрли и Араи. Поясним этот метод на примере молекулы LiH.

Построим по методу ВС волновую функцию для молекулы LiH, применяя три функции. Две из них описывают ковалентную связь между 2s-орбиталью лития и водородной 1s-орбиталью и такую же связь между 2pσ-орбиталью лития и водородной 1s-орбиталью, а третья соответствует ионной структуре Li⁺H^-. Используем для этих орбита-лей те же обозначения, что и в выражении (10.34):

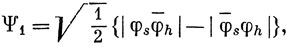
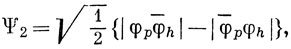
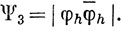
При составлении этих функций предполагается, что два электрона находятся на 1s-AO лития.

Продукты диссоциации, соответствующие этим трем функциям, таковы:

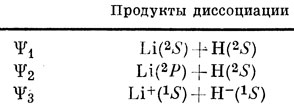
Вычислим теперь энергии продуктов диссоциации W^∼ и сравним эти энергии с определенными из спектроскопических данных (W), а для иона Н^- - с результатами точного расчета. Получим следующие значения (в атомных единицах) [38]:

Отклонения W^∼ от W вызваны тем, что, даже если для АО берутся наилучшие функции, выбранные волновые функции не могут быть точными атомными волновыми функциями, потому что не учитывается полностью электронная корреляция.

Допустим, что на основе наложения функций (12.32) построен вековой определитель

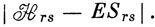
На диагонали этого определителя стоят интегралы, в которые внесем поправки W - W^∼, т. е. вместо H₁₁ поставим H₁₁ + (W₁ - W^∼₁) и т. д. Однако как Уже говорилось, для расчетов по методу ВС характерны большие величины интегралов перекрывания. Если S₁₂ не равно нулю, то это означает, что Ψ₂ содержит некоторый вклад Ψ₁ и, следовательно, H₁₂ содержит долю H₁₁. Поэтому, если вносится поправка в величину H₁₁, надо исправить H₁₂ на величину, пропорциональную S₁₂. Но для того чтобы вековой определитель сохранил симметрию, надо внести в H₁₂ две поправки: W₁ - W^∼₁ и W₂ - W^∼₂. Это приводит к следующему определителю:

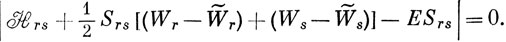
Формула (12.33) учитывает так называемую поправку на внутриатомную корреляцию (ВКП).

В результате неэмпирического расчета по методу ВС для основного состояния молекулы LiH получается следующая волновая функция:

которая дает для энергии диссоциации величину 1,60 эв. Волновая функция с учетом ВКП запишется в виде

а соответствующая энергия диссоциации составит 2,06 эв. Экспериментальное значение энергии диссоцации равно 2,52 эв.

Улучшение, вносимое учетом ВКП в расчеты LiH, менее эффективно, чем в случае тяжелых молекул, как это видно из следующей табл. 12.3. Приведенные в ней результаты Хёрли, основанные на методе ССП, нами несколько улучшены.

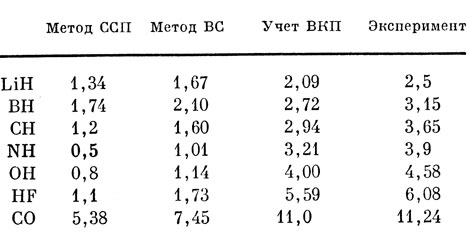
Таблица 12.3 Вычисленные и экспериментальные значения энергии диссоциации (в эв) ^а)

^а) (Данные взяты из работ [37]-[40].)

Учет ВКП увеличивает вклад ионной структуры в волновую функцию основного состояния молекулы LiH, так как для ионной структуры характерна наибольшая корреляционная поправка. Если бы все атомные состояния имели одинаковую энергию корреляции, то не нужна была бы никакая поправка при условии, что энергии диссоциации рассчитываются по отношению к вычисленным же энергиям отдельных атомов. Именно потому, что для различных состояний атома энергии корреляции различны и с изменением межъядерного расстояния изменяется относительный вклад этих состояний в молекулярную волновую функцию, учет ВКП оказывается столь существенным. Вводимые в молекулярную энергию поправки составляются из корреляционных энергий так называемых валентных состояний атомов.

Валентное состояние атома в молекуле определяется той частью молекулярной волновой функции, которая связана с данным атомом, если все атомы развести на бесконечность при сохранении формы молекулярной волновой функции. Проиллюстрируем это, рассматривая валентное состояние кислорода в волновой функции Гайтлера - Лондона для молекулы воды (структура I, рис. 12.7).

Молекулярная функция имеет вид [см. выражение (11.17)]

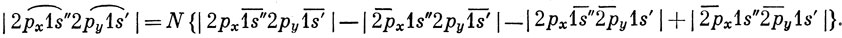
Здесь опущены кислородные 1s-, 2s- и 2р_z-орбитали, занятые каждая двумя электронами. Чтобы получить волновую функцию валентного состояния атома кислорода, надо исключить ту часть волновой функции, которая связана с двумя атомами водорода. Тогда имеем

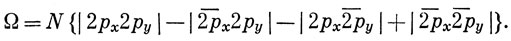
Основному состоянию атома кислорода соответствует конфигурация 1s²2s²2p⁴, при которой возможны термы ³Р, ¹D и ¹S. Первая функция в уравнении (12.35) соответствует спину 1, а потому она относится к терму ³Р. Аналогично последнее слагаемое описывает состояние со спином - 1 и должно относиться также к терму ³Р. Анализируя атомные волновые функции, можно показать, что второе и третье слагаемые в уравнении (12.35) представляют собой смесь функций ¹D- и ³Р-состояний с одинаковым весом. Учитывая вклады всех состояний, т. е. суммируя квадраты коэффициентов каждого из атомных состояний, входящих в определители, получаем, что валентное состояние Ω образуется из ³/₄³P-состояния и ¹/₄¹D-состояния, т. е. не является спектроскопически наблюдаемым состоянием атома кислорода. Отсюда следует, что в функцию Гайтлера - Лондона для молекулы воды следует внести поправку, учитывающую ³/₄ атомной корреляции ³Р-терма и ¹/₄ - ¹D-терма ^*).

^*) (Обзор валентных состояний атомов дан в работе [59].)