12.4. Применение метода МО к многоатомным молекулам

Метод МО применяется к многоатомным молекулам в основном так же, как и к двухатомным. Использование свойств симметрии позволяет сократить вычисления, необходимые для получения набора МО, и это было проиллюстрировано на простом примере молекулы воды в предыдущем разделе.

В разд. 10.5 уже указывалось, что понятие МО не всегда точно определено, но, как будет видно из дальнейших обсуждений, это в некотором отношении расширяет применимость МО.

Пусть имеется набор МО, каждая из которых связана с какой-либо спиновой функцией. Этот набор спин-орбиталей ψ_а, ψ_b, ... можно использовать для построения полной молекулярной функции. Допустим, что в молекуле имеется n электронов. Тогда в качестве первого шага можно было бы взять волновую функцию, в которой этим электронам приписываются n спин-орбиталей с наименьшей энергией; учитывая условие антисимметрии, получим

Теперь, если мы действительно хотим ограничиться волновой функцией такого типа (один слэтеровский определитель, построенный из спин-орбиталей), но все же при этом хотим получить хорошую волновую функцию, то мы должны сделать очень тщательный выбор МО. Их можно было бы получить по методу ССП, описанному в разд. 10.7. Однако это приводит к итеративному расчету, который может оказаться очень громоздким.

Нет необходимости ограничиваться функцией, подобной функции (12.27). Применяя метод конфигурационного взаимодействия, можно взять линейную комбинацию таких слэтеровских определителей с варьируемыми коэффициентами:

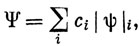
где |ψ|_i означает определитель, построенный из n различных спин-орбиталей. Теперь, если минимизировать с такой функцией энергию (в соответствии с вариационным принципом) относительно коэффициентов c_i, то можно значительно меньше обращать внимания на выбор орбиталей. Если в сумме взять достаточно много слагаемых, то практически несущественно, какие МО при этом используются (если, конечно, они образуют достаточно полную систему); любой недостаток орбиталей можно исправить за счет варьирования коэффициентов с_i. Однако, хотя при этом исчезает необходимость подбирать удачные орбитали, но зато увеличивается работа по определению наилучших коэффициентов c_i. К сожалению, всегда так бывает в квантовой механике - для получения точных волновых функций на каком-либо этапе приходится проводить громоздкие вычисления. Однако в методе МО есть возможность выбора этого этапа: такие вычисления можно делать или при выборе орбиталей, или при учете конфигурационного взаимодействия. Для некоторых задач предпочтительнее первый путь, для других - второй. Обычно наилучший подход заключается в следующем: выбрать орбитали так, чтобы они давали удовлетворительное приближение к самосогласованным орбиталям, и учесть затем взаимодействие по возможности ограниченного числа конфигураций.

Посмотрим, как с помощью наложения конфигураций можно получить достаточно хорошую волновую функцию основного состояния молекулы воды. Беря линейные комбинации кислородных 1s-, 2s- и 2р- и водородных 1s-AO, можно образовать семь независимых МО. Если ограничиться конфигурациями, в которых на низшей по энергии МО (в грубом приближении, это просто кислородная 1s-AO) всегда находятся два электрона, но предположить, что оставшиеся восемь электронов могут быть распределены между остальными шестью МО всеми возможными способами, то всего надо учесть 95 различных электронных конфигураций. Эти конфигурации дают 105 синглетных спиновых состояний, 37 из которых обладают симметрией основного состояния А₁.

Учесть взаимодействие 37 конфигураций - все еще довольно сложная задача, но некоторыми из этих конфигураций, вероятно, можно пренебречь. Например, если основное состояние удовлетворительно описывается функцией типа (12.18), то, пользуясь результатами теории возмущений, мы должны учитывать при наложении конфигураций только те функции, которые дают с функциями основного состояния отличные от нуля интегралы с гамильтонианом. К таким функциям приводят лишь одно- и дважды возбужденные конфигурации, т. е. такие, при которых не более чем два электрона находятся на орбиталях, отличающихся от орбиталей основного состояния (см. стр. 249). Существует только 17 синглетных А₁-функций такого типа для молекулы воды, так что задача становится разрешимой.

Если в качестве исходной взять самосогласованную волновую функцию, которая уже дает достаточно хорошее приближение, то расчет по методу наложения конфигураций еще более упрощается, так как в этом случае равны нулю все интегралы с гамильтонианом, вычисленные с функцией основного состояния и всеми функциями одновозбужденных состояний [см. выражение (10.68)]. В этом случае для молекулы воды остается 14 конфигураций, наложение которых надо учитывать.

Молекула воды - не такая молекула, которую можно было бы назвать большой. И тем не менее видно, что расчет, в котором учитывается взаимодействие конфигураций, оказывается довольно трудоемкой процедурой, даже если включить лишь наиболее существенные конфигурации. Очевидно, что для больших молекул еще невозможно в настоящее время проводить расчеты даже на этом уровне.

Вообще квантовомеханические расчеты в значительной мере согласуются с афоризмом Оккама [73]: "Ничего не следует усложнять без необходимости". В широком понимании это означает, что расчет надо проводить лишь с той степенью точности, которая позволяет ответить на интересующий нас вопрос, и не больше. Например, если нас интересует, почему молекула воды не линейна, то достаточно провести лишь качественные рассуждения или очень простой расчет. Если же нужно выяснить, почему угол между связями в ней равен 105°, а не 90 или 109°, то, как уже указывалось в гл. 5, это требует весьма громоздких вычислений. В общем чем сложнее молекула, тем больше возникает вопросов, относящихся к ней и тем чаще для их решения используются качественные методы. Однако это не означает, что возникающие вопросы не представляют интереса.

Эмпирические направления в методе МО будут детально рассмотрены в последующих главах этой книги. Здесь же только приводится пример использования корреляционных диаграмм, которые оказались очень полезными при обсуждении формы простых многоатомных молекул.

Молекулы Н - А - А - Н могут существовать в четырех геометрически различных формах, в которых атомы водорода занимают эквивалентные положения, как показано на рис. 12.4.

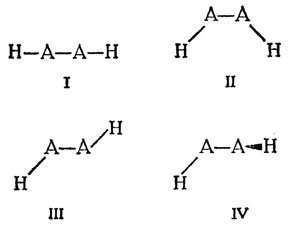
Рис. 12.4. Четыре различные формы молекулы Н - А - А - Н. В структуре IV один из атомов водорода расположен в плоскости рисунка, а другой - в перпендикулярной к ней плоскости

Рассмотрим сначала МО линейной молекулы. Если не учитывать 1s-орбитали атома А, то из 2s- и 2p-орбиталей атома А и 1s-орбиталей атомов водорода можно построить десять МО: две связывающие орбитали связи А - Н (одна имеет симметрию σ_g, а другая - симметрию σ_u), одна связывающая орбиталь (σ_g) связи А - А, две разрыхляющие орбитали (σ_g и σ_u) связи А - Н, одна разрыхляющая орбиталь (σ_u) связи А - А. Далее, две связывающих π_u-орбитали и две разрыхляющих π_g-орбитали соответствуют связи А - А. Порядок возрастания энергии будет, вероятно, следующим:

где звездочкой помечены разрыхляющие орбитали.

Рассмотрим теперь структуру основного и возбужденных состояний молекул С₂Н₂, N₂H₂ и Н₂O₂. В ацетилене, помимо 1s-электронов углерода, имеется десять электронов, которые как раз заполняют все связывающие орбитали. Два электрона в молекуле N₂H₂ и четыре электрона в молекуле H₂O₂ занимают разрыхляющую π_g-орбиталь. Выясним, как изменяются эти орбитали, когда молекулы перестают быть линейными.

Посмотрим, что произойдет, когда один из атомов водорода будет расположен под углом 60° к линии связи А - А в плоскости ху (см. рис. 12.5). При этом изменяется тип гибридизации орбиталей атома A₁ от sp-гибридизации при линейном расположении атомов к sp²-гибридизации. Такое изменение приводит к некоторому увеличению энергии связывающих σ-орбиталей связей А - Н и А - А, так как для обеих связей возрастает р-характер, а р-орбитали имеют более высокую энергию, чем s-орбитали. Однако, по-видимому, это увеличение энергии очень мало. Например, валентное колебание связи С - Н дает в инфракрасной области полосу поглощения с частотой около 3300 см^-1 для ацетилена и около 3000 см^-1 для олефинов. Это соответствует очень малой разнице в энергиях связей С - Н. Наиболее важным результатом этого искажения является снятие вырождения π-орбиталей. Та из двух π-орбиталей, для которой плоскость ху является узловой, не изменяется при искажении. Другая же π-орбиталь с узловой плоскостью xz будет сильно изменяться: ее связывающая компонента π_uy станет менее связывающей, а разрыхляющая компонента π_gy - менее разрыхляющей; так как орбиталь атома А₁, которая в линейной молекуле была просто орбиталью р_у, в изогнутой молекуле участвует в sр²-гибридизации, ее перекрывание с р_у-орбиталью атома А₂ уменьшается. Однако изменение угла между связями увеличивает s-характер этих компонент π-орбиталей, что приводит к понижению энергии. Общий результат оказывается следующим: энергия разрыхляющей π_gy-орбитали понижается при изгибе значительно больше, чем возрастает энергия связывающей π_uy-орбитали.

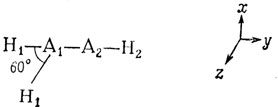
Рис. 12.5. Система координат для изогнутой молекулы Н - А - А - Н

Если и атом Н₂ сместить в плоскости ху, так чтобы образовалась или цис- или транс-конфигурация, то эффект, обусловленный смещением только атома H₁, приблизительно удвоится; если же атом Н₂ сместить в плоскости xz, то наблюдается тот же результат для σ-орбиталей, но теперь изменятся обе компоненты π-орбиталей. На рис. 12.6 качественно представлено изменение энергетических уровней при таких смещениях; изменение разрыхляющих σ-орбиталей не представляет интереса для наших дальнейших обсуждений и поэтому здесь не рассматривается.

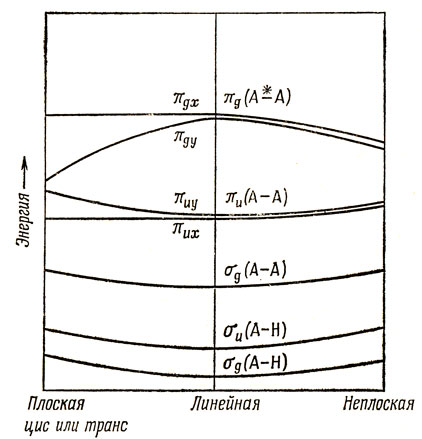
Рис. 12.6. Влияние искажения на энергии молекулярных орбиталей молекулы Н - А - А - Н

Если сделать вполне разумное допущение, что изменения в энергии вызываются главным образом изменениями π-орбиталей, то можно ожидать, что 12-электронная молекула будет обладать плоскими цис- или транс-структурами, причем энергетически более выгодна транс-структура, так как для нее будет меньшим отталкивание несвязанных атомов Н. Молекула N₂H₂ не известна, но у молекулы N₂F₂, для которой также должны быть справедливы приведенные рассуждения, была найдена плоская транс-структура. Молекула Н₂O₂ не является плоской, так как при наличии на разрыхляющей π_g-орбитали четырех электронов более выгодно такое искажение, при котором уменьшается энергия разрыхления для обеих компонент.

Наконец, рассмотрим влияние электронного возбуждения на форму молекулы ацетилена. Первое возбужденное состояние возникает при переходе электрона с π_u-орбитали на π_g-орбиталь. Это должно привести, по-видимому, к изменению формы молекулы (вместо линейной она станет плоской), чтобы скомпенсировать разрыхляющую энергию возбужденного электрона. Полоса поглощения ацетилена лежит в области 2500-2100 А; тонкая колебательная структура которой показывает, что возбужденное состояние имеет плоскую транс-конфигурацию.

В целом ряде работ Уолша [84] показано, что на основе рассмотрения корреляционных диаграмм можно получить полезные качественные выводы относительно формы молекул. Однако интерпретация этих диаграмм требует особого внимания. В тех случаях, когда энергия одних орбиталей возрастает, а других - убывает, не всегда бывает ясно, влияние каких орбиталей преобладает. Кроме того, если из одной конфигурации могут возникать несколько возбужденных состояний, как, например, в случае возбужденной π_u³π_g-конфигурации ацетилена, то не всегда эти состояния будут подвергаться одинаковым изменениям. Для этой конфигурации будут, например, иметь место состояния, коррелирующие с конфигурацией π_uy²π_uxπ_gx плоской изогнутой молекулы, которая, очевидно, нестабильна.