12.3. Роль гибридизации в методах ВС и МО

В гл. 5 было показано, что в теории, основанной на представлении об электронных парах, образующих связь, для объяснения формы молекул, подобных метану, необходимо вводить понятие гибридизации. Волновая функция ВС, отвечающая структуре

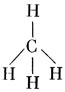
в которой все четыре связи С - Н эквивалентны, должна описывать четыре двухэлектронные связи между четырьмя водородными орбиталями (1s_a, 1s_b, 1s_с, 1s_d) и четырьмя sр³-гибридными углеродными орбиталями (σ_а, σ_b, σ_c, σ_d):

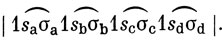
[Использованы обозначения, введенные в выражение (11.19).] Можно было построить волновые функции, в которых 1s-орбитали образуют двухэлектронные связи с 2s- и 2р-АО, но тогда нужно было бы учитывать резонанс между большим числом структур, чтобы получить волновую функцию, соответствующую четырем эквивалентным связям С - Н.

С другой стороны, при рассмотрении молекулы СН₄ по методу МО молекулярные орбитали строят в виде линейной комбинации водородных 1s- и углеродных 2s- и 2р-орбиталей и затем располагают восемь электронов на четырех МО с наиболее низкой энергией. Гибридизация в этом методе не вводится. Поскольку гибридные орбитали есть линейные комбинации АО одного и того же атома, окончательные МО будут одними и теми же независимо от того, образуются ли они в виде линейной комбинации гибридных орбиталей или линейной комбинации атомных орбиталей. Таким образом, гибридизация в методе ВС есть необходимая первая ступень, а в методе МО - не более чем удобный прием.

В методе МО вводится делокализация электронов по всей молекуле, в методе ВС основой является двухэлектронная связь. Рассмотрим молекулу н-гексана с этих двух точек зрения. В этой молекуле имеется четырнадцать связей С - Н, а из химических данных следует, что для разрыва любой из них нужна приблизительно одна и та же энергия (как и в других парафинах). Такое постоянство свойств связи, часто используемое во многих областях химии, следует непосредственно из метода ВС. Связь С - Н в парафинах образуется углеродной sр³-гибридной функцией и водородной 1s-орбиталью, и этим все сказано. С другой стороны, МО в н-гексане не локализованы в области какой-то одной связи С - Н и они не похожи на орбитали метана; поэтому трудно представить себе, как в методе МО может выявиться постоянство свойств связей С - Н.

Если удалить один электрон из н-гексана, то он удалится не из одной определенной связи, а в некоторой степени из всех связей молекулы: каждая из четырнадцати связей С - Н теряет небольшую часть электронного заряда. Это легко объяснить методом МО, так как орбиталь, с которой удален электрон, делокализована по всей молекуле. В методе ВС, с другой стороны, снова приходится вводить понятие резонанса, чтобы теория соответствовала фактам: только для того, чтобы все связи С - Н были эквивалентными, надо учитывать четырнадцать структур с различными одноэлектронными связями С - Н.

Из этих примеров видно, что методы ВС и МО в значительной мере дополняют друг друга, а при определенных предположениях становятся эквивалентными. Действительно, метод ВС, с учетом резонанса структур, может объяснить, почему положительный заряд делокализован по всей молекуле в катионе н-гексана. Теперь нужно выяснить, как свойство аддитивности связей интерпретируется в методе МО. Чтобы это сделать, рассмотрим так называемые эквивалентные орбитали, введенные впервые Леннард-Джонсом, Холлом и Поплом.

Остановимся сначала на некоторых орбиталях, полученных для молекулы воды по методу ССП (см. [23]). Атомные орбитали заданы в системе координат, показанной на рис. 12.2. Молекулярные орбитали должны преобразовываться по неприводимым представлениям группы симметрии молекулы воды С_2υ. Кислородные АО (1s, 2s, 2р_х, 2р_у, 2p_z) уже удовлетворяют этому требованию. Если водородные 1s-орбитали взять в виде линейных комбинаций h₁ и h₂ (см. стр. 143, где такая операция выполнена для молекулы формальдегида), то все АО можно будет классифицировать по неприводимым представлениям группы C_2υ (см. табл. 8.5). Функции, преобразующиеся по представлению A₁, симметричны относительно всех операций группы, а преобразующиеся по представлениям В₂ и B₁ - антисимметричны относительно поворота вокруг оси z[C₂(z)] и отражений в плоскостях σ_υ (плоскость xz) и σ'_υ (плоскость yz) соответственно. Среди перечисленных выше АО нет преобразующихся по представлению А₂, т. е. антисимметричных относительно отражений в плоскостях σ_υ(xz) и σ'_υ (yz).

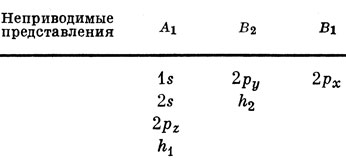
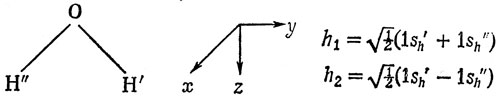
Pис. 12.2. Оси координат для молекулы Н₂O и симметризованные комбинации водородных орбиталей

Для построения МО можно комбинировать только АО, обладающие одинаковыми свойствами симметрии. Это означает, в частности, что 2р_х-орбиталь - несвязывающая. В табл. 12.2 приведены пять низших по энергии самосогласованных МО, полученных Эллисоном и Шуллом при угле 105° между связями.

Таблица 12.2. Самосогласованные орбитали для молекулы воды [24]

Низшая по энергии орбиталь ψ₁ почти целиком состоит из 1s-АО, а в ψ₂ основной вклад вносит 2s-AO, так что эта орбиталь в значительной степени тоже несвязывающая. Молекулярные орбитали ψ₃ и ψ₄ - преимущественно связывающие орбитали. В основном состоянии десять электронов занимают пять низших по энергии орбиталей, так что соответствующую волновую функцию, построенную по методу МО, можно записать в виде

Если строки (или столбцы) определителя складывать между собой или вычитать друг из друга, то величина определителя не изменится. Например, функция (12.18) идентична функции

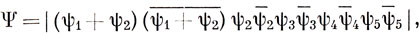
которая выводится из равенства (12.18) добавлением к первому столбцу третьего и ко второму - четвертого. Теперь можно сказать, что электроны занимают орбитали ψ₁ + ψ₂, ψ₂, ψ₃, ψ₄, ψ₅, и, конечно, можно получить еще много других наборов из пяти орбиталей, как ортонормированных, так и не удовлетворяющих условию ортонормировки. Существует один набор орбиталей, которому отвечает идея МО, локализованных на связях; эти орбитали называются эквивалентными.

МО преобразуются по НП группы симметрии. В случае группы C_2υ, не содержащей многомерных НП, любая операция симметрии либо изменяет знак МО, либо сохраняет ее неизменным. Допустим, однако, что нужно получить орбитали, локализованные на связях О - Н в молекуле воды. Должны быть две такие орбитали, которые не преобразуются ни по одному из НП группы, но переходят одна в другую при операциях симметрии. Это показано на рис. 12.3. МО ψ₃ и ψ₄ являются основными связывающими орбиталями (табл. 12.2); ψ_b1 и ψ_b2 - орбитали, соответствующие локализованной связи, определенные таким образом, что они взаимно ортогональны и при операциях поворота С₂ и отражения σ (xz) в плоскости xz переходят одна в другую. МО ψ_b1 и ψ_b2 можно записать в виде ортогональных линейных комбинаций МО ψ₃ и ψ₄:

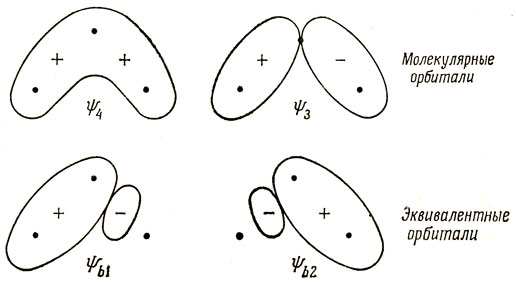
Рис. 12.3. Эквивалентные молекулярные орбитали для молекулы Н₂O

Можно также преобразовать несвязывающие орбитали ψ₂ и ψ₅ в несвязывающие эквивалентные орбитали ψ_l1 и ψ_l2, расположенные под углом к плоскости молекулы воды, так что четыре орбитали ψ_b1, ψ_b2, ψ_l1 и ψ_l2 направлены к вершинам тетраэдра, так как МО ψ₂ и ψ₅ не являются строго (определенно) несвязывающими; эквивалентные орбитали в действительности представляют собой смесь всех МО ψ₂, ψ₃, ψ₄, ψ₅. Эллисон и Шулл получили следующие волновые функции:

Волновая функция

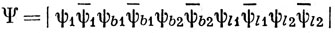
идентична функции (12.18), хотя они и кажутся различными.

Всегда можно взять такую смесь 2р_у- и 2р_z-функций, которая дает 2р-орбиталь, ориентированную вдоль некоторого направления в плоскости yz. Например,

где 2р_φ - р-орбиталь, составляющая с осью z угол φ = 34°. Помня об этом и рассматривая равенства (12.21), легко увидеть что эквивалентные связывающие орбитали построены главным образом из водородной 1s-орбитали и 2p_φ-орбитали, ориентированной, хотя и не точно, вдоль связи.

Можно сказать, что гибридные АО эквивалентны орбиталям атома. Например, предположим, что рассматривается атом углерода в 2s2p³-конфигурации с одинаковой ориентацией спинов всех электронов. Это состояние является одним из пяти возможных для терма ⁵S и имеет волновую функцию

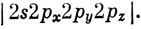
Идентичная ей функция есть

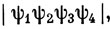
где эти ψ - четыре sp³-гибрида, определенные из равенств (5.3) и (5.4). Эти образующие тетраэдр гибриды представляют собой эквивалентные орбитали атома углерода в потенциальном поле тетраэдрической симметрии (например, в таком, как поле, создаваемое четырьмя атомами водорода в метане). Если в качестве первого шага в методе МО учитывается возможность гибридизации и МО берутся затем в виде линейных комбинаций орбиталей (атомных или гибридных), сильно перекрывающихся между собой, то в результате получаются МО, соответствующие локализованным связям и дающие обычно хорошее приближение к эквивалентным орбиталям в молекуле. В качестве примера возьмем молекулу метана. Если тетраэдрический гибрид σ₁ комбинировать с орбиталью 1s₁ атома водорода, к которому направлена орбиталь σ₁, и построить соответствующую этой связи МО

то функция ψ₁ дает хорошее приближение к эквивалентной орбитали метана (точная эквивалентная орбиталь отличается от ψ₁ только тем, что содержит незначительную примесь функций 1s₂, 1s₃ и 1s₄).

Подытожим теперь сказанное. МО преобразуются по одному из представлений группы симметрии. Волновая функция, записанная в виде слэтеровского определителя, составленного из этих МО, передает делокализацию электронов и наиболее пригодна, например, для описания ионизации молекулы. Поскольку волновая функция представлена в виде определителя (чтобы удовлетворить принципу запрета Паули), МО можно преобразовать в другие наборы орбиталей, которые дают ту же самую волновую функцию. Функции одного из этих наборов называют эквивалентными. При операциях группы симметрии каждая эквивалентная орбиталь переходит в одну из остальных. Эти функции соответствуют достаточно хорошей локализации электронов в связях или же представляют собой орбитали неподеленных пар электронов. Они образуют наилучший из возможных в методе МО базис для описания аддитивных по связям свойств молекулы. Если в методе ВС молекулу можно удовлетворительно описывать посредством локализованных в связях электронных пар, то, как оказывается, эквивалентные орбитали позволяют сделать то же самое. Для молекул типа бензола, где при описании по методу ВС π-связи не локализованы, также невозможно получить и локализованные эквивалентные орбитали. В этом отношении оба метода согласуются.