Главa 13. Теория поля лигандов

13.1. Простая теория кристаллического поля

Ионы переходных металлов представляют интерес для химии главным образом потому, что они могут образовывать комплексы. В большинстве комплексов катион переходного металла окружен шестью молекулами или анионами (их называют лигандами), расположенными в вершинах более или менее правильного октаэдра. Такое строение имеют большинство комплексов даже в тех случаях, когда на первый взгляд оно кажется невозможным. Например, кристаллы CuSO₄·5H₂O и FeCl₃ оба содержат октаэдрически окруженные катионы, как показано на рис. 13.1. Ионы переходных элементов первого ряда (от Ti до Сu), имеющие от четырех до семи d-электронов, образуют комплексы двух типов: число неспаренных электронов в комплексах одного типа больше, чем в комплексах другого. Это полностью подтверждается электронными спектрами таких комплексов. Например, двухвалентное железо (3d⁶) образует и "зеленый" [Fe(H₂O)₆]²⁺ и "желтый" [Fe(CN)₆]^4- комплексы. Первый из них содержит у каждого атома железа четыре неспаренных электрона и парамагнитен; второй вовсе не содержит неспаренных электронов и, следовательно, диамагнитен.

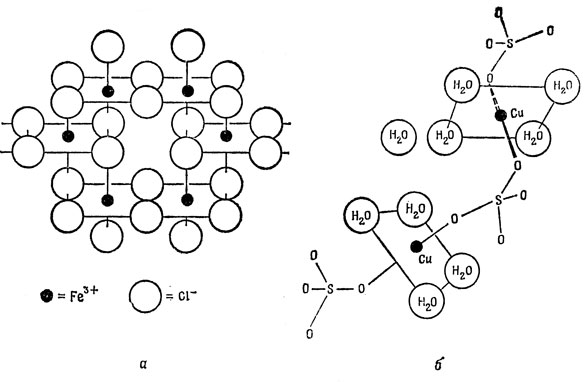
Рис. 13.1. Октаэдрическое расположение в FeCl₃ и CuSO₄·5H₂O

Для объяснения различий между двумя типами комплексов были предложены три теории; в каждой из них решающее значение имеет заполнение d-орбиталей катиона. Первой теорией, получившей общее признание, была теория Полинга, разработанная на основе метода ВС. Согласно Полингу, ионы, участвующие в образовании октаэдрического комплекса, находятся в состоянии или d²sp³ (т. е. 3d²4s4p³)-, или sp³d² (т. е. 4s4р³4d²)-гибридизации, и эти орбитали образуют связи с лигандами. В первом случае три 3d-орбитали, а во втором случае все пять 3d-орбиталей остаются неиспользованными.

Поэтому максимально возможное число неспаренных d-электронов в первом случае равно трем, а во втором - пяти; этим и обусловлено возникновение комплексов двух типов. В настоящее время эта теория почти полностью утратила свое значение, хотя иногда и употребляется принятая в ней номенклатура, например, названия "внутренние" (с 3d-орбиталями, участвующими в гибридизации) и "внешние" (с 4d-орбиталями) комплексы. Наиболее серьезным недостатком этой теории является то, что в ней совершенно не рассматриваются разрыхляющие орбитали и, следовательно, она неспособна объяснить электронные спектры, а также существование довольно стабильных комплексов с внутренними орбиталями, содержащих более шести d-электронов. Хотя теория Полинга и внесла существенный вклад в химию комплексов металлов, тем не менее в дальнейшем она не рассматривается ^*).

^*) (Более подробное описание этой теории дано в книге [66].)

Более удовлетворительными оказались две другие теории - кристаллического поля и поля лигандов. Первая создана Ван Флеком и является полностью электростатической теорией, вторая же представляет объединение электростатической теории и метода МО. Расчеты в обеих теориях имеют много общего, поэтому, прежде чем вводить в рассмотрение МО, обсудим более подробно теорию кристаллического поля.

В теории кристаллического поля считают основной причиной стабильности комплекса электростатическое притяжение, возникающее между ионным или полярным лигандом (например, Сl^-, Н₂O) и центральным катионом. Рассматриваемые силы взаимодействия сходны с теми, которые имеют место в ионных кристаллах; отсюда и происходит название теории. Существенным шагом теории кристаллического поля является установление того факта, что хотя в изолированном катионе все пять d-орбиталей вырождены, под влиянием октаэдрического кристаллического поля это вырождение снимается.

При описании октаэдрического комплекса обычно принято оси декартовых координат совмещать с осями симметрии четвертого порядка октаэдра. Из этого следует, что р-орбитали катиона остаются вырожденными в комплексе, так как они находятся в эквивалентных положениях по отношению к лигандам. Однако это не имеет места для d-орбиталей. В самом деле, две из них, d_x²-y² и d_z², ориентированы вдоль осей координат, в то время как остальные три, d_xy, d_yz и d_zx, ориентированы вдоль линий, не совпадающих с осями координат. В соответствии с этим энергии этих двух групп d-орбиталей различны ^*). Если предполагать, что поле лигандов приближенно совпадает с полем точечных отрицательных зарядов, то ясно, что электрон, находящийся на d_xy-, d_yz- или d_xz-орбитали, имеет более низкую энергию, чем электрон на d_z²- или d_x²-y²-орбитали. Это показано на рис. 13.2. Та часть потенциала, которая действует равным образом на состояния обеих групп, несущественна для проводимого обсуждения и не учтена на рис. 13.2.

^*) (На стр. 44 мы отмечали, что орбитали d_z² и d_x²-y² в действительности эквивалентны, хотя они и кажутся различными.)

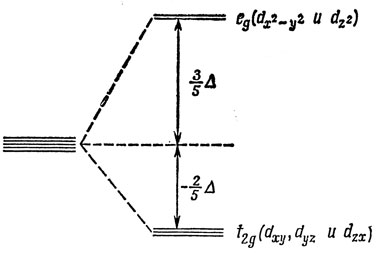
Рис. 13.2. Расщепление d-уровней в октаэдрическом кристаллическом поле

На рис. 13.2 две упомянутые выше группы d-орбиталей обозначены в соответствии с НП группы октаэдра O_h, по которым они преобразуются (групповые символы представлений принято записывать строчными буквами для обозначения орбиталей и прописными для обозначения состояний). Иногда обозначение e_g заменяется на d_γ или γ₃, a t_2g - на d_ε или γ₅.

Расстояние между расщепленными уровнями t_2g и e_g обозначают символом Δ (или 10Dq) ^*). Δ изменяется при переходе от одного комплекса к другому, но для любого иона-комплексообразователя можно расположить лиганды в порядке производимого ими расщепления Δ. Было найдено, что этот порядок почти не зависит от природы центрального иона. Поскольку величину расщепления Δ обычно определяют из спектроскопических данных, такой ряд называют спектрохимическим рядом. Величина Δ возрастает в следующей последовательности:

^*) (Если потенциал разложен в ряд по сферическим гармоникам (3.6), то первый член, приводящий к снятию вырождения d-орбиталей, соответствует l = 4. Выражая его в декартовых координатах, получаем

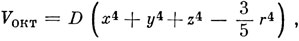
где D = 35e²Z/4a⁵ в предположении, что лиганды представляют собой точечные заряды, расположенные на расстоянии а от катиона. Расщепление между уровнями равно в этом случае 5e²Z‾r⁴/3a⁵, где r‾ - среднее расстояние d-электрона от ядра катиона. Обычно вместо 5e²Z‾r⁴/3a⁵ пишут 10Dq, где

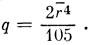
Тогда 10Dq - теоретически определяемая величина. Мы предпочитаем обозначение Δ и рассматриваем эту величину как чисто эмпирическую.)

Для двухвалентных ионов переходных металлов первого ряда Δ имеет величину порядка 12000 см^-1, а для трехвалентных - порядка 20000 см^-1. Для ионов переходных металлов второго и третьего рядов Δ характеризуется значительно большей величиной.

Рис. 13.2 дает простое объяснение магнитных свойств комплексов, о которых упоминалось в начале этой главы, без внесения принципиальных изменений в описание связи по методу ВС. В табл. 13.1 приведены электронные конфигурации двухзарядных и трехзарядных положительных ионов элементов от титана до меди. Нужно разместить от одного до девяти электронов на e_g- и t_2g-орбиталях. При этом необходимо учитывать два способа получения наиболее низкой энергии: либо расположить электроны по возможности на различных пространственных орбиталях (при этом обменная энергия максимальна, а энергия кулоновского отталкивания минимальна), либо заполнить прежде всего низшие по энергии орбитали. Можно различать два предельных случая: когда Δ мало ("высокоспиновые" комплексы или комплексы слабых полей) и когда Δ велико ("низкоспиновые" комплексы или комплексы сильных полей). В комплексах слабых полей заполнение электронами орбиталей e_g и t_2g происходит последовательно, в соответствии с рис. 13.3; в этом случае Δ достаточно мало для того, чтобы можно было применять правило Гунда. Поэтому спиновая мультиплетность такая же, как и для свободного иона, достигающая максимума в конфигурации d⁵.

Таблица 13.1. Число 3d-электронов для двухзарядных и трехзарядных катионов элементов от титана до меди, ни один из этих ионов не содержит 4s- или 4p-электронов

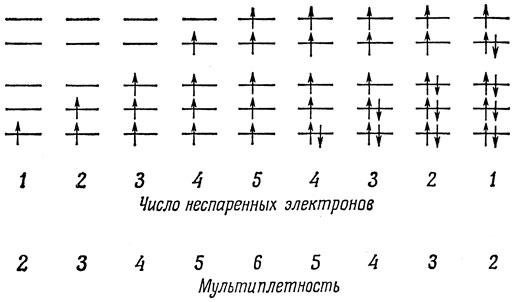
Рис. 13.3. Распределение электронов в комплексах слабых полей (высокоспиновых)

Когда Δ велико, преобладает энергия кристаллического поля, и возникают электронные конфигурации, показанные на рис. 13.4.

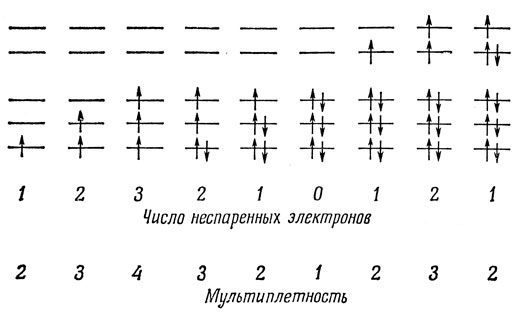
Рис. 13.4. Распределение электронов в комплексах сильных полей (низкоспиновых)

В теории кристаллического поля магнитные свойства комплексов определяются балансом между энергией взаимодействия электронов и энергией кристаллического поля. Позднее, при рассмотрении теории поля лигандов можно увидеть, что еще один фактор играет существенную роль - протяженность π- и π-связей. После всего сказанного становятся ясными термины, употребляемые для обозначения двух типов комплексов. "Высокоспиновый" и "низкоспиновый" - феноменологические понятия, а "слабое поле" и "сильное поле" характеризуют величину кристаллического поля.

Теория кристаллического поля дает довольно простое объяснение закономерностей, которым подчиняются теплоты образования ряда комплексов, соответствующих различным центральным катионам. Поскольку энергия электрона, находящегося на t_2g-орбитали, на 2/5 Δ ниже принятой за начало отсчета средней энергии всех d-орбиталей в кристаллическом поле, а энергия электрона, находящегося на e_g-орбитали, выше этой средней энергии на 3/5 Δ, можно вычислить общее понижение энергии в кристаллическом поле для любой электронной конфигурации. Результаты такого расчета для комплексов слабых полей приведены в табл. 13.2. Аналогичную таблицу можно было бы составить и для комплексов сильных полей.

Таблица 13.2. Энергии стабилизации кристаллическим полем для октаэдрических комплексов слабых полей

В качестве примера рассмотрим теплоты гидратации двухвалентных ионов переходных элементов первого ряда. Экспериментальные значения ложатся на кривую, имеющую излом в точке, соответствующей иону Мn²⁺. Если вычесть из теплоты гидратации вычисленную для каждого иона описанным выше способом энергию стабилизации кристаллическим полем (значение Δ определяется на основе электронных спектров гидратов), то получающиеся энергии ложатся почти на прямую линию. Это показано на рис. 13.5 ^*).

^*) (Более подробное обсуждение и другие примеры, относящиеся к этому вопросу, можно найти в работе [30].)

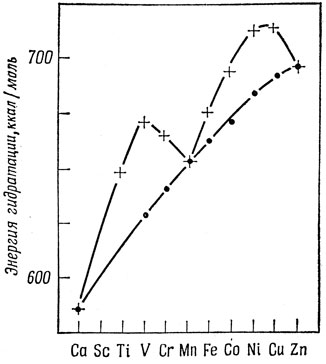
Рис. 13.5. Экспериментальные и исправленные теплоты гидратации двухвалентных ионов переходных элементов первого ряда. + экспериментальные данные; ● экспериментальные данные с учетом поправки на энергию стабилизации кристаллическим полем