
13.2. Детальное рассмотрение комплексов слабых полей в теории кристаллического поля
Рассмотрим теперь более подробно влияние кристаллического поля на d-орбитали. В теории кристаллического поля пренебрегают любым перекрыванием между орбиталями катиона и лигандов и рассматривают только действие электростатического возмущения на орбитали катиона.
При расчете уровней энергии изолированного атома или иона по схеме Рассела - Саундерса (стр. 157) прежде всего учитывают кулоновское притяжение между всеми электронами и ядром, затем межэлектронное отталкивание и, наконец, спин-орбитальное взаимодействие, в соответствии с уменьшением роли различных взаимодействий (рис. 9.2). В теории кристаллического поля поступают точно так же, учитывая, кроме того, на соответствующем этапе возмущающее действие кристаллического поля. При этом для ионов переходных металлов первого ряда кристаллическое поле вводится либо перед учетом межэлектронного отталкивания (в комплексах сильных полей), либо после него перед учетом спин-орбитального взаимодействия (в комплексах слабых полей). На практике оказывается, что для переходных элементов первого ряда даже самые слабые кристаллические поля вносят больший вклад, чем спин-орбитальное взаимодействие, хотя это не всегда верно для переходных элементов второго и третьего рядов и совсем не наблюдается для редкоземельных элементов. Термы, возникающие из конфигурации (d)n в схеме Рассела - Саундерса, можно найти, пользуясь методами, описанными в гл. 9. Термы, соответствующие основному состоянию, определяются по правилу Гунда и приведены в табл. 13.3.
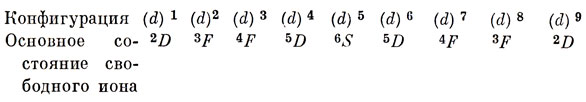
Таблица 13.3. Основные термы конфигураций (d)1 → (d)9
Рассмотрим теперь влияние слабого поля на эти основные состояния. Поскольку электростатическое поле не взаимодействует непосредственно со спином электрона, необходимо лишь установить, как кристаллическое поле устраняет орбитальное вырождение. Если не считать конфигурацию (d)5, то в табл. 13.3 встречаются лишь D- и F-термы, и вполне достаточно обсудить конфигурации (d)1 и (d)2. Тогда остальные конфигурации, за исключением (d)5, можно будет рассмотреть аналогичным образом.
Термы D вырождены пятикратно, а термы F - семикратно. Однако из теории групп следует, что в случае октаэдрической симметрии орбитальное вырождение не может быть более чем трехкратным (это видно из таблицы характеров группы Oh; см. табл. 13.4), и поэтому в октаэдрическом комплексе D- и F-термы должны расщепиться по крайней мере на две и три компоненты соответственно. Пользуясь теорией групп, выясним сначала, как расщепляется D-терм.
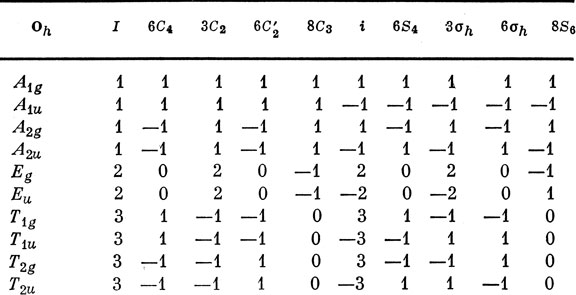
Таблица 13.4. Таблица характеров группы Oh
Очевидно, что пять компонент D-терма обладают теми же свойствами симметрии, что и пять d-орбиталей, так как символы d и D означают, что угловая зависимость соответствующих функций описывается сферическими гармониками с l = 2. При любой операции группы симметрии каждая из компонент преобразуется в линейную комбинацию всех пяти. Таким образом, эти пять компонент образуют базис представления группы, и нас интересует разложение этого представления на неприводимые.
Характер представления - это сумма диагональных элементов матриц, соответствующих операциям группы. В характер вносят вклад только те компоненты, которые остаются неизменными при операции симметрии. Для начала возьмем две наиболее простые операции: тождественное преобразование I сохраняет неизменными все пять компонент, следовательно, χ (I) = 5; при операции инверсии знак всех компонент не меняется (так как d-орбитали относятся к g-состояниям), поэтому χ (i) = 5. Для других операций определить характеры труднее, но это можно сделать, рассматривая изменение волновых функций при повороте на угол φ.
Допустим, что нас интересует результат действия поворота вокруг выделенной оси в пространстве. Существует множество способов выбора волновых функций, соответствующих компонентам D-терма (d-орбиталям), потому что все пять компонент вырождены. Ясно, что мы будем стремиться выбрать такие волновые функции, которые делают рассмотрение настолько простым, насколько это возможно. Этого можно добиться, совместив ось вращения с осью z и беря волновые функции в комплексной форме (3.9). Тогда операция вращения меняет лишь начало отсчета переменной φ, от которой пять компонент зависят следующим образом [см. выражения (3.9)]:
e2iφ, eiφ, 1, е-iφ, е-2φ.
При повороте на угол α эти функции переходят в
e2i(φ+α), ei(φ+α), 1, e-i(φ+α), e-2i(φ+α),
т. е. можно написать, например, что
Rα e2iφ = е2iα · e2iφ, (13.1)
или, записывая действия оператора Rα на все пять компонент в матричном виде, имеем

Характер матрицы, представляющей операцию Rα над компонентами D-терма, равен
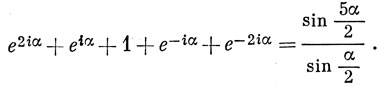
*) (Этот результат получается суммированием левой части по правилам геометрической прогрессии.)
Этот результат можно обобщить на случай произвольного состояния со значением орбитального момента, равным L; ему соответствуют 2L + 1 компонента, зависимость которых от φ передается функциями eiLφ, еi(L-1)φ + ... + e-iLφ. Интересующий нас характер равен
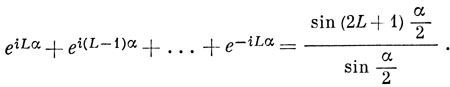
Вернемся снова к группе Oh. Чтобы найти характер, соответствующий операции С4 при действии ее на компоненты D-терма, ось z направим по оси четвертого порядка, тогда из формулы (13.3) при α = 90° получим, что χ (С4) = sin 225° / sin 45° = - 1. Аналогично для операций С2 и С'2 (α = 180°) находим характеры, равные 1, и, наконец, для операции С3 (α = 120°, ось z направлена по оси С3)
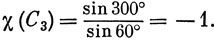
Вычисленные характеры позволяют установить, что приводимое представление, базисом которого являются пять компонент D-терма, разлагается на неприводимые Е + Т2, но не определяют, какой из значков g или u следует им приписать. Поскольку интересующие нас D-состояния получаются из конфигурации (d)n, a d-орбитали симметричны относительно инверсии в центре симметрии, то разложение по НП имеет вид Eg + Т2g. Для D-состояния, возникающего из конфигурации (р)2, в октаэдрическом поле лигандов также обнаруживаются компоненты Eg и T2g, а для образованного из конфигурации pd в таком же поле - Еu и Т2u.
Следуя тому же способу, получаем (см. задачу 13.2), что F-термы расщепляются в октаэдрическом поле на компоненты Т1g + T2g + A2g. Теперь нужно определить относительные энергии компонент D- и F-термов. Начнем с рассмотрения случая (d)1. Еще раньше был выяснен характер расщепления орбиталей и полученные результаты сведены в табл. 13.5.

Таблица 13.5. Волновые функции и энергии состояний, возникающих из конфигурации (d)1 в октаэдрическом поле
Если электрон занимает t2g-орбиталь, возникает состояние с симметрией 2T2g; если занята eg-орбиталь, то состояние обладает симметрией 2Eg. Волновые функции в комплексной форме запишем следующим образом: (l, ml) = (2, 2), (2, 1), (2, 0), (2, -1), (2, -2); соответствующие действительные функции приведены в табл. 13.5.
Возмущение уровней энергии этих орбиталей, создаваемое кристаллическим полем, дается следующими выражениями [в выражении (6.50) нужно вместо H' подставить Vокт]:
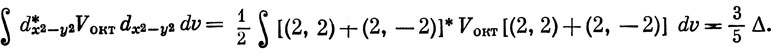
Аналогично
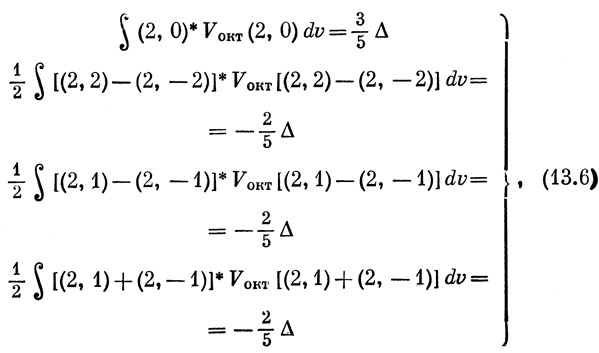
где, например,
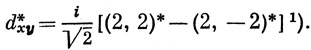
*)
Поскольку теперь оперируем с комплексными функциями, всегда следует помнить, что в любом интеграле типа ∫ ψ*Bψ dυ стоящая слева функция должна быть комплексно сопряженной.
Все эти интегралы можно записать в виде суммы интегралов (естественно, кроме второго). Например, для интеграла (13.5) имеем
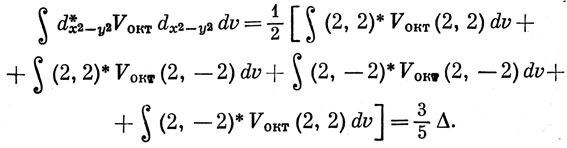
Используя равенство (2, -2)* = (2, 2) (см. разд. 3.9) или ∫ d*x2-y2 Vокт dxy dυ = 0, получаем
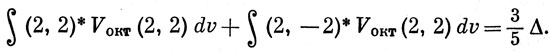
Теперь можно вычислить поправки к энергии комплексных d-орбиталей, обусловленные возмущающим действием октаэдрического поля. Комбинируя выражения (13.5) и (13.6), находим
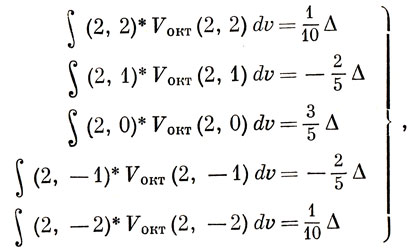
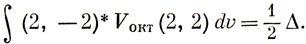
Особо отметим интеграл (13.8); это единственный интеграл с различными d-орбиталями, отличный от нуля. Всю совокупность интегралов взаимодействия удобно записать в виде таблицы (матрицы) *)

*) (Мы называем интегралы вида (13.7) интегралами взаимодействия по вполне понятным причинам. В литературе пользуются названием "матричный элемент", и применительно к интегралам типа (13.8) - "недиагональный матричный элемент".)
Таким образом, мы выразили величину расщепления через интегралы, содержащие не действительные, а комплексные функции. Это не дает никаких упрощений в простом случае конфигурации (d)1 [в силу наличия интеграла взаимодействия между функциями (2, 2) и (2, -2)]. Однако в случае конфигурации (d)2 можно с их помощью получить значения энергии.
Волновые функции 3F-терма, возникающего из конфигурации (d)2, легко получаются с помощью оператора сдвига, рассмотренного в гл. 9. Расчеты в теории кристаллического поля с использованием этих функций хотя и совсем просты, но очень длинны, и потому охарактеризуем их лишь в общих чертах. Функции двух электронов терма 3F обозначим (3,3), (3, 2), (3, 1), (3, 0), (3, -1), (3, -2), (3, -3), в согласии с номенклатурой для (d)1.
Кристаллическое поле не действует на спин, и поэтому достаточно рассмотреть состояние с каким-нибудь одним значением проекции спина (например, Ms = 1).
Рассмотрим один пример для иллюстрации того, как вычисляются интегралы взаимодействия с функциями двух электронов. Функция (3, 3) может возникнуть только в том случае, если один электрон находится на d-орбитали (2, 2), а другой - на d-орбитали (2, 1). Запишем эту функцию в виде определителя
(3,3) = |(2, 2) (2, 1)| = √1/2 [(2, 2)1 (2, 1)2 - (2, 2)2 (2, 1)1], (13.10)
где оба электрона имеют спин α и обозначены цифрами 1 и 2. Тогда
∫ (3, 3)* Voкт (3, 3) dυ = 1/2 ∫∫ [(2, 2)1 (2, 1)2 - (2, 2)2 (2, 1)1]* Voкт [(2, 2)1 (2, 1)2 - (2, 2)2 (2, 1)1] dυ1 dυ2 (13.11)
Но так как Vокт действует на координаты каждого из электронов независимо, т. е. Vокт = Vокт(1) + Vокт(2), интеграл (13.11) равен
∫ (2, 1)2* Vокт (2) (2, 1)2 dυ2 + ∫ (2, 2)1* Vокт (1) (2, 2)1 dυ1. (13.12)
Значения этих двух интегралов определяются из выражений (13.7), тогда
∫ (3, 3)* Vокт (3, 3) dυ = - 2/5 Δ + 1/10 Δ = - 3/10 Δ. (13.13)
Продолжая таким же образом, можно вычислить все энергии возмущения. Результаты расчетов представлены в виде матрицы возмущения (13.14):
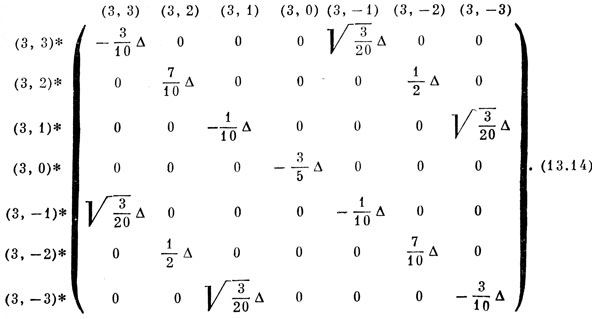
Как и в случае (d)1, функции с четырьмя различными МL перемешиваются, и обусловленное кристаллическим полем взаимодействие между функциями (3, 3), (3, -1) такое же, как и между функциями (3, -3), (3, 1).
Чтобы получить собственные функции и собственные значения, необходимо решить систему уравнений (6.67):
∑i ci (Hik - ESik) = 0, где H = Vокт.
Если матрицу расположить в виде (13.15), то становится очевидным, что необходимо решать вековые уравнения только второй степени:
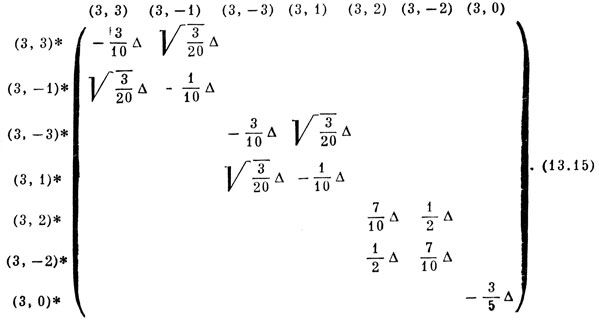
Решая обычным путем эти уравнения, получим собственные функции и собственные значения, которые приведены в табл. 13.6.

Таблица 13.6. Компоненты терма 3F (d2) в поле симметрии Oh a)
а) (Мы построили волновые функции для случая, когда оба электрона имеют спин α. Они представляют собой лишь одну компоненту для каждого триплетного состояния. Спиновая мультиплетность отмечена вверху слева около символа, обозначающего симметрию.)
Удобно представить данные табл. 13.5 и 13.6 графически. Это сделано на рис. 13.6.
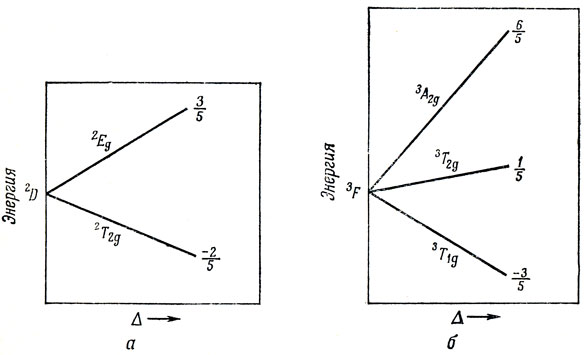
Рис. 13.6. Расщепление D- и F-термов в октаэдрическом кристаллическом поле. Значения тангенса угла наклона указаны на соответствующих прямых
Рис. 13.6 можно легко изменить, если требуется включить другие конфигурации, приводящие к D- или F-термам. Рассмотрим, например, основной терм 4F, возникающий из конфигурации (d)3. Конфигурация (d)3 отличается от сферически симметричной конфигурации (d)5 наличием двух "дырок". Расщепление терма 4F (d3) будет в точности таким же, как и терма 3F (d2), с той только разницей, что Vокт, который соответствовал отталкиванию электронов, теперь будет отвечать притяжению дырок. Поэтому для получения диаграммы расщепления терма 4F (d3), график на рис. 13.6,б нужно обратить. Из аналогичных рассуждений следует, что график на рис. 13.6,б действителен для терма 4F (d7), но должен быть обращен для терма 3F (d8). Подобно этому график на рис. 13.6,а соответствует терму 5D (d6), но должен быть обращен для термов 5D (d4) и 2D (d9).
Остается только обсудить основной терм 6S, возникающий из конфигурации (d)5. Поскольку в этом случае орбитального вырождения нет, отсутствует и расщепление кристаллическим полем.
Из рассмотрения терма 3F (d2) в слабом поле вытекает одно интересное следствие. Энергия основного состояния на 3/5 Δ ниже нулевой энергии. Какое заполнение t2g- и eg-орбиталей приводит к такому понижению энергии? Из рис. 13.2 видно, что заселенности должны быть 9/5 для орбитали t2g и 1/5 - для орбитали
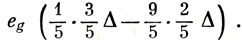
Под действием слабого поля на конфигурацию (d)2 небольшая часть электронной плотности выталкивается на нестабильную орбиталь eg. Отсюда следует, что в предыдущем обсуждении магнитных свойств комплексов ионов мы были не совсем правы, помещая в случае конфигурации (d)2 в слабом поле оба электрона на орбитали t2g. Однако эту малую поправку, полученную здесь, едва ли можно обнаружить на опыте.
Нецелочисленное заполнение t2g- и eg-орбиталей получается также в слабом кристаллическом поле для терма d7 (4F) в октаэдрическом и термов d3 (4F) и d8 (3F) в тетраэдрическом комплексах.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'