13.3. Комплексы сильных полей

Перейдем теперь к обсуждению комплексов сильных полей. Для этого необходимо рассмотреть все термы каждой конфигурации, а не только основной, так как в силу большой величины Δ основное состояние комплекса возникает не обязательно из основного состояния свободного иона и поправки второго порядка теории возмущений к энергии становятся существенными.

Возбужденные орбитально-вырожденные термы расщепляются кристаллическим полем точно таким же образом, как и основной терм. В табл. 13.7 приведены все термы, возникающие из конфигураций (d)ⁿ. В табл. 13.8 указаны типы симметрии компонент, на которые расщепляются под действием октаэдрического кристаллического поля все термы, вплоть до 13-кратного вырожденного.

Таблица 13.7. Термы, возникающие из конфигураций (d)ⁿ. ²F (2) означает, что существуют два терма ²F

Таблица 13.8. Расщепление термов в октаэдрическом поле

Волновые функции и энергии компонент для каждого из этих термов можно найти по методу, описанному ранее для компонент терма ³F (d²), однако полученные результаты имеют смысл лишь в том случае, если Δ мало. Причину этого лучше всего иллюстрировать двумя примерами. Из конфигурации (d)⁵ возникают 16 термов, одиннадцать из которых являются дублетами (²I, ²Н, ²G (2), ²F (2), ²D (3), ²Р, ²S); под действием октаэдрического кристаллического поля они расщепляются и дают четыре ²A_1g-, три ²A_2g-, семь ²E_g-, восемь ²T_1g- и десять ²T_2g-уровней. В слабых полях основным является состояние ⁶A_1g, а в сильных полях - одно из состояний 2T_2g. Чтобы определить зависимость энергии уровня от Δ, очевидно, необходимо решить вековое уравнение из определителя десятого порядка и выбрать наименьший корень. К счастью, как будет видно, задача значительно упрощается, если Δ много больше, чем энергия межэлектронного отталкивания, что соответствует предельному случаю сильных полей. В более общем случае "промежуточных" полей проще всего провести интерполяцию результатов, полученных для слабых и сильных полей. Конфигурация (d)⁵ представляет особую трудность. Значительно проще исследование конфигурации (d)² и (d)⁸, так как в этих случаях с основным состоянием взаимодействует лишь один возбужденный уровень. Для этих конфигураций верхняя компонента основного терма (³F) свободного иона взаимодействует с одной из компонент возбужденного терма (³Р); обе компоненты обладают симметрией T_1g. Это влечет за собой важное для спектроскопии следствие, потому что обе компоненты близки по энергии. Рассмотрим подробнее конфигурацию (d)².

Обозначим два ³T_1g-уровня в соответствии с их генеалогией. В предыдущем рассмотрении комплексов слабых полей мы пренебрегали существованием возбужденного ³T_1g (³Р)-состояния. Поскольку терм ³Р не расщепляется в кристаллическом поле (см. табл. 13.8), энергия этого терма (нулевой порядок теории возмущений) не зависит от Δ. В то же время, так как термы ³T_1g (³F) и ³T_1g (³P) имеют одинаковую симметрию, отличен от нуля интеграл

который, как можно показать, следуя методу, изложенному на стр. 291-292, равен 2/5 Δ.

Теперь определим разность энергий двух термов в свободном ионе. Выраженная через параметры Слэтера - Кондона [соотношение (9.52)], она равна величине 15 F₂ - 75 F₄, которая будет фигурировать в уравнениях как параметр X. Принимая энергию ³F-терма свободного иона за нуль, получим следующую матрицу интегралов взаимодействия:

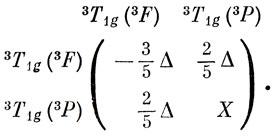
Корни векового уравнения

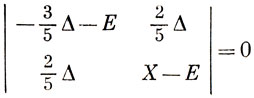
равны

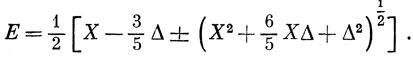
Для предельно слабых полей X >> Δ; разлагая в ряд по формуле бинома квадратный корень в уравнении (13.19) и ограничиваясь членами, линейными в Δ, имеем Е = X или Е = - 3/5 Δ. Этот результат получается и в том случае, если не учитывать взаимодействие между ³F- и ³Р-термами. Для предельно сильного поля Δ >> X; ограничиваясь только членами, линейными в X, получаем

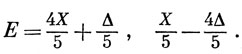
Рис. 13.7 дает картину расщепления ³F-терма, как и рис. 13,6,б, отличаясь от него учетом взаимодействия с ³Р-термом. Линии, показывающие зависимость ³T_1g-уровней от Δ, искривлены, и в пределе тангенсы угла наклона кривых равны - 4/5 для нижнего уровня и 1/5 - для верхнего. При достаточно большом Δ кривая ³A_2g-состояния пересекает верхнюю из кривых ³T_1g. Для иона V³⁺, где X - 13200 см^-1, такое пересечение имеет место при Δ = 11000 см^-1. Это обстоятельство будет существенным при обсуждении электронного спектра комплекса [V(H₂O)₆]³⁺.

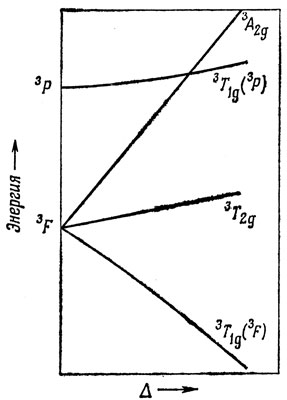
Рис. 13.7. Влияние взаимодействия второго порядка на основное состояние d²-октаэдрического комплекса

Комплексы сильных полей отличаются по спиновой мультиплетности от комплексов слабых полей, потому что энергия компоненты, относящейся к возбужденному терму свободного иона, быстро понижается с ростом Δ, пока в конце концов эта компонента не становится основным состоянием. Например, в конфигурации (d)⁵ компонента ²T_2g (²D) заменяет ⁶A_1g в качестве основного состояния. Эта последняя представляется кривой с нулевым наклоном (будучи единственной компонентой орбитально невырожденного терма ⁶S), в то время как первая имеет тангенс угла наклона кривой, равный -2. В случае предельно сильного поля уже нельзя больше строить волновые функции на основе рассмотрения термов свободного иона, а надо исходить из конфигураций, возникающих при действии кристаллического поля на d-орбитали (см. табл. 13.5). В этом предельном случае уровень ²T_2g (²D) соответствует конфигурации t_2g⁵; на одной из t_2g-орбиталей имеем дырку. Можно получить зависимость энергии этого уровня от Δ, если каждому электрону на t_2g-орбиталях приписать энергию -

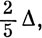
т. е.

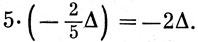
Аналогичное рассмотрение можно провести для всех других состояний в сильном поле, как основного, так и возбужденных. Например, из конфигурации (d)¹ получается соответствующая основному состоянию конфигурация (t_2g)⁶(e_g)¹, и энергия выражается через Δ следующим образом

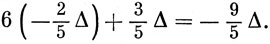
Таким же образом тангенс угла наклона кривой, соответствующей основному состоянию конфигурации (d)², равен -

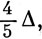
что равно предельному значению, полученному ранее [см. выражение (13.20)]. В качестве примера построения волновой функции в случае предельно сильного поля снова возьмем (t_2g)². Основным состоянием будет ³T_1g. Если рассмотреть компоненту с M_s = 1, то при этом спиновом ограничении возможны лишь три способа распределения электронов по трем орбиталям, которые должны давать три пространственные компоненты T_1g-состояния. Можно записать их в виде

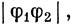
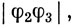
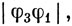
где φ₁, φ₂, φ₃ - любые три независимые функции для t_2g-орбиталей, т. е. d_xy, d_yz и d_zx или (2, 1), (2, -1)

и

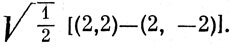
Следуя методу, описанному в этом и следующем разделах, можно построить энергетические диаграммы для всевозможных конфигураций d-электронов в кристаллическом поле. Два типичных случая приведены на рис. 13.8 и 13.9 ^*).

^*) (Другие случаи рассмотрены в книге [31].)

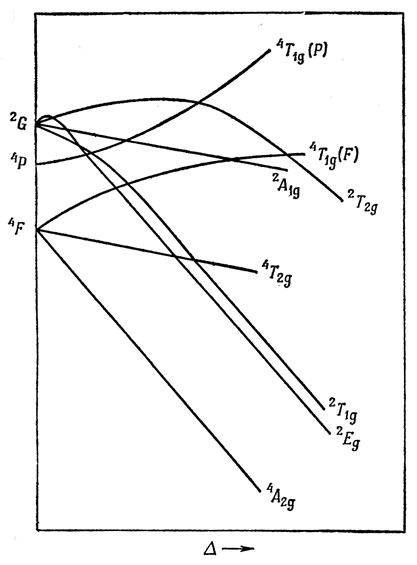
Рис. 13.8. Энергетическая диаграмма для конфигурации d³ в кристаллическом поле

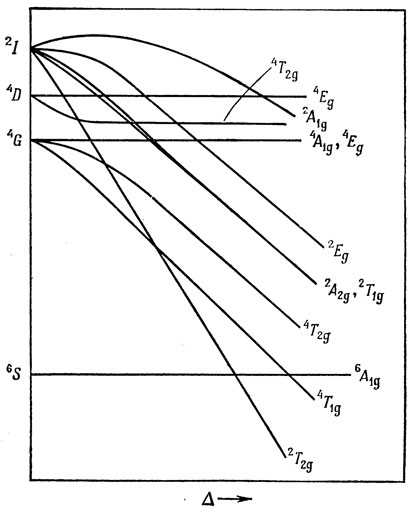
Рис. 13.9. Энергетическая диаграмма для конфигурации d⁵ в кристаллическом поле