
Глава 13
13.1. Ион Fe3+ имеет пять 3d-электронов. Основным состоянием октаэдрического комплекса является состояние 6A1g (слабое поле) или состояние 2T2g (сильное поле). Поскольку ион является бесцветным, очевидно, не существует низко расположенных электронных состояний, в которые возможны оптические переходы из основного состояния. Из рис. 13.9 можно видеть, что если 2T2g было бы основным состоянием, то существовали бы другие низко расположенные дублетные состояния и при переходе в некоторые из них можно было бы ожидать поглощения видимого света. Это были бы запрещенные g - g-переходы, но, как уже говорилось в разд. 13.8, это не очень строгое правило отбора. С другой стороны, если состояние 6A1g-основное, то единственным низко расположенным состоянием является секстетное, и, следовательно, все наиболее длинноволновые переходы были бы запрещены по спину, так же, как g - g-переходы. Исходя из положения иона F- в спектрохимическом ряду, можно ожидать, что он образует комплексы слабых полей.
13.2. Характер, соответствующий операции поворота на угол α, равен [см. выражение (13.4)]
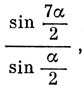
поэтому, например,
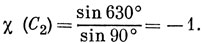
Аналогично χ (С3) = 1, χ (С4) = - 1. Поскольку d-орбитали симметричны относительно инверсии, χ (i) = 7. Для того чтобы доказать, что расщепление происходит на компоненты T1g, T2g, A2g, достаточно воспользоваться приведенным ниже набором характеров:

13.3. Конфигурация d9 свободного атома дает терм 2D. В октаэдрическом поле основным состоянием этого терма является 2Eg, которое (см. табл. 13.5) описывается волновыми функциями
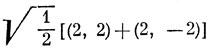
Это состояние соответствует конфигурации (t2g)6 (eg)3, а в качестве его собственной функции, записанной в виде слэтеровского определителя, можно было взять, например,
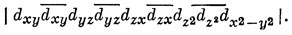
Конфигурация d8 свободного атома дает в основном состоянии терм 3F. В октаэдрическом поле основным состоянием этого терма является 3A2g, а соответствующая волновая функция (см. табл. 13.6) имеет вид
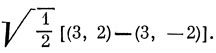
В сильном поле d-орбитальная конфигурация для этого состояния есть (t2g)6 (eg)2, и одна из компонент триплетного состояния может описываться функцией
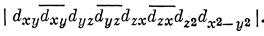
13.4.
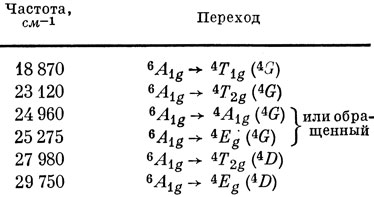
(см. работу [87]).
13.5. Интегралы взаимодействия можно взять из матрицы (13.9). Единственным отличным от нуля недиагональным элементом матрицы является интеграл, вычисленный с функциями (2, 2) и (2, -2), откуда следует, что все интегралы взаимодействия, рассчитанные с различными функциями 3Р-состояния, обращаются в нуль. Вычислим энергию кристаллического поля с первой из собственных функций (МL = 1):
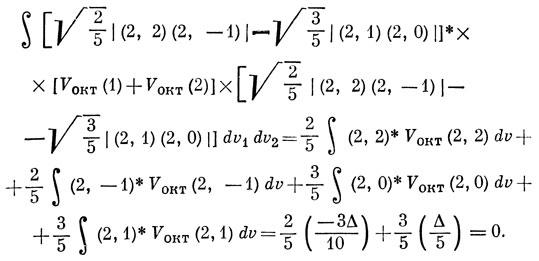
13.6. Обозначим орбитали, как это сделано на рис. 19.2 в указаниях к решениям задач, и рассмотрим поведение Az.

Складываем: 4 (Az - Ex + Fx - Cz)
Нормируем: ψ1 (t2g) = 1/2 (Az - Ex - Cz + Fx).
Другие компоненты в силу симметрии имеют вид
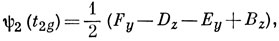
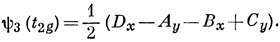
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'